基于Hilbert空间有界线性算子方程等价性的研究

范大付

(百色学院 教务处, 广西 百色 533000)



基于Hilbert空间有界线性算子方程等价性的研究

范大付

(百色学院 教务处, 广西 百色 533000)

摘要:有界线性算子方程解的性质在计算中是十分必要的.在Hilbert空间上,研究有界线性算子解的等价性.将该系统变得更加简单更加便于求解.通过算子的分块技术,将算子分成等价形式,且利用Moore-Penrose 逆来表示,最终给出了线性算子方程的一些简单等价形式.

关键词:Hilbert空间; 算子方程; Moore-Penrose逆

设H、K为Hilbert空间,且H(H,K)表示所有由H到K的有界线性算子的集合.当H=K时,H(H)=H(H,K).对于有界线性算子A∈H(H,K),R(A)和N(A)分别表示A的值域和零空间.设A*表示算子A的共轭转置.设I和0分别表示单位算子和零算子.对于有界线性算子A∈H(H,K)且R(A)是闭的,存在唯一有界线性算子X∈H(K,H)满足:

AXA=A,XAX=X,

则X称为A的Moore-Penrose逆,表示为X=A†(见文献[1]).

近年来,Hilbert空间上的算子方程的研究已经被国内外许多研究学者关注和研究.文献[2-6]研究了有限维下著名的Sylvester方程AX-AX=0的解.文献[7-8]研究了更一般的Sylvester方程.文献[9]研究了方程AX+AXT=0的解以及在轨迹理论上的应用.文献[10-11]将矩阵方程ATX+XTA=B推广到无限维空间H(H此时表示希尔伯特空间)上的算子方程A*X+X*A=B,且讨论了当算子A的值域是闭时给出了方程有解的充要条件.文献[12]研究了算子方程(A*)nX+X*An=B的解.文献[13]研究了混合的Sylvester方程的可解性条件和广义解.文献[14]研究了耦合的广义Sylvester矩阵方程.文献[15-18]研究了在Hilbert C*-模上自伴算子方程的解.

本文研究Hilbert空间上有界线性算子方程等价性.利用算子的分块技术和Moore-Penrose逆,给出算子方程的齐次的等价形式,这样使得算子方程更简单且更适合求解.给出下面2类方程的等价形式:

(i) 设A∈H(H,K)和C,X,Y∈H(K,H).若CAA†=A†AC,B=B*,给出

(1)

的等价形式.

(ii) 设A,C∈H(H,K)和R(A)是闭的,且X,Y∈H(K).若CAA†=A†AC和B=B*,给出

(2)

的等价形式.

引理 1[1]若A∈H(H,K)且R(A)是闭的,则A表示为

(3)

其中A1是可逆的,进一步,A†存在,且可表示为

(4)

1主要结论

基于Hilbert空间研究有界线性算子方程等价形式.主要推导了方程(1)和(2)的特殊的等价形式,以便得到更适合实际应用的形式.

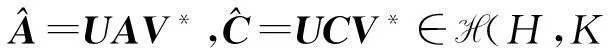
(5)

由(5)式,则

(6)

2) 设F:(X,Y)|→(UXU-1,VYV-1).由于U、V非奇异,则F是满射的且单射的.显然,F为(X,Y)和(UXU-1,VYV-1)间的一个同构映射.

推论 1若定理1中H=K和U=V,则:

定理 2设A∈H(H,K)和C,X,Y∈H(K,H)满足方程(1).设R(A)是闭的,且CAA†=A†AC,B=B*.若存在Q∈H(K,K)使得Y=XQ,则方程(1)的解等价于

(7)

证明设空间H、K的分块分别为:

(8)

因为R(A)闭的和由引理1,则

(9)

由引理1,则A是Moore-Penrose可逆的且

由(9)式且CAA†=A†AC,则C、B的分块为:

(10)

同理,将X、Y分别表示为:

(11)

将(9)～(11)式代入方程(1),则

(12)

同时

(13)

由B=B*,以及(12)和(13)式,则

(14)

和

(15)

由(14)和(15)式,所以

(16)

若存在

使得

则(16)式可写为

进一步有

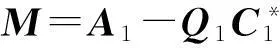
(17)

由(17)式得

定理 3设A∈H(H,K)和C,X,Y∈H(K,H)满足方程(1)和R(A)是闭的,且CAA†=A†AC,B=-B*.若存在Q∈H(K,K)使得Y=XQ,则方程(1)的解等价于

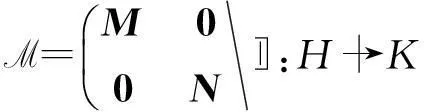
证明由B=-B*,以及(12)和(13)式,则

(18)

和

(19)

由(18)和(19)式,则

(20)

则(20)式等价于

进一步有

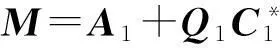
(21)

由(21)式得

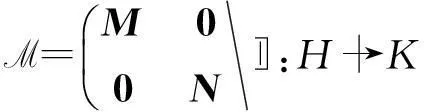
定理 4设A,C∈H(H,K)和X,Y∈H(K)满足(2)式,若R(A)是闭的且CAA†=A†AC和B=B*,则(2)式等价于

其中

证明因为R(A)是闭的和引理1,则A†存在且有分块为

(22)

由CA†A=AA†C,则

(23)

同理有

(24)

将(22)～(24)式代入方程(2),则

(25)

因此

(26)

由(25)和(26)式,则

和

进一步,分别得

其中

由B=B*,则

因此有

和

其中

定理 5若定理4中B=-B*,则方程(2)的解等价于

其中

2例

下面给出定理2的一个数值算例.

例 1设方程(1)中

和

则方程(1)有解:

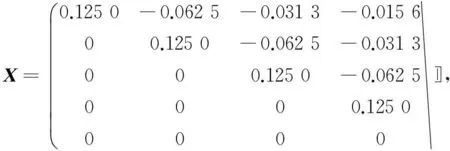
另外,设

和

可验证:Y=XQ且‖XM-M*X*‖∞=0.001 7.反之,可验证‖XA+CA-B‖∞=0.005 5.因此,可知(X,Y)满足方程(1)当且仅当X满足方程(7).

参考文献

[2] REHMAN A, WANG Q W, HE Z H. Solution to a system of real quaternion matrix equations encompassingη-Hermicity[J]. Appl Math Comput,2015,265:945-957.

[3] FERNANDO D T. The solution of the equation AX+BX*=0[J]. Linear Multilinear Algebra,2013,61(12):1605-1628.

[4] FERNANDO D T, DOPICO F M, GUILLERY N, et al. The solution of the equation AX+X*B=0[J]. Linear Algebra Appl,2013,438(7):2817-2860.

[5] GARCIA S R, SHOEMAKER L. On the matrix equation XA+AXT=0[J]. Linear Algebra Appl,2013,438(6):2740-2746.

[6] CHAN A, GERMAN L, GARCIA A, et al. On the matrix equation XA+AXT=0(II):type 0-iinteractions[J]. Linear Algebra Appl,2013,439(12):3934-3944.

[7] HUANG L J, WANG Q W, ZHANG Y. The Moore-Penrose inverses of matrices over quaternion polynomial rings[J]. Linear Algebra Appl,2015,475:45-61.

[8] ZHOU B, LAN J, DUAN G R. Toward solution of matrix equation X=Af(X)B+C[J]. Linear Algebra Appl,2011,435(6):1370-1398.

[9] FERNANDO D T, DOPICO F M. The solution of the equation XA+AXT=0 and its application to the theory of orbits[J]. Linear Algebra Appl,2011,434(1):44-67.

[10] DRAGAN S D. Explicit solution of the operator equation A*X+X*A=B[J]. J Comput Appl Math,2007,200(2):701-704.

[11] DRAGANA S C. The solutions of some operator equations[J]. J Korean Math Soc,2008,45(5):1417-1425.

[12] TIAN X G, WANG S Y. Positive and real-positive solutions of the operator equation AX-XA*=B[J]. Pure Appl Math,2010,26(6):1047-1052.

[13] WANG Q W, HE Z H. Solvability conditions and general solution for mixed Sylvester equations[J]. Automatica J IFAC,2013,49(9):2713-2719.

[14] WANG Q W, HE Z H. Systems of coupled generalized Sylvester matrix equations[J]. Automatica J IFAC,2014,50(11):2840-2844.

[15] DONG C Z, WANG Q W, ZHANG Y P. The common positive solution to adjointable operator equations with an application[J]. J Math Anal Appl,2012,396(2):670-679.

[16] SONG G J. Common solutions to some operator equations over HilbertC*-modulesandapplications[J].LinearMultilinearAlgebra,2014,62(7):895-912.

[17]SONGGJ,WANGQW.PositiveandrepositivesolutionstosomesystemsofadjointableoperatorequationsoverHilbertC*-modules[J].ElectronJLinearAlgebra,2011,22:1070-1084.

[18]WANGQW,DONGCZ.ThegeneralsolutiontoasystemofadjointableoperatorequationsoverHilbertC*-modules[J].OperMatrices,2011,5(2):333-350.

[19] 范大付.Banach空间上算子方程的解[J]. 山东大学学报(理学版),2013,48(2):105-110.

2010 MSC:15A09; 47L30

(编辑余毅)

Research on Equivalence of the Solutions for the Operators Equation over Hilbert Space

FAN Dafu

(Dean’sOffice,BaiseCollege,Baise533000,Guangxi)

Abstract:The properties of boundary linear operator equations are very necessary in scientific computation of the linear systems. Based on Hilbert space, we consider the equivalence of the solutions for the linear bounded operator systems. The systems are written into a simple and equivalent systems. The main advantage is that the systems can be solved easily. By introducing the block technology of operator, the operator can be written into an equivalent form. Finally, we present some simple equivalent expression form of the linear bounded operator systems by using Moore-Penrose inverse.

Key words:Hilbert Space; the operator equation; the Moore-Penrose inverse

doi:10.3969/j.issn.1001-8395.2016.01.021

中图分类号:O151

文献标志码:A

文章编号:1001-8395(2016)01-0117-06

作者简介:范大付(1974—),男,讲师,主要从事基础数学、概率与统计的研究,E-mail:459990654@qq.com

基金项目:广西高校科学技术研究项目(2013LX146)、广西自然科学基金(2014GXNSFAA118030)和广西高等教育本科教学改革工程项目(2015JGZ160、2015JGB376)

收稿日期:2015-06-01