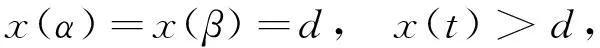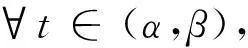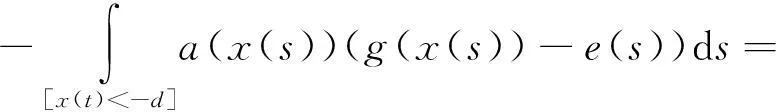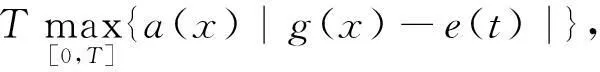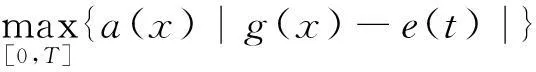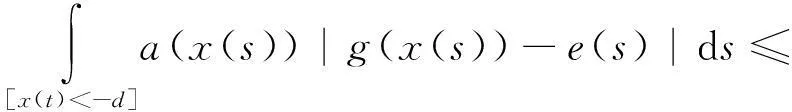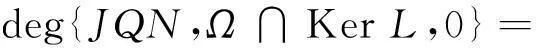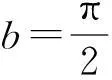具有强迫项的有限时滞Lienard方程周期解的存在性
黄 勇, 黄燕革
(百色学院 数学与计算机信息工程系, 广西 百色 533000)
具有强迫项的有限时滞Lienard方程周期解的存在性
黄勇,黄燕革
(百色学院 数学与计算机信息工程系, 广西 百色 533000)
摘要:利用Mawhin延拓定理证明,构造新算子,使用新技巧,研究了一类具有强迫项和有限时滞的二阶Lienard方程
的周期解问题,得到了方程至少存在一个周期解的充分条件,获得了新的结论.
关键词:强迫项; 时滞; Lienard方程; 周期解; Mawhin延拓定理
关于具有有限时滞Lienard方程
(1)
和关于具有强迫项的Lienard方程
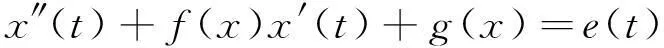
(2)
的周期解的存在性的研究已有许多(参见文献[1-22]及其参考文献).据我们所知,研究同时具有强迫项和有限时滞的Lienard方程周期解的存在性还不多见.
本文研究如下一类同时具有强迫项和有限时滞Lienard方程
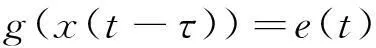
(3)
的周期解的存在性问题,其中,f1(x)、f2(x)和g(x)是定义在R=(-∞,+∞)上的连续实函数,常数τ≥0,e(t)是周期为T的连续函数,即对于常数T>0,e(t+T)=e(t).利用Mawhin延拓定理给出方程(3)存在周期解的一些充分条件.
1假设与引理
为研究方便,把方程(3)转化为以下等价方程组
(4)
其中
常数τ≥0.
这样,研究方程(3)就转化为研究方程(4).为利用Mawhin延拓定理[23],考虑Banach空间Z中的算子方程

(Eλ)
其中,L:domL∩Z→Z是一个线性算子,N:Z→Z是一个连续的算子和λ∈[0,1]是一个参数.
相应于方程(Eλ)有
因此,关于方程组(4)的周期解的存在性问题被转化为当λ=1时,方程组(5)在Z中的周期解的存在性问题.
如果
dim KerL=codim ImL<+∞,
并且ImL在Z中闭,则算子L称为指标为零的Fredholm算子[24].
如果L为指标为零的Fredholm算子,则存在连续投影算子P、Q分别为:
P:Z∩domL→KerL,
Q:Z→Z/ImL,
且有
ImP=KerL,KerQ=ImL.
因此有
L|dom L∩Ker P:domL∩KerP→ImL
是一个一一映射且具有连续广义逆kp及
J:Z/ImL→KerL
是一个同构.
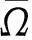
1)LX≠λNX,∀X∈∂Ω∩domL,λ∈(0,1),
2)QNX≠0,∀X∈∂Ω∩KerL,
3) deg{JQN,Ω∩KerL,0}≠0;
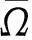
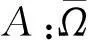
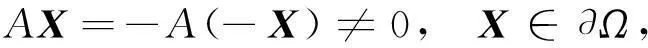
则
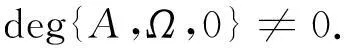
为了讨论方程(4)的周期解存在性问题,记
并在Z中定义范数
其中
易证,在此范数下Z为Banach空间.定义
易证
dim KerL=codim ImL=2
且ImL为Z的闭子空间,故知L为指标为零的Fredholm算子.
2主要结果
定理假设f1(x)、f2(x)和g(x)是定义在R=(-∞,+∞)上的连续实函数,e(t)是周期为T的连续函数,并且以下条件成立:
(A1)f2(x)在R上有界,存在常数b>0,使

(A3)f1(x)>0,且
则方程组(4)至少存在一个周期为T的周期解.
证明第1步:证明当λ∈(0,1)时,对于方程(5)的任意一个T周期解
一定存在正数M>0,使得对所有的t∈[0,T]有
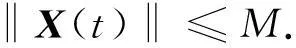
先证明第一个分量x(t)≤M1,常数M1>0.由(5)式的第2个方程积分得
(6)
由假设条件(A1)和(A2)可以确定必存在t0∈[0,T],使得
(7)
现记

以下证明存在M1>0,使x(t*) 事实上,如果x(t*)≤d,取M1>d,结论显然成立.若x(t*)>d,结合(7)式知存在包含t*的区间[α,β],这里α=α(x,λ),β=β(x,λ),且β-α (8) (9) (10) 这样由(5)式的第一个方程及(9)式得 (11) 从而存在ξ∈[α,β],使 (12) 现记|u|q表示Lq([α,β],R)中的范数,其中1≤q<+∞,即 可得 (13) 将方程(5)的第1个方程写为 得到 (14) 另一方面有 (15) 代入(15)式得到 其中,k为满足0 将(14)同(15)及(16)式相比较,分别得到 和 由条件(A3)知道,无论上述哪种情况,均存在常数c2>0,使得 从而 (19) 令 则c3是独立于x,λ的常数,让M1≥c3,这样已经证明了存在常数M1≥0,使 从而第1个分量 下面证明,在上述前提下,第2个分量y(t)≤M2,常数M2>0,且存在常数M>0,使 事实上,由条件(A1)、(A2),可以得到 其中-d≤x≤M1.由于 为一个常数,令 则 因此由(5)式的第2个方程有 则由(12)式和x(t*)的做法,容易得到 (21) 即证明了存在正数M2>0,M2=c1+2c4,使第2个分量 用x′(t)乘以(5)式的第1个方程,并在[0,T]上积分得 即 故 (22) 因此,由(7)和(22)式得 (23) 均有‖X(t)‖≤M. 第2步:为利用引理1,记 L:domL∩Z→Z是一个线性算子,N:Z→Z是一个连续的算子,则L为指标为零的Fredholm算子,在前面范数规定下Z为Banach空间.定义连续投影算子P、Q为 则有 ImP=KerL,KerQ=ImL, 且 L|dom L∩Ker P:domL∩KerP→ImL 是一个一一映射且具有连续广义逆kp及Z/ImL→KerL是一个同构,记为J.kp由下式给出 根据以上证明,显然Ω满足引理1中的条件1)的要求. 现在设 则X是一个在R2中的常矢且‖X‖=M.如果|x|>d,由条件(A2)、(19)和(22)式获得 如果|x|≤d,由 有 得到 因此,无论哪种情况都有 (24) 这样,引理1中的条件2)满足. 现定义连续算子B:Ω→Ω,BX=(y,-x)T,根据Ω定义,Ω关于原点对称,且当X=(x,y)T∈∂Ω∩KerL时, 由引理2有 deg{B,Ω∩KerL,0}≠0. 作一个函数 φ(X,u)=uBX+(1-u)QNX= 引理1中的条件3)满足. 这样,Ω满足引理1的全部条件.故由引理1,算子方程LX=NX在Banach空间Z至少有一个解.这样我们已经证明方程组(4)至少存在一个T周期解.定理证毕. 3应用举例 考虑方程 (25) 因为 参考文献 [1] HERDEN U A. Periodic solutions of a nonlinear second order differential equations with delay[J]. J Math Anal Appl,1979,70:599-609. [2] HALE J K. Theory of Functional Differential Equations[M]. New York:Springer-Verlag,1977:5-25. [3] HALE J K. Introduction to Functional Differential Equations[M]. Berlin:Springer-Verlag,1977:11-30. [4] KUANG Y. Delay Differential Equations with Applications in Population Dynamics[M]. New York:Academic Press,1993:8-16. [5] LIAO X X . Theory and Application of Stability for Dynamical Systems[M]. Beijing:Defence Industrial Press,2000:35-46. [6] 魏俊杰,黄启昌. 关于具有限时滞Lienard方程周期解的存在性[J]. 科学通报,1997,42(9):906-909. [7] 陈红斌,李开泰,李东升. Lienard方程周期解的存在唯一与唯二性问题[J]. 数学学报,2004,47(3):417-424. [8] 陈世哲,陈仕洲. 具有两个偏差变元的Lienard型方程的周期解的存在唯一性[J]. 科技通报,2012,28(11):11-15. [9] 陈仕洲. 一类Lienard型p-Laplacian方程周期解的存在唯一性[J]. 数学的实践与认识,2013,43(8):244-253. [10] 陈月红. 具有两个偏差变元的Lienard型方程周期解的存在性[J]. 数学的实践与认识,2014,44(18):315-320. [11] 邓伟,蒲志林. 一类中立型 Duffing 方程的周期解[J]. 四川师范大学学报(自然科学版),2012,35(5):585-588. [12] 董宁青,安天庆,艾孜玛洪·努尔别克. 二阶非自治(q,p)-Laplace方程周期解的存在性[J]. 四川师范大学学报(自然科学版),2012,35(5):607-609. [13] 汪小明. 一类具时滞高阶泛函微分方程的周期解[J]. 四川师范大学学报(自然科学版),2014,37(4):519-523. [14] 张莉,黄先开,葛渭高. 一类中立型泛函微分方程周期解的存在性[J]. 北京理工大学学报,2011,31(12):1489-1492. [15] 程志波,向上.P-laplacian类Dufing方程正周期解的存在性与唯一性[J]. 郑州大学学报(理学版),2013,45(2):1-5. [16] 黄勇,姚晓洁,秦发金. 一类二阶微分方程周期解的存在性和唯一性[J]. 广西民族大学学报(自然科学版),2014,20(4):46-53. [17] 田德生. 三阶常系数拟线性泛函微分方程的周期解[J]. 纯粹数学与应用数学,2013,29(3):233-240. [18] 陈新一. 具偏差变元高阶泛函微分方程周期解的存在定理[J]. 西北民族大学学报(自然科学版),2013,34(90):1-7. [19] 陈新一. 高阶非线性中立型泛函微分方程周期解的存在性[J]. 山东大学学报(理学版),2011,46(8):47-51. [20] 殷雪剑,路召飞. 二阶时滞微分方程周期解的存在唯一性及数值解法[J]. 重庆工商大学学报(自然科学版),2011,28(4):334-338. [21] 韦煜明,王勇,唐艳秋. 具P-laplacian算子时滞微分方程边值问题解的存在唯一性[J]. 广西师范大学学报(自然科学版),2012,30(2):48-53. [22] 陈楷城. 二阶非线性中立型泛函微分方程周期解的存在性[J]. 数学的实践与认识,2014,44(3):268-273. [23] GAINES R E, MAWHIN J L. Coincidence Degree and Nonlinear Differential Equations[M]. Berlin:Springer-Verlag,1977:6-12. [24] DEIMLING K. Nonlinear Functional Analysis[M]. Berlin:Springer-Verlag,1985:21-33. [25] OMARI P, VILLARI G, ZANOLIN F. Periodic solutions of the Lienard equation with one-side growth restrictions[J]. J Diff Eqns,1987,67:278-293. 2010 MSC:34C25 (编辑余毅) The Existence of Periodic Solutions for a Class of Forced and Finite Delayed Lienard Equations HUANG Yong,HUANG Yan’ge (DepartmentofMathematicsandComputerInformationTechnology,BaiseCollege,Baise533000,Guangxi) Abstract:In this paper, a new operator is constructed by using the Mawhin’s continuity theorem. The periodic solutions to a class of forced and finite delayed second-order Lienard equations of the form x″(t)+f1(x)x′(t)+f2(x)(x′(t))2+g(x(t-τ))=e(t) are studied. Some sufficient conditions for the existence of periodic solutions are given. Key words:forced; delayed; Lienard equations; periodic solution; Mawhin’s continuity theorem doi:10.3969/j.issn.1001-8395.2016.01.020 中图分类号:O157.6 文献标志码:A 文章编号:1001-8395(2016)01-0111-06 作者简介:黄勇(1961—),男,教授,主要从事微分方程的研究,E-mail:huangyong861@sohu.com 基金项目:广西自然科学基金(2013GXNSFAA019022)和广西高校科研项目基金(2013YB243) 收稿日期:2015-05-12