具有临界指数和Robin边界的Kirchhoff方程解的存在性

杨　婧,　蒲志林*，　奉　卫

(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066;　2. 内江师范学院 数学与信息科学学院, 四川 内江 641100)



具有临界指数和Robin边界的Kirchhoff方程解的存在性

杨婧1,蒲志林1*，奉卫2

(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066;2. 内江师范学院 数学与信息科学学院, 四川 内江 641100)

摘要：主要研究带有非线性边界耗散和临界指数的Kirchhoff 方程在t→∞ 时的渐进性态,证明弱解的存在性.首先,利用极大单调算子的理论证明局部解的存在唯一性,其次用能量等式证明全局解的存在性并给出其变分形式.

关键词：Robin边界条件; 临界指数; 极大单调算子; 解的存在性; 能量等式; 变分形式

1预备知识

1.1Kirchhoff方程的起源及研究进展考虑带有非线性阻尼的Kirchhoff波方程

(1)

其中,u=(u1,u2,…,uN)=u(t,x)是一个向量,N≥1.Ω为Rn上的有界区域,M为函数M(λ)=a+bγλγ-1,λ≥0,a,b≥0,a+b>0,γ>1.

对于方程(1),当a>0,b≥0为非退化;当a=0,b>0,为退化;当a>0,b=0,则方程为通常所说的半线性波方程[1].

方程(1)起源于对微小振幅的弹性细绳振动的精确研究[2].实际上对于长度L>0的弹性细绳振动的数学模型的原始方程为

(2)

其中,u(x,t)=u是空间坐标x与时间t的横向位移,E是Young系数,ρ是细绳的密度,h是振动高度,L为长度,ρ0为初始轴向拉力,δ是阻尼系数,f是外力.当δ=f=0时,Kirchhoff是第一个在研究弹性细绳振动时引入方程(2)的数学家,因此在他以后的这类波方程被称为Kirchhoff方程.Kirchhoff方程在数学物理的许多领域都有重要的意义,对于Kirchhoff波方程的研究已经有大量的文章,文献[3-4]研究了方程

在边界条件

全局解的存在性和指数衰减的问题.文献[5]研究了方程

在Dirichlet边界条件下时全局吸引子的问题.对于Robin边界条件下的半线性波方程

文献[6]研究其弱解的存在性及渐近收敛于一个全局的紧致吸引子.还有不少研究退化的Kirchhoff型方程[7]

在Dirichlet边界条件下时弱解存在性的问题,而非线性退化的Kirchhoff型方程[8]

在Dirichlet边界条件下时局部解存在性的问题也有人探讨过.但据我们所知,对于非退化Kirchhoff型波方程在Robin边界条件下解的存在性问题研究相对较少,本文将研究这一问题.

1.2本文的主要工作在已有文献的基础上,探讨带有Robin边界条件的非退化Kirchhoff波方程解的存在性问题,具体考虑如下非退化具有非线性边界阻尼的Kirchhoff波方程的初边值问题

(3)

其中,Ω⊂R3为有界开集并具有光滑的边界Γ,u=u(x,t)是Ω×[0,∞)上的实值函数,边界Γ的单位外法向量为v,∂vu为外法向导函数,而f、g为非线性函数,本文主要讨论非退化的情形,即:M=M(λ)=a+bγλγ-1,λ≥0,a>0,b≥0,a+b>0,γ>1.

1.3函数空间记号令H=L2(Ω),范数为

令V=H1(Ω),其内积为

范数为

其中

令Wm,p(Ω)={u∈Lp(Ω),Dαu∈Lp(Ω),0≤|α|≤m}范数为

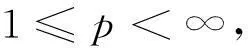
H的对偶空间为H*,V的对偶空间为V*=H-1(Ω),

令

1.4极大单调算子理论的一些结果

定义 1[9]设H是一个Hilbert空间,令B,B1,B2:H→H是非线性算子,有序关系B2≤B≤B1是指满足下列关系

(4)

定义 2设H是一个Hilbert空间,算子B:H→H,单调指满足下列关系

(Bu-Bv,u-v)≥0,

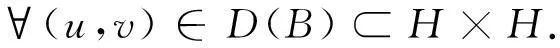
定义 3设H是一个Hilbert空间,算子B:H→H,极大单调指:对∀(x,y)∈H1(Ω)×(H1(Ω)′),若(x-u,y-Bu)≥0,u∈D(B),则必有x∈D(B)且y=Bx.

若B、B1、B2满足(4)式且B1、B2是极大单调算子,则B也是极大单调的.事实上,若B1、B2是极大单调算子,由定义3知:∀(x,y)∈H1(Ω)×(H1(Ω))′.若(x-u1,y-B1u1)≥0,u1∈D(B1),则x∈D(B1)且y=B1x.若(x-u2,y-B2u2)≥0,u2∈D(B2),则x∈D(B2)且y=B2x.

由定义1知:B2≤B≤B1则令

设(x-u,y-Bu)≥0,u∈D(B)有

即

则有

则可知B是极大单调算子.

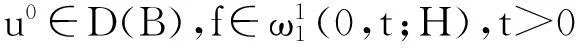
2主要结果及其证明

考虑方程组(3),对f、g、M做如下的假设:

1) 增长限制性条件:对所有的s有f∈C2(R),且|f′(s)|≤c(1+|s|);

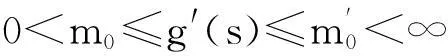
5) g(0)=0;

下面先对非线性函数g进行一些讨论.

对s≥2R,运用假设4)和5)有:令k:0～s,μ:0～1,则k=μs,dk=sdμ.

同样地,对于s∈(-2R,-ζ)有类似的结论.将这些式子合并在一起得到

(5)

同样的方法,可得

有

(6)

叙述并证明本文的主要结果[11-13].

定理 1假设(u0,u1)∈H满足初值条件,则方程组(3)存在惟一的弱解(u,ut)∈C([0,∞);H),并有以下的性质:

1) 有界正则性

(7)

2) 弱解满足能量恒等式

(8)

3) 对所有的v∈H1(Ω),弱解满足下列的变分不等式

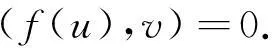
(9)

定理 2假设u0∈H2(Ω),u1∈H1(Ω),并且u0,u1在边界Γ上满足:∂vu0+u0+g(u1)=0且在原有的假设下有这个弱解是“强”的,且满足下列的性质

步骤 1局部解的存在惟一性.

(10)

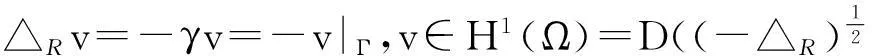
令

则有

同样地,令

则有

令

则有

对所有的(uj,vj)∈D(B1),j=1,2,令:u1-u2≥0,v1-v2≥0,则有

由假设4)知

即B1是单调算子,同理可得B2也是单调算子.

令

则有

即有

将u=v+h1代入v-△R(m1u+Rg(γv))=h2得

h2+△Rm1h1.

令

又由于映射I:H1(Ω)→(H1(Ω))′是有界、半连续、单调的.则I+B1是极大单调算子[12],那么B1就为极大单调算子.同理可证得B2也为极大单调算子.以上的证明是参照参考文献[6]得来的,证得B为极大单调算子.

方程组(3)用算子理论可描述为

(11)

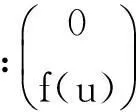
步骤 2全局解、能量恒等式、变分形式.先将方程(3)两边乘以ut积分得

再积分得

令线性能量泛函为

(12)

非线性能量泛函为

则有

(13)

又由于弱解是强解的极限,令

其中,t∈(0,tmax),且un→u在c([0,t];H),则在t∈(0,tmax)上强解可有

(14)

自然当un→u在c([0,t];H)上也有此结果.

由嵌入定理可知H1(Ω)⊂Lq(Ω),其中2≤q≤6.又对∫ΩF(u)有

而

则存在常数C=C(E(u(t)))使得

(15)

由假设2)知

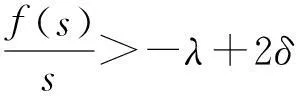
其中

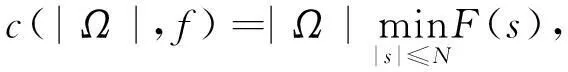
所以有

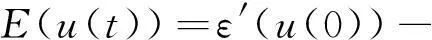
因为

则有

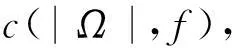
其中

可得

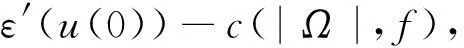
说明在任意时间线性能量方程有界,且依赖于初始能量、Ω的测度及f,即全局解是存在的.以上证明参照文献[6]得来.

现计算其变分形式.将方程组(3)与φ∈H1(Ω)内积得

即

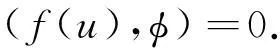
参考文献

[1] GIUSEPPINA A, PATRIZIA P, MARIA C S. Asymptotic stability for nonlinear kirchhoff systems[J]. Nonlinear Analysis(Real World Appl),2009,10:889-909.

[2] NISHIHARA K. Nonlinear vibration of an elastic sting[J]. J Sound Vibration,1968,8:134-146.

[3] MATSUYAMA T, IIERATA R. On global solutions and energy decay for the wave equations of Kirchhoff type with nonlinear damping terms[J]. J Math Anal Appl,1996,204:729-753.

[4] NISHIHARA K. Exponentially decay of solutions of some quasilinear hyperbolic equations with linear damping[J]. Nonlinear Anal(TMA),1984,8(6):623-636.

[5] 杨志坚,程建玲. Kirchhoff型方程解的渐进行为 [J]. 数学物理学报,2011,A31(4):1008-1021.

[6] IGOR C, MATTHIAS E, IRENA L. On the attractor for a semilinear wave equation with critical exponent and nonlinear boundary dissipation[J]. Commun Partial Diff Eqns,2002,27(9/10):1901-1951.

[7] TOKIO M. On global solutions and energy decay for the wave equations of kirchhoff type with nonlinear damping terms[J]. J Math Anal Appl,1996,5:712-729.

[8] TAKESHI T. Existence and asymptotic behaviour of solutions to weakly damped wave equations of Kirchhoff type with nonlinear damping and source terms[J]. J Math Anal Appl,2010,361:566-578.

[9] LASIECKA I, TRIGGIANI R. Control Theory for Partial Differential Equations:Continuous and Approximation Theorems, I.Abstract Parabolic Systems[M]. Cambridge:Cambridge University Press,2000.

[10] SHOWALTER R. Monotone operator in Banach Spaces and Nonlinear Partial Differential Equations[M]. Providence:Amer Math Society,1997.

[11] LASIECKA I, TRIGGIANI D. Uniform stabilization of a semilinear wave equation with nonlinear boundary dissipation[J]. Diff Integral Eqns,1993,6:507-533.

[12] BARBU V. Nonlinear Semigroups and Differential Equations in Banach Space[M]. Providence:Am Math Society,1976.

[13] BREZIS H. Operateurs Maximaux Monotones[M]. North-Holland:Amsterdam,1973.

[14] HALE J. Asymptotic Behavior of Dissipative systems[M]. Providence:Am Math Society,1988.

[15] FAVINI A, HORN M, LASIECKA I, et al. Global existence, uniqueness and regularity of solutions to a von Karman system with nonliear boundary dissipation[J]. Diff Integral Eqns,1996,9:267-294.

2010 MSC：35B33; 35G60

(编辑郑月蓉)

On the Existence for the Solution of Kirchhoff Equation with Critical Exponent and Robin Boundary

YANG Jing,PU Zhilin,FENG Wei

(1.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan;2.SchoolofMathematicsandInformationsScience,NeijiangNormalCollege,Neijiang641100,Sichuan)

Abstract：In this paper, we study the Kirchhoff equation with nonlinear boundary dissipation and critical exponent of asymptotical state when t tends to infinity, and prove the existence of weak solutions. First, we use the maximal monotone operator theory to prove the local existence and uniqueness of solution, and then we use energy equation to prove the existence of global solution and to give its variation form.

Key words：Robin boundary condition; critical exponent; maximal monotone operators; existence of solution and dissipation; energy equation; variational form

doi:10.3969/j.issn.1001-8395.2016.01.005

中图分类号：O177.92

文献标志码：A

文章编号：1001-8395(2016)01-0026-07

*通信作者简介：蒲志林(1963—),男,教授,主要从事偏微分方程的研究,E-mail:puzhilin908@sina.com

基金项目：四川省科技基础研究项目(2011JY0057)

收稿日期:2014-06-17