广义强非线性拟变分不等式组的迭代算法
佘珺彤, 夏福全
(四川师范大学 数学与软件科学学院, 四川 成都 610066)
广义强非线性拟变分不等式组的迭代算法
佘珺彤,夏福全*
(四川师范大学 数学与软件科学学院, 四川 成都 610066)
摘要:研究一类新的广义强非线性拟变分不等式组解的存在性及算法.首先建立广义强非线性拟变分不等式组与不动点问题的等价关系.利用这一等价关系讨论广义强非线性拟变分不等式组解的存在性与唯一性.然后给出一个含有误差的投影迭代算法.最后证明了该算法产生的迭代序列收敛到广义强非线性拟变分不等式组的唯一解.
关键词:广义强非线性拟变分不等式组; 强单调; Lipschitz条件; 投影动态系统
变分不等式理论,早在20世纪60年代就已经出现[1],并在最优控制、非线性规划、对策理论、物理学、经济与工程学等众多领域有着重要应用.因此许多专家学者对变分不等式问题作了深入的研究,获得了丰富的结果[2-4]等.同时,R. U. Verma[4]首先在变分不等式问题的基础上介绍并研究了变分不等式组并且利用投影算法寻找变分不等式组的近似解.在这之后文献[5-7]对变分不等式组问题作了推广.而拟变分不等式问题出现的时间相对较晚,它在纳什博弈及运输网络平衡等问题上有着广泛的应用,参见文献[8-9]及其参考文献.此外,拟变分不等式问题的结果也可以应用到一些经济与商业模型中[10].但相较于更为成熟的变分不等式问题,拟变分不等式问题在理论分析与算法应用上得到的结果都是有限的,拟变分不等式组的结果就更少了.因而近年来,拟变分不等式以及拟变分不等式组问题引起了越来越多的专家学者的关注和研究.
由于投影动态系统有良好的分析性质,并且其的稳定点集合与变分不等式问题的解集相一致,因此,在近几年,人们考虑应用投影动态系统来分析解决变分不等式问题及其相关问题,获得了丰硕的成果,参见文献[11-15]等.
本文主要利用投影动态系统研究了一类新的广义强非线性拟变分不等式组解的存在性及算法.首先建立了广义强非线性拟变分不等式组与不动点问题的等价关系.通过这一等价关系讨论了广义强非线性拟变分不等式解的存在性与唯一性.然后给出了一个含有误差的投影迭代算法.最后证明了该算法产生的迭代序列收敛到广义强非线性拟变分不等式组的唯一解.
本文假设H为Hilbert空间,它的内积和范数分别记为〈·,·〉和‖·‖.设Ti:H→H,Ai:H→H,hi:H→H和gi:H→H(i=1,2)都是单值映射.Si:H→2H(i=1,2)是一个非空闭凸集值映射.对于给定的常数ρ,η>0.考虑如下问题:
求x*,y*∈H,使得(h1(x*),h2(y*))∈S1(x*)×S2(y*),并且
上述问题称为广义强非线性拟变分不等式组,简称SGQVI.所研究的问题包含以下问题为特例:
当Ai=0(i=1,2)时,SGQVI退化成一类新的广义拟变分不等式组,简记为SQVI:求x*,y*∈H,使得(h1(x*),h2(y*))∈S1(x*)×S2(y*),并且
(2)
当T1=T2=T,h1=h2=h,g1=g2=g,ρ=η时SQVI退化成Q. H. Ansari等在文献[16]中研究的一类变分不等式问题:求x*∈H,使得h(x*)∈S(x*),且
设K是H中的非空闭凸子集,当hi=gi=I(i=1,2),w=v=x,S1(x*)=S2(y*)=K时,SQVI退化成S. S. Chang等在文献[5]中研究的一类变分不等式组问题:求x*,y*∈K,使得
(3)
1预备知识
为了研究广义强非线性拟变分不等式组问题(1)解的存在性和迭代算法以及其算法的收敛性,首先介绍一些有用的定义及定理.
定义 1.1设T:H→H是单值映射,称T是:
(a) 单调映射,如果对∀x,y∈H有
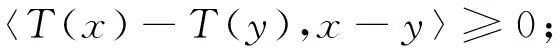
(b)ξ-强单调映射,如果存在一个常数ξ>0使得∀x,y∈H有
(c)μ-Lipschitz连续映射,如果存在一个常数μ>0使得∀x,y∈H有
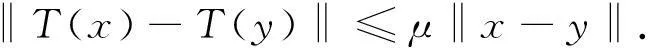
引理 1.1[17]若对任意x∈H,S(x)都是H的一个非空闭凸集,则对一个给定的z∈H,u∈S(x)满足
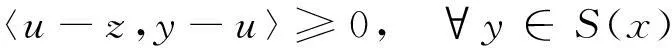
的充分必要条件是u=PS(x)(z),其中PS(x)是H在非空闭凸集S(x)上的投影.进一步,知道投影算子PS(x)(·)是非扩张的,即
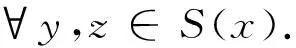
引理 1.2[18]令{an}、{bn}和{cn}是3个非负实数序列,且存在一个自然数n0使得
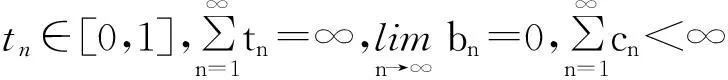
2广义强非线性拟变分不等式组解的存在性与唯一性
定理 2.1设Ti:H→H,Ai:H→H,hi:H→H和gi:H→H(i=1,2)都是单值映射.Si:H→2H(i=1,2)是一个非空闭凸集值映射,ρ,η>0为给定的常数,则x*,y*∈H是广义强非线性拟变分不等式组(1)的解,当且仅当
(4)
证明令x*,y*∈H是广义强非线性拟变分不等式组SGQVI的一个解,使得(h1(x*),h2(y*))∈S1(x*)×S2(y*),并且
由引理1.1,可知(5)式等价于
应用上述引理,证明广义强非线性拟变分不等式组(1)解的唯一存在性.
定理 2.2设Si:H→2H(i=1,2)是2个非空闭凸集值映射.对任意i=1,2,Ti:H→H是ξi-强单调且μi-Lipschitz连续映射,gi:H→H是ζgi-强单调且σgi-Lipschitz连续映射,hi:H→H是ζhi-强单调且σhi-Lipschitz连续映射Ai:H→H是θi-Lipschitz连续映射,并且存在一个常数τ>0,使得
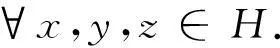
如果存在常数ρ>0,η>0,对所有i=1,2都有
(6)
则广义强非线性拟变分不等式组SGQVI有唯一解.
证明对∀x,y∈H使得h1(x)∈S1(x),h2(y)∈S2(y),定义映射Ψ,Φ:H×H→H如下:
(7)
(8)
在H×H中定义‖·‖*如下:
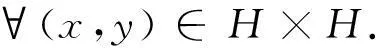
易知(H×H,‖·‖*)是一个Banach空间.
再定义映射F:H×H→H×H如下:
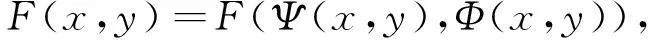
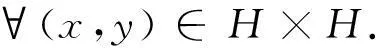
(9)
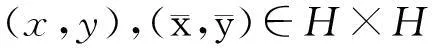

(10)
因为h1是ζh1-强单调且σh1-Lipschitz连续,则有
(11)
因为g1是ζg1-强单调且σg1-Lipschitz连续,则有
(12)
因为T1是ξ1-强单调且μ1-Lipschitz连续,则有
(13)
根据A1是θ1-Lipschitz连续映射可得
(14)
由(10)~(14)式可得
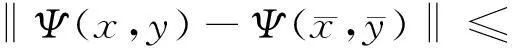
(15)
其中
同理可得
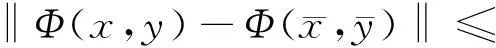
(16)
其中
由(9)、(15)~(16)式可得
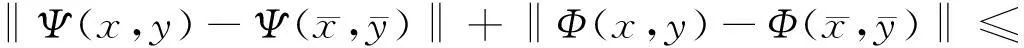
(17)
这里δ=max{κ1+λ2,κ2+λ1}.由条件(6)可得0≤δ<1.并且,由(17)可知F是一个压缩映射.根据Banach不动点定理可知,存在唯一的点(x*,y*)∈H×H,满足(h1(x*),h2(y*))∈S1(x*)×S2(y*),使得F(x*,y*)=(x*,y*).由(7)~(9)式可推出
又由定理3.1.可知x*,y*∈H,使得(h1(x*),h2(y*))∈S1(x*)×S2(y*)是拟变分不等式组(1)的一个解.
注正如M. A. Noor[19]所说,若S(x)=m(x)+K,这里m(x):H→H是一个单值映射,K为H中的非空闭凸子集,则
再设m(x):H→H是γ-Lipschitz连续,易知
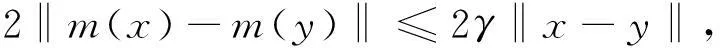
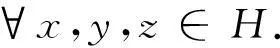
(18)
从而,定理2.2中假设存在一个常数τ>0,使得
∀x,y,z∈H
的条件成立.
3一个新的投影迭代算法及其收敛性
在这一部分,介绍SGQVI的一个含有误差的投影迭代算法,并且证明了这一算法产生的迭代序列最终收敛到广义强非线性拟变分不等式组SGQVI的解.
现将广义强非线性拟变分不等式组的解的配对(x*,y*)所组成的集合记为sol(SGQIV).令Ti,Ai,hi,gi:H→H(i=1,2)都为单值映射,Si:H→2H(i=1,2)为集值映射,ρ>0,η>0为给定常数.若(x*,y*)∈sol(SGQIV),则由定理2.1与定理2.2,可得(h1(x*),h2(y*))∈S1(x*)×S2(y*),且
由(19)式给出下列含有误差的投影迭代算法.
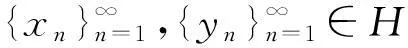
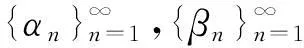
易知,这一含有误差的投影迭代算法包含了一般的投影迭代算法,即如下所述的算法2.
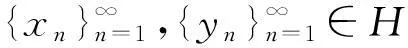
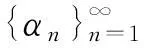
如果Ai=0(i=1,2),则由算法1得到广义拟变分不等式组(2)的含有误差的投影迭代算法.
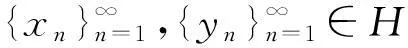
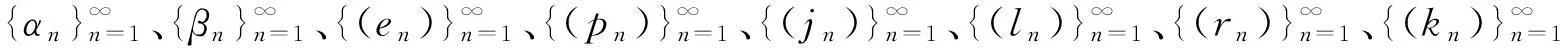
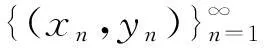
证明由定理2.1和定理2.2可知,广义强非线性拟变分不等式有唯一的解x*,y*∈H.因而sol(SGQIV)是单点集.可以推出
这里序列{αn}与{βn}满足算法1中的假设条件.令
根据算法1中的假设,易知Γ≤0有界.由(20)、(24)式可知
(25)
因为T1:H→H是ξ1-强单调且μ1-Lipschitz连续映射,g1:H→H是ζg1-强单调且σg1-Lipschitz连续映射,h1:H→H是ζh1-强单调且σh1-Lipschitz连续映射,A1:H→H是θ1-Lipschitz连续映射.根据(11)~(14)式相同的证明方法可得
(26)
(27)
(28)
因此,由(26)~(29)式可得
(30)
同理,可得
(31)
这里κi、λi与(15)~(16)式中相同,由(30)~(31)式可得
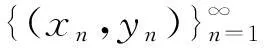
参考文献
[1] STAMPACCHIA G. Formes bilineaires coercivities sur les ensembles convexes[J]. Comptes Rendus de l’Academie des Sciences Serie,1964,258:4413-4416.
[2] BREZIS H. Operateurs Maximaux Monotones et Semigroupes de Contractions dan les Espaces de Hilbert[M]. Amsterdam:North-Holland,1973.
[3] GIANNESSI F, MAUGERI A. Variational Inequalities and Network Equilibrium Problems[M]. New York:Plenum Press,1995.
[4] VERMA R U. General convergence analysis for two-step projection methods and application to variational problems[J]. Appl Math Lett,2005,18:1286-1292.
[5] CHANG S S, LEE H W J, CHAN C K. Generalized system for relaxed cocoercive variational inequalities in Hilbert spaces[J]. Appl Math Lett,2007,20:329-334.
[6] HUANG Z Y, NOOR M A. Generalized system for relaxed cocoercive variational inequalities in Hilbert spaces[J]. Appl Math Comput,2007,190:356-361.
[7] NOOR M A, NOOR K I. Projection algorithms for solving a system of general variational inequalities[J]. Nonlinear Analysis,2009,70:2700-2706.
[8] HARKER P T. Generalized nash games and quasivariational inequalities[J]. Euro J Oper Research,1991,54:81-94.
[9] PANG J S, FUKUSHIMA M. Quasivariational inequality, generalized nash equilibria, and multileader-follower game[J]. Computational Management Science,2005,2:21-56.
[10] YAO J C. The generalized quasi variational inequality problem with applications[J]. J Math Anal Appl,1991,158:139-160.
[11] DONG J, ZHANG D, NAGURNEY A. A projected dynamical systems model of general financial equilibrium with stability analysis[J]. Mathematical and Computer Modelling,1996,24:35-44.
[12] FRIESZ T L, BERNSTEIN D H, STOUGH R. Dynamical systems, variationl inequalities and control theoretical models for predicting time-varying unban network flows[J]. Trans Sci,1993,30:14-31.
[13] NAGURNEY A, ZHANG D. Projected Dynamical Systems and Varaitional Inequalities with Applications[M]. Dordrecht:Kluwer Academic Publishers,1995.
[14] XIA Y S, WANG J. On the stability of globally projected dynamical systems[J]. J Optimization Theory and Applications,2000,106:129-150.
[15] ZHANG D, NAGURNEY A. On the stability of the projected dynamical systems[J]. J Optimization Theory and Applications,1985,85:97-124.
[16] ANSARI Q H, BALOOEE J, YAO J C. Extended general nonlinear quasi-variational inequalities and projection dynamical systems[J]. Taiwanese J Mathematics,2013,17:1321-1352.
[17] POLYAK B T. Introduction to Optimization[M]. New York:Optimization Software,1987.
[18] LIU L S, ISHIKAWA S, MANN W R. Iterative process with errors for nonlinear strongly accretive mappings in Banach spaces[J]. J Math Anal Appl,1995,194:114-125.
[19] NOOR M A. On general quasi-variational inequalities[J]. J King Saud University(Science),2002,24:15-26.
[20] DUPUIS P, NAGURNEY A. Dynamical systems and variational inequalities[J]. Annals of Operations Research,1993,44:19-42.
[21] LIU L S. Ishikawa and Mann iterative process with errors for nonlinear strongly accretivemappings in Banach spaces[J]. J Math Anal Appl,1995,194:114-125.
[22] SIDDIQI A H, ANSARI Q H. An algorithm for a class of quasivariational inequalities[J]. J Math AnalAppl,1990,145:413-418.
[23] SIDDIQI A H, ANSARI Q H. Strongly nonlinear quasivariational inequalities[J]. J Math Anal Appl,1990,149:444-450.
[24] ANSARI Q H, BALOOEE J, YAO J C. Iterative algorithms for systems of extended regularized nonconvex variational inequalities and fixed point problems[J]. Applicable Analysis,2014,93:972-993.
[25] ANSARI Q H, YAO J C. Systems of generalized variational inequalities and their applications[J]. Applicable Analysis,2000,76:203-217.
[26] LIU L J, ANSARI Q H. Systems of quasi-variational relations with applications[J]. Nonlinear Analysis,2010,72:1210-1220.
2010 MSC:47H05; 47J20; 49J40; 90C33
(编辑周俊)
Iterative Algorithms for a System of Extended General Strongly Nonlinear Quasi-Variational Inequalities
SHE Juntong,XIA Fuquan
(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)
Abstract:In this paper, we introduce and study a new system of extended general strongly nonlinear quasi-variational inequalities. First, we establish the equivalences between this system and fixed point problems. By using these equivalences, we discuss the existence and uniqueness of solution to the system. And then, we define a new projection iterative algorithm with mixed errors for finding the unique solution of the system. Finally, we prove the convergence of the suggested iterative algorithm.
Key words:system of quasi-variational inequalities; strongly monotone; Lipschitz conditions; projection dynamical systems
doi:10.3969/j.issn.1001-8395.2016.01.002
中图分类号:O176.3; O178
文献标志码:A
文章编号:1001-8395(2016)01-0008-07
*通信作者简介:夏福全(1973—),男,教授,主要从事优化理论及应用的研究,E-mail:fuquanxia@sina.com
基金项目:教育部科学技术重点项目(212147)
收稿日期:2015-02-06

