多元函数极值的应用分析

赵泽福

(昭通学院, 云南 昭通　657000)



多元函数极值的应用分析

赵泽福

(昭通学院, 云南 昭通657000)

摘要：从方向导数法和梯度、内积法两个方面举例分析了多元函数极值的判定方法。实例研究了多元函数极值在利润最大化、效用最大化以及实际问题等领域中的应用，对于资源的合理配置以及效益的最大化问题提供了技术参考。

关键词：多元函数; 极值; 应用研究

0引言

近年来，随着多元函数极值问题的研究越来越广泛，与多元函数极值相关的分析和研究也越来越深入，使得该方面的理论也相对变得完善，因此，多元函数极值也在诸多领域得到应用，不仅应用于企业单位等利润的计算，同样应用于解决实际生活遇到的问题。文中基于多元函数极值的理论分析，展示了多元函数极值的应用。

1多元函数极值

在多元函数极值的定义中，设二元函数f(x,y)在某点P(a,b)的邻域有定义域，位置P点的自变量增量为ΔP(m,n)，由此可以得到该函数的增量值为Δf=(a+m,b+n)-f(a,b)，如果Δf>0，则P(a,b)为该函数的极大值点，反之则为该函数的极小值点，极大值点所对应的函数值为极大值，反之为极小值，两者统称为多元函数的极值。

方程组

中解为该函数的稳定点。

如果函数在P(a,b)点存在两个偏导数，并且P(a,b)为函数的极值点，则

函数f(x,y)在某点P(a,b)的邻域存在二阶连续偏导数，让

Δ=B2-AC1)如果 Δ<0，则P(a,b)为函数的极值点，当A>0时，P(a,b)为函数的极小值点；当A<0时，P(a,b)为函数的极大值点；

2)如果Δ>0，则P(a,b)不是该函数的极值点。

2多元函数极值的判法

2.1方向导数法判定多元函数的极值

设某函数f(p)在p0点处连续，存在r>0，并且有f(p)在去心邻域中可微，如果Dp0p-f(p)在去心邻域中保持符号不变，则该多元函数在p0处有极值。并且当Dp0p-f(p)为正值的时候，多元函数存在极小值；反之存在极大值。

举例：求解f(x,y)=x2-2xy+3y2-2x+2y+10是否存在极值，如存在，求其极值大小。

解

经计算得x=1，y=0。

由此可知，该函数中(1,0)点的任意方向导数都是0。另

由最后的函数式可以看出，Dp0p-f(p)≥0，因此，可以判定该函数是存在极值的，并且存在极小值，极小值为f(1,0)=9。

2.2梯度、内积法判定多元函数的极值

设定函数f(x)为Rn→R的函数，并且要求x0=(x1,x2，…,xn)∈Rn,B(x0,δ)为x0的邻域，如果函数在该邻域范围内为连续函数，则B0(x0,δ)是可以进行微分的，由此可以推导出：

1)如果(x-x0)·grandf(x)<0,则函数f(x)在x0处存在极大值；

2)如果(x-x0)·grandf(x)>0,则函数f(x)在x0处存在极小值。

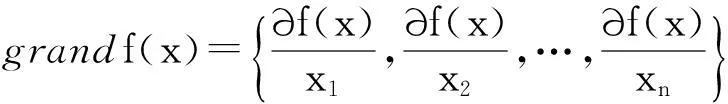
当f(x,y)=g(u(x,y),v(x,y))时，有

举例：判定函数f(x,y)=2x2+10y2-12x+20y-6极值。

解

解得，x=3,y=-1。

判定

所以函数在点(3，-1)处存在极小值f(3,-1)=-34。

3多元函数极值的应用

3.1利润最大化问题的应用

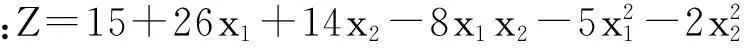
x2----报纸广告费用支出,万元;

Z----企业商品销售的总收入,万元。

根据广告与收益的关系，求最佳的广告方式，使得企业的收益最大化。

解：企业收益值为商品销售值与广告投入费用值的差值，设企业的最大利润值为：

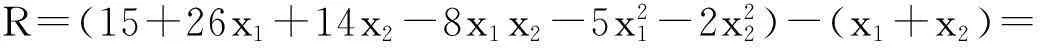
R=(15+26x1+14x2-8x1x2-5x21-2x22)-(x1+x2)=

求解参数的极值，并赋予极值的条件得：

通过极值条件公式可以得到驻点值为x1=1/6万元，x2=35/12万元。

而利润函数在驻点的矩阵为：

由于该函数的驻点矩阵为负矩阵，由此可得利润函数在驻点位置的值为极大值，也就是该企业广告策略的利润最大化，即电视广告费用为1/6万元，报纸广告费用的支出为35/12万元，这样可以获得最大利润点。

企业单位借助于多元函数的极值可以很好地解决利润最大化的问题，通过极值的运用，企业不仅可以在支付和收入之间寻找一个均衡点以获取利润的最大化，还可以在限定一定的预算支出情况下找到费用支出的最佳点，实现资金资源的最佳利用和资源最优配置，这对于企业追求利润最大化来讲，多元函数极值的应用起到了决定性的作用。

3.2效用最大化问题的应用

在经济学中，经常会涉及到效应最大化的问题，在解决该种类型的问题中，通常借助于拉格朗日乘数法来对此类问题进行解答。消费者在进行消费中，所追求的就是效用最大化，即对所购商品的满意度程度的最高化。举例，设定消费者的效用函数为F=f(x1,x2)，进行消费中，预算的边界条件为I=p1x1+p2x2，对此进行拉格朗日乘数法运算，得：

式中:λ----拉格朗日的乘数值。

在拉格朗日乘数方程的基础上设定效用最大化的一阶函数，即：

由第一阶函数的条件可以得到F1/F2=p1/p2，其中F1/F2表示消费者所购商品的边际替代率。因此，消费者效用最大化的条件是：两件商品价格之间的比值等于两件商品的边际替代率，另外拉格朗日的乘数值等于货币的边际效应。由此可以推出，消费者效用最大化的条件是消费者在每一个商品中最后一元钱所获得的效用都是一致的，并且该商品的边际效用与货币的边际效应值相等。

在经济学中，通过对多元函数极值的应用，可以很好地将其运用到商品经济的消费中来，这样消费者可以借助于多元函数的极值问题找到在一定的消费预算和效用的平衡点，帮助消费者选择性价比最佳的商品，达到消费者满意程度的最大化。

3.3解决实际问题的应用

多元函数的极值不仅可以应用于企业最大利润化的运营策略，在实际问题中，还可以解决一些切合实际的问题，例如，某考试中心承办一次考试，借用高校的教室作为考试的考场，该高校的教室有两种，大教室最大容纳考生的数量为50人，每一个教室的租金是70元；小教室最大容纳考生的数量为30人，每一个教室的租金是40元。另外每一个大考场需要配备3名监考老师，小考场配备2名监考老师。在这次考试中，考生数量为1 800名，可以参加考试监考教师的数量为114人，求在满足本次考试的前提下，如何安排考场才能做到租金的最小化。

解：设需要大教室的数量为x1，需要小教室的数量为x2，则租金的最小化数学模型为

Z=min{70x1+40x2}

如果已知条件可以得到函数方程

式中：x1,x2----均为正数。

将最小化租金模型转换成标准型为

Z=min{70x1+40x2+0x3+0x4}

将函数方程转换成：

式中：x1,x2,x3,x4----均为正数。

可以得到全部函数的允许值为：

得

f(Yu1)=70×18+40×30=2460

在对考场布置问题的举例中，借助于多元函数的极值很好地将资源进行了最优配置，实现了资源的最佳利用价值，在实际生活中避免了资源的浪费。除此之外，在实际生活中诸多领域都会运用到多元函数的极值问题，诸如交通运输的最佳道路选择、运筹学中的最佳物流路线等，都会在一定程度上运用多元函数的极值帮助其解决实际问题。由此可见，多元函数的极值在实际生活中起到了良好的助推作用，有效地实现了资源的合理配备。

4结语

介绍了多元函数极值的定义及其性质，了解多元函数极值的判定准则和定理，并在此基础上，推导了两者多元函数极值的判定方法，通过实际举例，很好地将多元函数的判定方法进行了全面的分析和概括，对于以后多元函数极值的判定中，可以灵活地运用不同的判定方法。最后通过实际案例的方式研究了多元函数在各领域的应用，借助于多元函数极值的应用，对于企业利润最大化、消费者效用最大化以及生活实际问题等进行了解决，这对于各行业和各领域都起到了一定的择优选配的作用，有效地实现了资源的合理利用和优化配置。

参考文献：

[1]潘武敏.多元函数条件极值的充分性条件研究[J].科技信息，2007(25)：202-203.

[2]李玲.关于多元函数极值问题的注记[J].重庆职业技术学院学报,2006，15(2)：163-165.

[3]谭琨.多元函数极值的研究与应用[J].安庆师范学院学报:自然科学版,2005,5(2):32-35.

[4]苏兴花.多元函数的极值及其应用[J].科技创新与应用,2012(5):273-274.

[5]北京大学数学系几何与代数教研室代数小组.高等代数[M].北京：高等教育出版社,2003.

Application of multivariate function extreme value

ZHAO Zefu

(Zhaotong University, Zhaotong 657000， China)

Abstract：With the directional derivative method and gradient/inner product methods, the determination of the multivariate function extreme values are analyzed. The applications of multivariate function extremum values in profit maximization and utility maximization are studied, which offer useful technical solutions for the problems of profit maximization and rational resources allocation.

Key words：multivariate function; extreme; applied research.

中图分类号：O 175

文献标志码：A

文章编号：1674-1374(2016)01-0098-04

DOI:10.15923/j.cnki.cn22-1382/t.2016.1.20

作者简介：赵泽福(1974-)，男，汉族，云南镇雄人，昭通学院讲师，主要从事基础数学及微分方程方向研究,E-mail:285307087@qq.com.

基金项目：云南省教育厅科学研究基金(2015Y481)

收稿日期：2015-11-11