K-means初始聚类中心选取优化算法
孙 佳, 胡 明, 赵 佳
(长春工业大学 计算机科学与工程学院, 吉林 长春 130012)
K-means初始聚类中心选取优化算法
孙佳,胡明*,赵佳
(长春工业大学 计算机科学与工程学院, 吉林 长春130012)
摘要:提出了一种利用重心优化初始聚类中心的算法BKM(Barycenter K-Means)。首先将每个候选点临域内所有数据点的重心作为初始聚类中心,然后引入MapReduce进行并行处理计算。结果表明,BKM算法选取的初始聚类中心更为合理,取得了较好的聚类效果。
关键词:聚类; K-means算法; 初始聚类中心; 算法优化
0引言
随着数据时代的到来,数据挖掘技术已经成为当前的研究热点之一[1-4]。聚类分析[5]是数据挖掘领域中一个重要的研究方向,它是将数据集划分成若干个子集,使得每个子集内部的对象相似度较高,而不同子集之间差异性较大。聚类算法大致可分为五类[6]:基于划分的方法、基于层次的方法、基于密度的方法、基于网格的方法和基于模型的方法。其中,K-means算法是基于划分的经典聚类算法之一[7-8],由于其操作简单、收敛速度快等特点,得到了广泛的应用。但是传统的K-means算法也存在着一些不足之处,首先算法对初始的k个聚类中心有较大依赖性,不同的初始聚类中心得到的聚类结果也不一样,使得初始聚类中心的选取成为影响聚类结果的质量的重要因素之一,传统的K-means算法的初始聚类中心是随机选取的,容易陷入局部最优;再者算法对噪音和离群点敏感;另外,从K-means 算法框架可以看出,该算法需要不断地根据计算后的聚类中心进行分类调整,因此当数据量非常大时,算法有较大的时间开销。
目前,很多研究者对K-means算法进行了改进[9-13]。文献[14]提出了一种基于最大最小距离法选取初始聚类中心的方法,算法能够计算出K值,并找出K个合理的聚类中心,但是算法容易选定边缘数据作为初始聚类中心,而且需要较大时间消耗。文献[15]用密度函数法求得样本空间的多个聚类中心,并结合小类合并运算,避免局部最小,但是算法具有较大的时间开销。文献[16]根据聚类对象分布密度函数来确定多个初始聚类中心,但是算法的时间复杂度较高。
针对上述问题,文中提出了一种新的基于初始聚类中心选取的改进算法KMM,通过对候选点μ范围的数据点的重心进行选取,作为初始聚类中心,采用MapReduce并行框架对提出的算法进行实现。实验结果表明,KMM算法能够有效地排除噪声点和孤立点,选取合理的初始聚类中心,从而得到较佳的聚类结果,减少算法迭代次数,并且应用MapReduce并行处理框架,使算法的运行更为高效。
1理论基础
定义1两个数据对象间的欧氏距离
(1)
其中,xi=[xi1,xi2,…,xin],xj=[xj1,xj2,…,xjn]是具有n个属性的两个数据对象。
定义2 簇均值
(2)
定义3 误差平方和准则函数
(3)
式中:Mk----簇Ck中数据对象的中心;
q----簇Ck中的数据对象。
定义4 重心公式
(4)
式中:pi----候选点μ范围的数据点。
2K-means算法基本思想
传统的K-means算法基本思想:首先从数据集中随机选取k个数据作为初始聚类中心,计算数据集中其他的数据对象到k个初始聚类中心的距离,并将其划分到离它最近的聚类中心所在的簇中;然后计算每个簇的均值作为新的聚类中心,不断重复这一过程,直至误差平方准则函数收敛,迭代终止。
传统K-means算法过程如下:
输入:数据集D={x1,x2,…,xn},初始k值,迭代终止条件ε。
输出:满足终止条件的K个簇以及迭代次数n。
1)在数据集D中随机选择k个对象作为初始聚类中心。
2)计算D中剩余对象到每个初始聚类中心的距离,并将其划分到距离最近的聚类中心所在的簇中。
3)重新计算每个簇的均值作为新的聚类中心。
4)计算此时的误差平方和准则函数,若满足|Jc(I)-Jc(I-1)|<ε,其中ε为设定的一个极小参数,算法终止。
5)否则,继续执行步骤2)。
3一种新的K-means聚类中心选取算法
传统的K-means算法的初始聚类中心是随机选择的,然而通过对K-means算法的分析发现,初始聚类中心的选择会对聚类结果造成较大影响。文中提出的算法首先选取某数据点作为候选点,计算该候选点μ范围的数据点的重心作为第1个初始聚类中心,然后选取离该聚类中心最远的点作为第2个候选点,重复计算重心的过程,依次类推,直到选完k个初始聚类中心。这样选取初始聚类中心的优势在于一方面通过对候选点μ范围数据的筛选,能够排除离群点和噪音数据,另一方面将一定范围内的数据的重心作为初始聚类中心,能够降低算法的迭代次数,并且取得较好的聚类效果。
算法描述如下:
输入:数据集D={x1,x2,…,xn},初始k值。
输出:k个初始聚类中心。
(a)设数据集D中有n个对象,D={x1,x2,…,xn},从中任取一个数据点,如xi作为初始候选点,计算xi与其他数据点的距离。
(b)选取与xj距离小于μ的数据点,若存在,计算的范围内所有数据点的重心G1作为第一个聚类中心点,否则,返回步骤(a)。
(c)选取距离G1最远的数据点xj作为第二个候选点,并计算xj与其他剩余数据点的距离。
(d)重复步骤(b),直到选取k个初始聚类中心。
4实验
4.1实验描述
实验是在搭建的hadoop2.0平台上运行的,实验环境中的集群共9个节点,其中,1个master节点和8个slave节点。在集群的众多节点中,每台机器的配置均是相同的(CPU主频3.4 GHz、2.0 G内存、1 T硬盘),为了测试算法的性能,文中选取UCI机器学习数据库中的Iris和KDD Cup 1999 Data Set两个不同规模的数据集作为实验数据进行测试。
将文中提出的算法与原始K-means算法进行以下性能方面的对比分析:
1)聚类结果的准确率方面的对比;
2)算法运行的迭代次数方面的对比;
3)算法的运行时间的对比。
4.2结果及分析
两种算法在Iris数据集上的测试结果见表1。
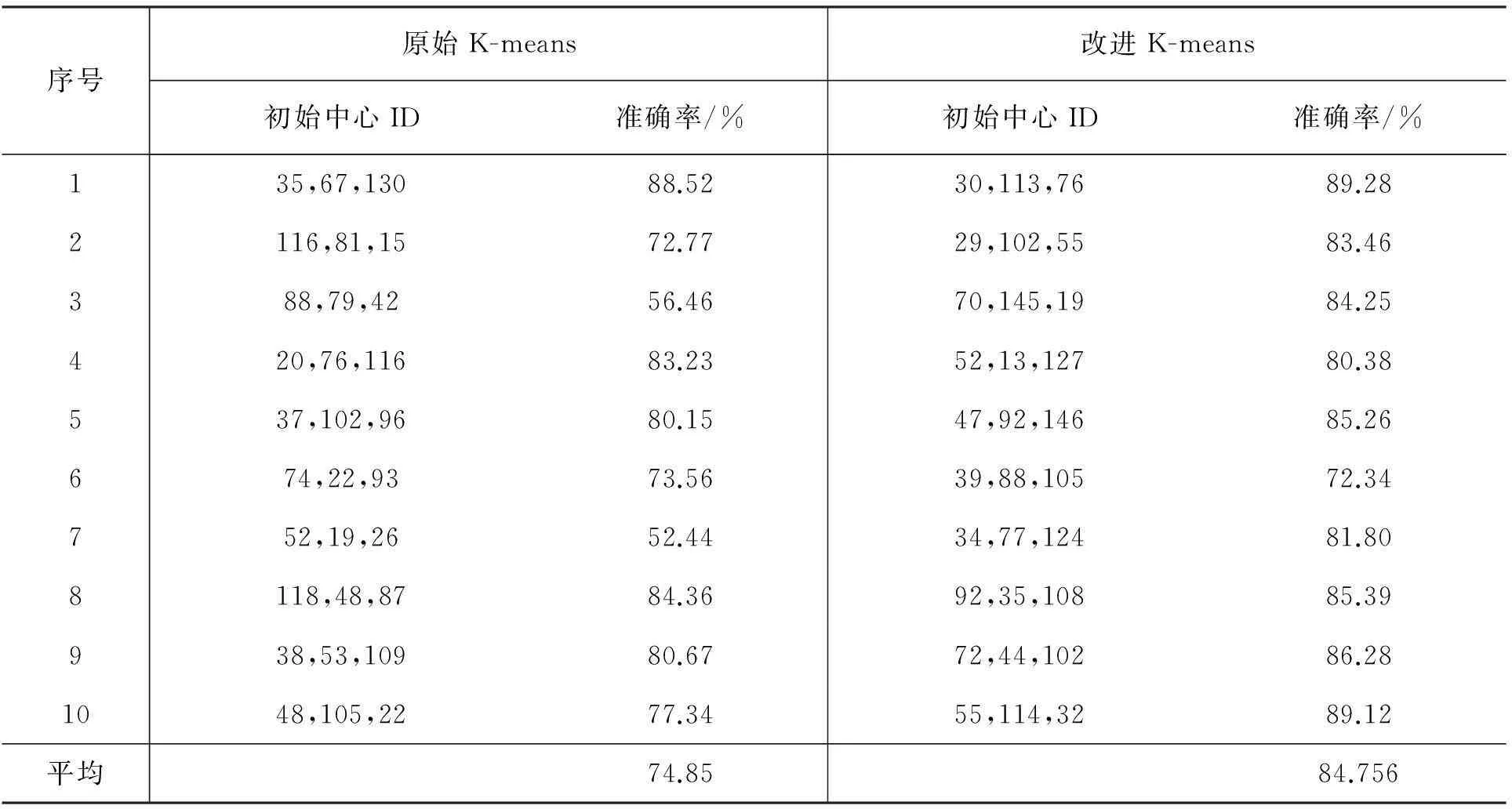
表1 两种算法在Iris数据集的测试结果
表1中可以清楚地看到,原始K-means算法的准确率最高为88.52%,最低为52.44%,平均值为74.85%,准确率的范围波动很大,这也是由于原始K-means算法在选取初始聚类中心点时采用随机选取的方法,并不能保证每次选取的聚类中心都是合理的,当初始聚类中心点选取不当时,就容易导致聚类结果的准确性较低。而文中提出的改进算法准确率最高为89.28%,最低为72.34%,平均值为84.756%。算法在准确率方面总体高于原始K-means算法,说明提出的改进算法选取的初始中心点更为合理,得到的聚类结果更为准确。
将两种算法分别运行10次。Iris数据集有150条数据,每条数据包含4个属性,数据集分为3类。将两种算法在准确率方面进行对比,这里准确率表示为:
式中:c----能够被正确分配到指定类的数据对象的个数;
N----全部数据对象个数。
两种算法在Iris数据集上运行时的迭代次数比较依然是在Iris数据集上进行的测试。如图1所示。
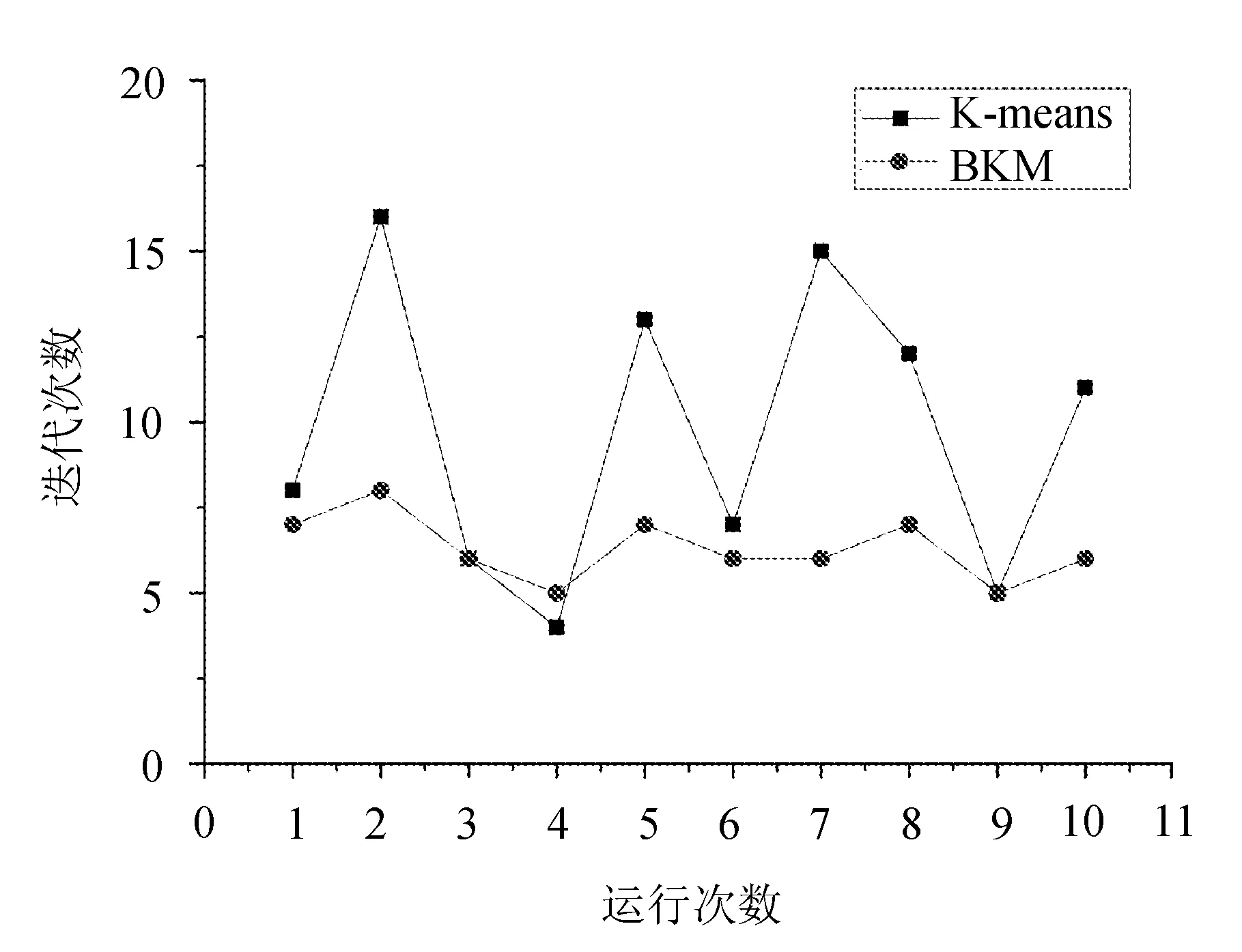
图1 两种算法在Iris数据集上运行时的迭代次数比较
从图1可以看出,选择的初始聚类中心不同,那么算法的迭代次数也不相同,原始K-means算法的迭代次数较为不稳定,波动幅度很大。这种现象说明,如果选取的初始聚类中心离实际各簇中心点较远,会导致目标函数收敛速度慢,造成算法迭代次数的增加。从图1很容易看出,文中提出的改进算法在迭代次数方面明显少于原始K-means算法。说明改进的算法得到了与实际数据的簇中心点较为接近的初始聚类中心点,使得算法收敛速度更快,加快了聚类的过程,得到了较为稳定的聚类结果。
两种算法的运行时间和数据量的关系如图2所示。

图2 算法的运行时间和数据量的关系图
随机选取KDD Cup 1999 Data Set的2 000~10 000条数据进行算法验证。从图2可以看出,我们提出的改进算法在数据量少的时候和原始K-means算法的运行时间相差较少。而随着数据量的不断增加,原始K-means算法的执行时间呈几何增长趋势,说明原始K-means算法对数据集的变化较为敏感,当数据规模增长时,它的执行时间也会大幅度增长,这并不利于大规模数据的处理。相比较而言,文中提出的改进算法的执行时间虽然也呈增长的趋势,但是相对原始K-means算法来说,幅度增长较为缓慢,算法整体的运行时间少于原始K-means算法。这是由于改进的算法应用MapReduce并行处理框架,能够更快速高效地处理大规模数据集。
5结语
研究了基于初始聚类中心的优化算法BKM,将候选点μ范围内的数据点的重心作为初始聚类中心进行聚类。有效地解决了原始算法中对离群点和噪音数据敏感的问题,并且,算法每次都选取距离较远的点作为初始聚类中心,有效解决了算法容易陷入局部最优的缺陷。并将MapReduce并行编程框架引入算法改进中,提高了算法的运行时间。文中所提到的μ,它的取值是一个开放性问题,需要根据具体的数据集的特点进行设定。对于初始K值的选定,将是进一步的研究内容。
参考文献:
[1]Witten, Ian H, Frank, et al. Data Mining:Practical machine learning tools and techniques[J]. Biomedical Engineering Online,2011,51(1):95-97.
[2]Wu X, Zhu X, Wu G Q, et al. Data mining with big data[J]. Knowledge & Data Engineering IEEE Transactions on,2014,26(1):97-107.
[3]Wang S, Shi W. Data mining and knowledge discovery[J]. Springer Handbook of Geographic Information,2011,25(3):545-576.
[4]Yin Y, Kaku I, Tang J, et al. Privacy-preserving data mining[J]. Decision Engineering,2011,2(3):86-92.
[5]朱林,雷景生,毕忠勤,等.一种基于数据流的软子空间聚类算法[J].软件学报,2014,24(11):2610-2627.
[6]孙吉贵,刘杰,赵连宇.聚类算法研究[J].软件学报,2008,19(1):48-61.
[7]陈小全,张继红.基于改进粒子群算法的聚类算法[J].计算机研究与发展,2012,49(z1):287-291.
[8]周炜奔,石跃祥.基于密度的K-means聚类中心选取的优化算法[J].计算机应用研究,2012,29(5):1726-1728.
[9]于海涛,贾美娟,王慧强,等.基于人工鱼群的优化K-means聚类算法[J].计算机科学,2012,39(12):60-64.
[10]Silva A D, Chiky R, Hébrail G. A clustering approach for sampling data streams in sensor networks[J]. Knowledge & Information Systems,2012,32(1):1-23.
[11]毕晓君,宫汝江.一种结合人工蜂群和K-均值的混合聚类算法[J].计算机应用研究,2012,29(6):2040-2042.
[12]Cui X, Zhu P, Yang X, et al. Optimized big data K-means clustering using MapReduce[J]. Journal of Supercomputing,2014,70(3):1249-1259.
[13]王金永,董玉民.改进粒子群算法在数据聚类中的应用[J].长春工业大学学报:自然科学版,2015,36(6):664-672.
[14]Zhang Z P, Wang A J. Easy and efficient algorithm to determine number of clusters[J]. Computer Engineering & Applications,2009,45(15):166-168.
[15]ZHOU Shi bing, XU Zhen yuan. New method for determining optimal number of clusters in K-means clustering algorithm[J]. Computer Engineering & Applications,2010,46(16):1995-1998.
[16]申晓勇,雷英杰,蔡茹,等.一种基于密度函数的直觉模糊聚类初始化方法[J].计算机科学,2009,36(5):197-199.
An optimal algorithm for K-means initial clustering center selection
SUN Jia,HU Ming*,ZHAO Jia
(School of Computer Science & Engineering, Changchun University of Technology, Changchun 130012, China)
Abstract:A Barycenter K-Means (BKM) algorithm with optimized center as initial clustering center is proposed in the paper. At first, the center of all data in the selected region are taken as initial centers and then the parallel MapReduce Processing Framework is introduced into the algorithm. The experimental results show that the selected initial clustering center of the BKM algorithm is reasonable and better clustering results are obtained.
Key words:clustering; K-Means algorithm; initial clustering center; optimized algorithm.
中图分类号:TP 39
文献标志码:A
文章编号:1674-1374(2016)01-0025-05
DOI:10.15923/j.cnki.cn22-1382/t.2016.1.06
作者简介:孙佳(1991-),女,汉族,吉林舒兰人,长春工业大学硕士研究生,主要从事数据挖掘方向研究,E-mail:sunjia_207@126.com. *通讯作者:胡明(1963-),男,汉族,吉林长春人,长春工业大学教授,博士,主要从事分布式计算、数据挖掘方向研究,E-mail:huming@ccut.edu.cn.
基金项目:国家自然科学基金重点项目(61133011)
收稿日期:2015-10-11

