多自由度机器人检测汽车天窗轨迹规划

刘亚梅，　刘　静，　李永盼

(1.长春工业大学 机电工程学院， 吉林 长春　130012;

2.长城汽车股份有限公司技术中心， 河北 保定　071000;

3.河北省汽车工程技术研究中心， 河北 保定　071000)



多自由度机器人检测汽车天窗轨迹规划

刘亚梅1，刘静1，李永盼2,3

(1.长春工业大学 机电工程学院， 吉林 长春130012;

2.长城汽车股份有限公司技术中心， 河北 保定071000;

3.河北省汽车工程技术研究中心， 河北 保定071000)

摘要：以ES165D机器人为载体，以检测汽车天窗的密封性为研究对象，采用改进的遗传算法对机器人各段轨迹进行轨迹规划。利用三维制图软件CATIA建立机器人简易模型，以改进的遗传算法所产生的最优时间间隔为机器人轨迹规划的仿真依据，结合ADAMS进行模型运动学仿真。通过仿真实验对比，得出这种机器人轨迹规划方法不仅能保证最优工作时间，同时能得到机器人平滑的运动轨迹。

关键词：机器人； 轨迹规划； 改进的遗传算法； ADAMS

0引言

近年来，在轨迹规划领域方面，学者们越来越多的将注意点转移到某个优化目标的研究方面，例如，时间优化、能量优化、冲击优化以及各种指标的综合优化等。

文中研究对象为ES165D机器人对汽车天窗密封性的检测，作为汽车外部装饰的汽车天窗，起初应用于高档车型上，现在越来越多地普及到了各个级别的乘用车上[1]。目前,汽车天窗安装点的检测是在每个检测点上安装一个传感器，对每个点进行定位检测。但是怎样使机械手快速完成检测，减少工作时间，提高工作效率，是目前急需解决的一个问题。这就要对机械手运动进行时间最优轨迹规划。

机器人时间最优轨迹是工业机器人研究方向上的重要研究课题之一，它的主要研究内容是在满足机器人运动学和动力学等各种约束条件下以时间为优化目标对机器人进行轨迹优化。实际生产中，出现了很多机器人时间最优化的方法:复合形法、混沌算法、加权系数法等，文中以时间最短为优化目标，采用遗传算法，同时对遗传算法做了详细的分析，主要从SGA(简单遗传算法)、RAGA(改进排序自适应遗传算法)、IAGA (自适应遗传算法)三方面做了分析对比以及仿真实验，并得出结论，遗传算法比其他的优化算法优化性能略好，优化效果明显[2]。所以，文中选用遗传算法优化轨迹，并且将其改进，使其能够更好地进行优化。

1最优时间轨迹规划

1.1时间最短的轨迹优化问题的描述

以笛卡尔空间机器人运动为例，来描述一下时间最短轨迹优化问题。在规定的轨迹内，机器人要经过n个路径点才能完成生产作业任务。通过机器人在笛卡尔空间中的逆运动学运算将经过的n个路径点转换为关节空间的每个关节对应的n个关节角值，将产生的n-1个时间间隔长度记为Ti=(i=1,2,…,n-1)，Ti=ti-1-ti，其中，ti为机器人运动到第i个插值点处的时间[3]。则总运动时间为：

(1)

式中：T----目标函数；

Ti(i=1,2,…，n-1)----设计变量。

机器人在满足各关节轨迹所允许的关节大小、速度、加速度的范围内，以时间最短的问题，可描述为：

(2)

1.2最优时间轨迹规划的遗传算法

1.2.1遗传算法解决问题的流程

遗传算法大致遵循以下3个操作：选择、交叉和变异。

1)选择。选择操作是用来挑选交叉重组对象的，根据适应度计算通过适合的选择方法确定父代操作个体和其产生的子代个体数。

2)交叉。新个体的产生是通过交叉重组获得，但这里得到的新个体基因是继承父代基因信息的。在交叉操作中，有一个重要的算子，即交叉概率，交叉概率是在种群中交叉的个体数与种群大小的比例。

3)变异。变异也可以产生新个体，部分信息遗传父代得到，部分信息是根据外界因数的影响突变获得，它决定后代新环境的适应能力。同样，在变异操作中，也有一个很重要的算子，变异概率即在种群中变异的个体与种群大小的比例。

描述遗传算法须解决六大问题：编码方式选择、种群初始化、适应度函数设计、遗传算子选择、控制参数设置和终止条件设定。

遗传算法解决问题的流程，首先把实际求解最优问题抽象出数学模型，对实际问题进行数学表达，选取问题变量，对变量参数用某种编码方式进行编码，随机选取一定数量编码个体组成初始种群，规定种群规模[4]。然后进行适应度值计算，并进行大小顺序排列，按规定的交叉变异概率进行遗传操作得到新的下一代，检验是否满足算法终止条件，满足得到最优解，解码转化成实际问题的表现型值，不符合再组成新种群返回，再进行适应度评估，直到寻找符合终止条件的最优解为止[5]。

1.2.2改进的遗传算法

根据简单遗传算法的分析，编码方式、控制参数以及运算流程对寻求问题最优解影响巨大，基于文中对时间最优轨迹规划问题描述对遗传算法作相应改进，改善简单遗传算法的不足之处。改进的遗传算法主要从编码方式、遗传算子和流程3个方面进行改进。

1.2.2.1改进编码方式

文中采用的编码方式为实数编码，是以时间间隔作为参变量，所以可以直接利用实数来检验参变量是否满足条件，有利于出路约束条件。传统的二进制编码要求适应度值必须为正数，才能结合约束条件与目标函数进行适应度值计算。实数编码不仅可以减少计算机运算之间的转换，还可以直接反映真实值，给人很直观的结果。

1.2.2.2改进适应度值

1)挑选交叉和变异算子。

交叉概率或变异概率分别影响着交叉或变异方式，所以在选择时必须有度。交叉概率过大，会破坏适应度大的个体的结构；交叉概率过小,会导致过早收敛。变异概率过大，会使种群整体结构发生变化；过小，不容易产生新基因个体。一般情况下，算法的收缩性在交叉概率与变异概率的影响下是固定不变的，所以寻找这两个概率的最优值对适应度值的改进是非常重要的。在自适应遗传算法的应用后，交叉概率和变异概率在算法运行时可以自适应改变，使得算法的性能和收敛速度大大地改善。

假设fmin为种群中最小适应度值，f为变异个体适应度值，f′为交叉后较小适应度值，根据算法描述进行变换：

(3)

(4)

式中：Pc1=0.9，Pc2=0.4，Pm1=0.1，Pm2=0.01。

算术交叉算子为

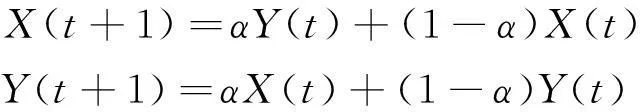
(5)

高斯变异算子为

(6)

2)挑选选择算子。

其次，完善科技人才综合服务平台建设，整合人才引进、人才认定、人才激励配套待遇落实、创新创业扶持等政策和其他生活服务信息，为科技人才提供一站式、全流程、专业化的综合服务。

选择算子采用精英保留策略来搭配，即子代性能较差的个体将被父代中最优良个体直接替代，从而扩大种群规模，增大搜索空间，克服了传统的选择过早和局部收敛缺点，减小了随机破坏优良个体结构的概率问题。生成新的种群不仅含有父代优良个体，又有子代优良个体，还增加了寻求最优解的最大可能性，提高了算法效率。

1.3改进遗传算法的流程

1)确定算法参数：Pc1、Pc2、Pm1、Pm2、N(种群规模)、g(迭代代数)和n(每个关节轨迹时间段数)。

2)约束条件。问题描述中以运动学参数最大值、力矩最大值以及运行总时间不大于15s作为文中优化问题的约束条件。

3)随机生成符合问题描述约束的参变量时间间隔组成初始种群。

4)通过初始种群计算目标函数值，对上述初始种群进行遗传操作生成新种群。

5)扩大种群。将父代种群和子代种群组合，利用精英保留策略结合目标函数值排序，根据约束条件剔除组合新种群(N)。

6)判断是否满足终止条件，即是否满足时间最优为判断条件。如果满足，则终止算法；若不满足，则继续。改进遗传算法来解决文中优化问题的完整流程如图1所示。

图1　改进的遗传算法流程图

2改进遗传算法文中应用

2.1机器人模型的建立及仿真

前期过程中，利用CATIA建立了三维模型并将其导入到ADAMS三维仿真软件中对机器人运动进行运动学仿真，设置仿真时间15s，步长100，机器人模型如图2所示。

仿真结果如图3所示。

以上3种曲线都是光滑的曲线，在每个过渡点处都平稳的过渡。由此可以看出，在模拟仿真过程中，机器人各关节角位移曲线连续平稳，关节角速度及关节角加速度也连续平滑且无突变。这说明模拟仿真实验是成功的，机器人作业时不会产生突变现象，运行过程平稳无冲击。汽车天窗密封性能够进行检测，保证了机器人的正常作业。

图2　机器人模型

图3　关节6运动学参数曲线

2.2优化结果

依据目标函数与改进的遗传算法流程在MATLAB中编制程序，程序采用实数编码方式，各遗传算子和约束条件分别建立相应的.m文件，在模仿生物进化的迭代运算过程中调用这些.m文件即可实现优化。设置优化设置参数：Pc1=0.9，Pc2=0.4，Pm1=0.1，Pm2=0.01，N=50，g=200。对初始值进行10次优化结果见表1。

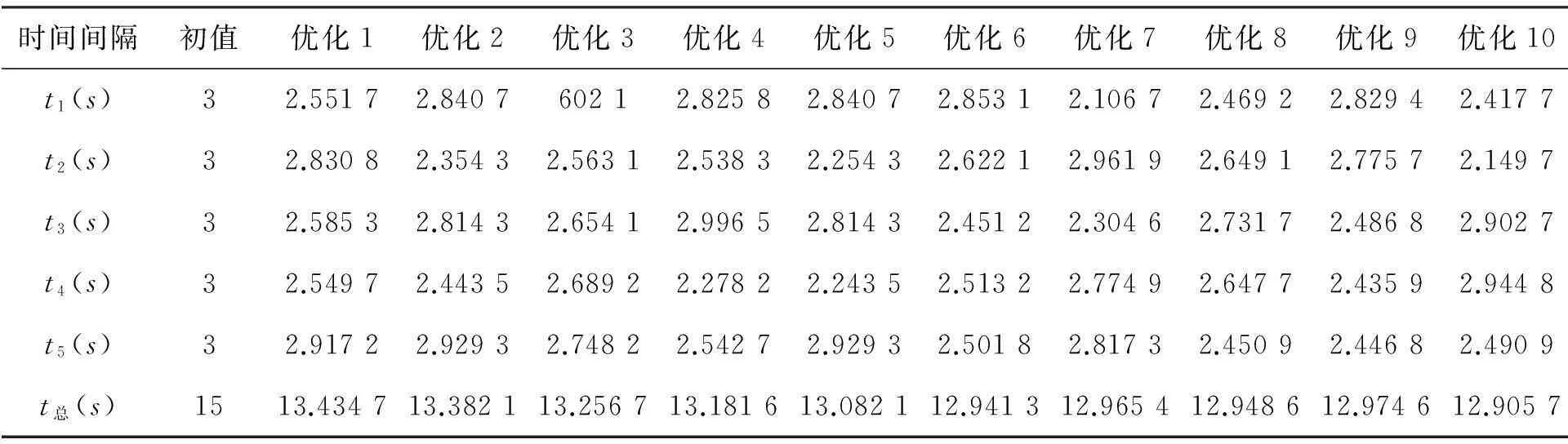
表1　优化后的时间结果

末端执行器优化后的仿真曲线如图4所示。

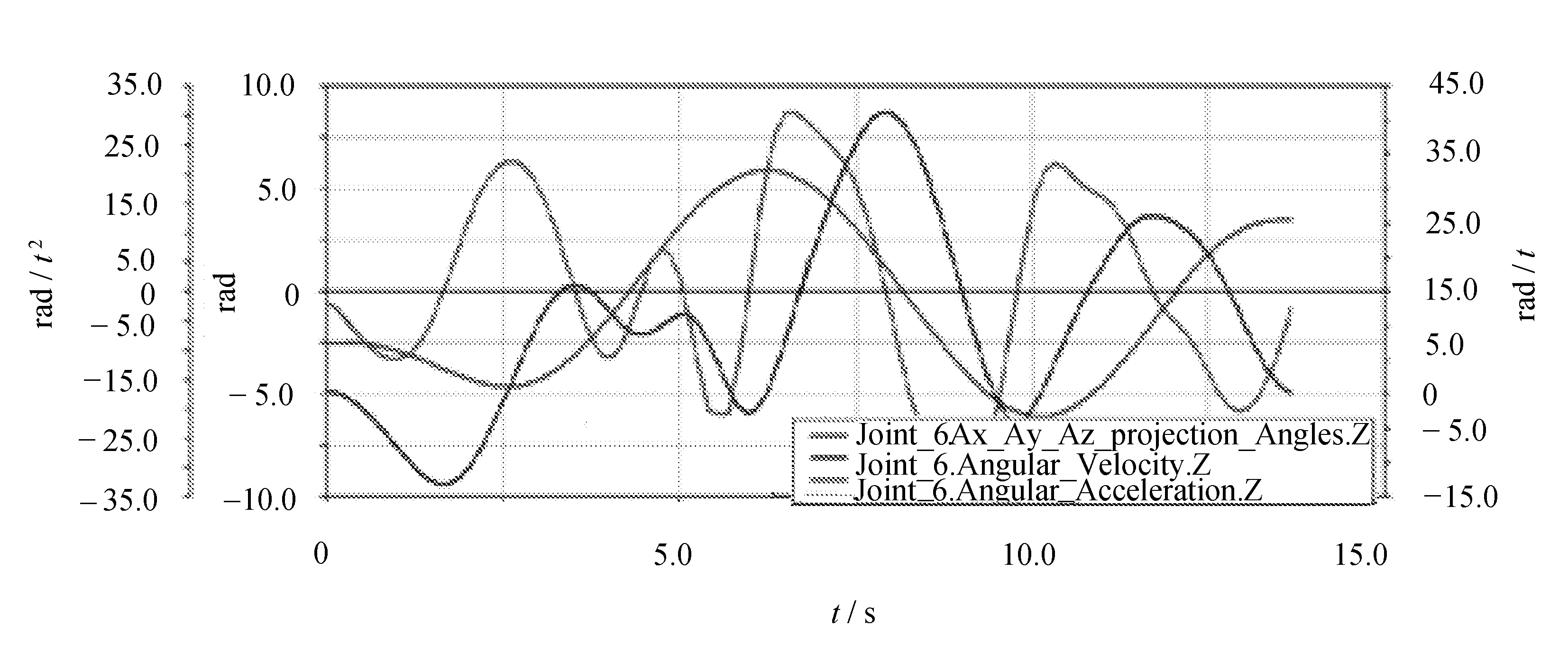
图4　优化后关节6运动学参数曲线

从仿真结果还可以看出，经过遗传算法优化后，机器人运行时间由原来的15.000 0 s减少到了12.905 7 s，比原先减少了2.094 3 s，更重要的是时间的缩短在机器人作业的约束条件之内，在满足机器人运动的前提下提高了机器人工作效率。改进遗传算法轨迹方法对于文中机器人进行汽车天窗密封性的检测基于时间最优的规划非常有效，也达到了文中对最优化问题的解决效果。

3结语

以时间最优作为目标函数，并以此为性能指标，在满足各种约束条件下进行机器人时间最优轨迹规划。通过ADAMS进行机器人仿真，结合遗传算法对各段轨迹进行时间优化，并将优化前后结果进行对比验证。通过对比可以看出，改进后的遗传算法优化方法减少了机器人检测汽车天窗密封性的工作时间，提高了效率，在实际生产中具有一定的指导意义[6]。

参考文献：

[1]李祎鋆.汽车天窗玻璃密封条开启、关闭异响问题的研究[J].汽车使用技术，2012(7):64-66.

[2]张红强.工业机器人时间最优轨迹规划[D].长沙：湖南大学，2004.

[3]牛永康.六自由度串联机器人轨迹规划时间最优研究[D].长春：长春工业大学,2012.

[4]付佳.基于QOS的网络编码资源优化组播路由算法研究[D].北京:北京邮电大学,2011.

[5]李东洁,邱江艳.一种机器人轨迹规划的优化算法[J].电机与控制学报，2009,13(1)：123-128.

[6]王威，徐兵，岳晓峰.基于机器加工时间最短的混合遗传算法[J].长春工业大学学报：自然科学版，2012，33(3)：283-288.

Trajectory planning of a multi-degrees of freedom robot for car skylight test

LIU Yamei1,LIU Jing1,LI Yongpan2，3

(1.School of Mechatronic Engineering, Changchun University of Technology, Changchun 130012， China;2.Technical Center of Great Wall Motor Co., Ltd., Baoding 071000, China;3.Automotive Engineering Technology Research Center, Baoding 071000, China)

Abstract：ES165D robot is applied to test the sealing property of car skylight, and an improved genetic algorithm is used to plan the trajectory of the robot in every motion section. We utilize CATIA to establish a simple robot model and obtain the optimal intervalwith the algorithm to simulate trajectory planning and the mechanism dynamics of the robot in ADAMS. Simulation results show that optimal working time and smooth motion trajectory of the robot can be realized with the algorithm.

Key words：robot; trajectory planning; improved genetic algorithm; ADAMS.

中图分类号：TP 391

文献标志码：A

文章编号：1674-1374(2016)01-0090-05

DOI:10.15923/j.cnki.cn22-1382/t.2016.1.18

作者简介：刘亚梅(1970-)，女，汉族，吉林长春人，长春工业大学副教授，主要从事机械电子工程方向研究,E-mail:liuyamei@ccut.edu.cn.

收稿日期：2015-09-21