求解绝对值方程的光滑化同伦方法

刘子立，　王秀玉

(长春工业大学 基础科学学院， 吉林 长春　130012)



求解绝对值方程的光滑化同伦方法

刘子立，王秀玉*

(长春工业大学 基础科学学院， 吉林 长春130012)

摘要：先构造绝对值函数光滑化函数,利用此光滑化函数对绝对值方程Ax-|x|=b建立同伦方程，用逆像定理证明同伦路径的存在性，用一维流形分类定理证明了同伦路径的收敛性,得到该光滑同伦路径的极限点就是绝对值方程的解。

关键词：绝对值方程; 同伦方法; 同伦路径

0引言

绝对值方程Ax-|x|=b,其中,A∈Rn×n,x∈Rn,b∈Rn是非线性方程组的一种推广,其来源于线性互补问题。首先由Rohn J[1]提出绝对值方程，随后，由学者Mangasarian O L[2]指出求解绝对值方程是NP-hard的。Caccetta L[3]利用磨光技术将|x|磨光，把绝对值方程转化为光滑化问题来解决。

在实际计算中，转化绝对值方程、改进算法、弱化条件是一类重要问题。文献[4-6]详细地介绍用同伦方法求解互补问题，但是，用组合同伦方法直接求解绝对值方程的文献未见发表。文中基于这一点，构造绝对值函数光滑化函数，利用光滑化函数建立同伦方程，证明同伦路径的一些性质，最后得到绝对值方程的准确解。

1预备知识

引理1[7]同伦算法的基本原理。

1)求方程组F(x)=0的解，其中F(x)满足条件：

2)选择很容易求解的方程组:

G(x)=0

其中G(x)满足条件：

3)构造同伦方程组:

观察3)中所构造的同伦方程组，同伦参数t的取值范围是[0,1]，当t=0时，同伦方程组所得到的解就是2)中方程组的解，当t=1时，同伦方程组所得到的解就是要求得的1)中方程组的解。

引理2[8](逆像定理)设φ是U⊂Rn→Rp的一个Cα(α>max{0,m-k})映射，如果0是φ的一个正则值，那么φ-1(0)由一些n-p维Cα流形组成。

引理3[8](一维流形分类定理)一维带边光滑流形的每个连通分支，或者微分同胚于单位圆周，或者微分同胚于区间(0,1]或(0,1)或[0,1]。

定义1[9]设f:D⊂Rm→Rn是光滑映射，且n≤m，则对任意y∈Rn，记f-1(y)为在映射下的逆象，即f-1(y)={x∈D|f(x)=y}。对D中的某一点x0，如果f在x0处的Jacobi矩阵行满秩，则称是映射f的正则值(注:不符合正则值点定义的点称为临界点)。

2主要结果

条件1:

A-(1-t)D可逆。

证:必要性:

若[A-E,A+E]正则，由于A-(1-t)D∈[A-E,A+E]，因此A-(1-t)D可逆。

充分性:

记

i≠j

当bii∈[aii-1,aii]时，∃t∈[0,1],使得

di=1

当bii∈[aii,aii+1]时，

di=-1

因此，总有bii=aii-(1-t)di，从而有B=A-(1-t)D可逆。

即条件1成立，证毕。

构造同伦方程如下:

(1)

当t=1时，同伦方程(1)有唯一解

当t=0时，同伦方程(1)即为绝对值方程。

对给定的x(0)，同伦方程(1)也记为Hx(0)(x,t)，并记

引理6若条件1成立且H由式(1)定义，则Γx(0)是一条有界曲线。

证明:Γx(0)的存在性已由引理6获得。反证，假设Γx(0)无界，则必存在点列

使得

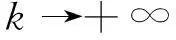
因tk∈[0,1]，{tk}必存在收敛子列，仍记为{tk}，记

由式(1)可得:

(2)

(3)

记

式(3)两边取极限得:

(4)

由式(4)及A可逆，‖(x(*)‖=1，知t*≠1。

记

D=diag(di)

由式(4)得

(5)

由条件1及式(5)得x(*)=0，此与‖x(*)‖=1相矛盾，所以Γx(0)有界。

证明:由引理5、6知Γx(0)是有界曲线,由一维流形分类定理知Γx(0),或者微分同胚于单位圆周、或者微分同胚于单位区间。

由

其中

可逆。知Γx(0)微分同胚于单位区间,记(x(*),t*)为Γx(0)的极限点，只能下列3种情况出现:

1)t*=1,x(*)∈Rn。

2)t*∈(0,1),x(*)∈∂Rn。

3)t*=0,x(*)∈Rn。

H(x(0),x(0),1)=0有唯一解，情况1)不可能出现，由引理6知2)不可能出现，因此只能是3)成立。由此证明了Γx(0)的收敛性，由同伦方程组(1)知Γx(0)极限点为绝对值方程的解。

参考文献：

[1]Rohn J. Atheorem of the alternatives for the equatinAx+B|x|=b[J]. Linear Mnltilinear Algetra,2004,52:421-426.

[2]MangasarianOL,MeyerRR.Absolutevalueequation[J].LinearAlgetraAppl.,2006,419:359-367.

[3]CaccettaL,QuB,ZhouGL.Agloballyandquadraticallyconvergentmethodforabslutevalueequations[J].ComputeOptimAppl.,2009,48:45-58.

[4]王秀玉，姜兴武，刘庆怀.求解互补问题的新同伦算法[J].吉林大学学报:理学版，2012，50(3)：494-499.

[5]姜兴武，王秀玉.P0线性互补问题的新同伦方法[J].吉林大学学报：理学版，2013,51(5)：807-810.

[6]杨泰山，姜兴武，王秀玉.线性互补问题解的存在性[J].吉林大学学报：理学版，2013,51(6)：1063-1067.

[7]田金燕.两种改进的同伦分析方法[D].哈尔滨：哈尔滨理工大学应用科学学院，2014.

[8]李海洋.基于改进的同伦法求解非线性方程[D].鞍山：辽宁科技大学理学院，2013.

[9]赵雅玲，申海明，王秀玉.法锥条件下非凸非线性优化问题的同伦算法[J].长春工业大学学报：自然科学版，2010，31(6)：613-616.

A smoothing homotopy method for the absolute value equation

LIU Zili,WANG Xiuyu*

(School of Basic Sciences, Changchun University of Technology, Changchun 130012， China)

Abstract：First we construct a smoothing function for absolute function. With the smoothing function, we propose a homotopy formula for the absolute equation Ax-|x|=b. The inverse theorem is used to prove the existence of the homotopy path and one-dimensional manifold theorem the convergence. We can come to the conclusion that the limit point of the smooth homotopy path is the solution of the absolute equation.

Key words：absolute value equation; homotopy algorithm; homotopy path.

中图分类号：O 221

文献标志码：A

文章编号：1674-1374(2016)01-0095-03

DOI:10.15923/j.cnki.cn22-1382/t.2016.1.19

作者简介：刘子立(1989-)，男，汉族，内蒙古兴安盟阿尔山人，长春工业大学硕士研究生，主要从事最优化理论与算法方向研究,E-mail:1271372108@qq.com. *通讯作者：王秀玉(1965-)，女，汉族，吉林长春人，长春工业大学教授，硕士，主要从事最优化理论与算法方向研究,E-mail:1062775175@qq.com.

基金项目：吉林省自然科学基金资助项目(201215128)

收稿日期：2015-10-08