6R机器人运动学分析及奇异处理研究

柳　贺，刘　蕾，曾　辉，李　勋，万　君

(安徽埃夫特智能装备有限公司 蔡鹤皋院士工作站，安徽 芜湖　241009)



6R机器人运动学分析及奇异处理研究

柳贺，刘蕾，曾辉，李勋，万君

(安徽埃夫特智能装备有限公司 蔡鹤皋院士工作站，安徽 芜湖241009)

摘要：针对机器人逆运动学过程中存在运算复杂、多组解的选取问题，提出了一种6R机器人逆运动学的几何方法.在求解的推导过程中，采用几何法与双变量正切函数相结合避免了失解，针对有多组逆解的情况，采用“插补连续性”的最短路径与最优标志设置准则相结合选取一组最优解，同时考虑奇异位的避让，满足实际工程中的需要，在公司生产的多款机器人中获得了成熟应用.

关键词：工业机器人；逆运动学；奇异；插补连续

机器人运动学分析，包括正逆运动学分析，正运动学为由机器人各关节角度来确定机器人的TCP位姿，而逆运动学根据工具坐标系相对于基坐标系的目标位姿，求解机器人各关节角[1].逆运动学在机器人学中占有非常重要的地位，是机器人轨迹规划和运动控制的基础，直接影响着控制的快速性与准确性.一般机器人运动学逆解算法可分为以下几种：解析法[2，3]( 又称反变换法)和数值解法，其中反变换法求解过程直观，因而被广泛采纳，但其求解过程中需多次进行矩阵变换的逆运算和4*4维矩阵的乘积运算，导致求解过程复杂耗时[4].

目前大多数6R工业机器人的几何结构都满足Pieper准则，即3个相邻关节轴线交于一点或相互平行，其运动学逆解可以得到数量一定的若干组封闭解，一般为8组或16组，对于后3个关节为旋转关节而且轴线相交于一点的6R工业机器人，其前3个关节决定末端执行器的位置，后3个关节决定末端执行器的姿态[5-7].

图1　机器人坐标系的建立Fig.1　robot coordinate system

本文以自己公司生产的ER165C机器人为研究对象，提出基于几何法的运动学分析方法，计算量小，便于实时控制，同时对多解进行有效选取，并对奇异位置进行分析与避让处理.

1建立坐标系

一般方式的建立坐标系方法，如图1所示，建立相应的各个关节的坐标系，规定与轴满足右手法则(右手系)转角为正方向.其中全局坐标系为O0- X0 Y0 Z0，简记为O系.各个关节为1，2，3，4，5，6系，工具坐标系为T系.在初始位姿下与T系重合的全局坐标系为GT系.

2机器人运动学正解

已知各个关节的转角，求得机器人工具端OT的姿态和位置，即为机器人的正解.用坐标变换来描述为从O到T的变换[8].从图1可知，从0到1的变换矩阵为1T0.依次类推2T1、3T2、4T3、5T4和6T5.从而可以得到从0到6的坐标变换6T0.从0到T的变换为TT0=6T0TT6.

其中：z0=710;x1=400,x2=1100,x3=225,y3=1110,zT=280用齐次坐标变换矩阵来表示机器人的正解运算如下式(1)所示：

TT0=1T02T13T24T35T46T5TTT6

(1)

3机器人运动学逆解

已知末端的位姿，求得各个关节的转角就是机器人的逆运动学求解.采用几何法进行求解，过程如下：

通过T系和变换TT6，可以求得腕部关节处6T0的变换矩阵.6T0=TT0(TT6)-1.利用这个关系可以进行逆解求解[9].

3.1第一关节角θ1求解

参见图2，从几何关系中可以看到腰部旋转角度求解为两解，分别为前腰(Front)与后腰(Back)：

θ1=arctan2(yp,xp)

(2)

(3)

3.2第二关节角θ2求解

考虑θ1解的情况，参见图3，则有：

图2　第一关节角θ1计算　　　　　　　　　　　　图3　第二关节角θ2计算Fig.2　solution of joint 1　　　　　　　　　　　　Fig.3　solution of joint 2

从图3可以看出：

(4)

另一个角度θb为：

θb=arctan2(2yp,2xp)，

(5)

于是第二个关节角θ2为：

θ2=θb-θa

(6)

显然这个值有两个解，另一个解见图4，分别为高臂(Convex)与低臂(Concave).

3.3第三个关节角θ3求解

见图5，先求初始角度：

从而得到角度：

θ3=-(θd-θc)

(7)

另一个解θ3为：

(8)

图4　第二、三关节角的另解　　　　　　　　　　　图5　第三关节角计算Fig.4　another solution of joint 2 and 3　　　　　　　　Fig.5　solution of joint 3

3.4第四、五和六个关节角θ4、θ5、θ6求解

关于旋转的解，则按式:

6T0=1T02T13T24T35T46T5和6T3=2T31T20T16T0=4T35T46T5

于是有：θ5=±arccos(6T3(3,3))的两个解，为高手腕(Positive)与低手腕(Negative ).

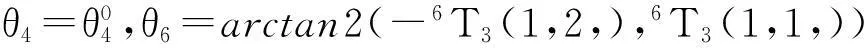
3.5机器人的多解选取

逆解存在多解，而机器人的运动控制需要唯一的确切解.首先，若关节角关节运动范围超过上述的值域范围，则在必要情况下，需将求得的关节角可能解加减360度，补出关节运动范围内的其他可能解，特别在第四与第六关节[10]；其次，选取关节运动范围内的可能解；最后，由运动插补连续性，选取与该关节角上一插补周期的值距离最近的可能解为唯一最优解.各关节角的求解顺序为[11]：先确定的唯一最优解，再利用θ1的解按照上述方法和多解处理步骤求取其余关节角的解.最后所得的这组唯一的最优关节角即可作为实现机器人目标位姿的关节控制输入[12-13].

但在实际应用中，往往需要直接调用机器人的运动学库，这时无法按照插补的连续性进行选解，需要对运动学确定选解最优设置：比如FIAG=Front+Convex+Positive等模式进行选解.

4机器人奇异解的判断与避让处理

若目标P点的yP=0且xP=0时，θ1自由度丢失，其变化不影响腕部的位置，此时θ1为无穷多组解，该种情况在机器人空间内出现的机会比较少，一般做θ1取上个插补周期的值.

若6T3(3,3)=1，也就是θ5=0，关节4和6的旋转轴线共线，此时θ4+θ6有唯一解，而θ4与θ6有无穷多种组合，实际工程中一般进行在θ5接近0度时，进行报警停止与奇异位提示，或者进行自动转换到关节空间，θ5过零后回到插补空间，但这样会损失部分线性精度.

5ER165C机器人的运动控制验证

按照上述的算法封装成运动学库，分为：TRF_FOR正解与TRF_INV逆解，在每个插补周期，路径规划控制器调用运动库函数进行轴运动控制.

采用实际工程中的控制器离线仿真软件进行实际轨迹控制，轨迹为一圆弧，圆弧上四点的位姿为：

cp0:CARTPOS:=(x:=1880.77,y:=218.5,z:=1460.3,a:=0,b:=59.3865,c:=180,mode:=0)

cp1:CARTPOS:=(x:=1880.77,y:=-181.5,z:=1060.3,a:=0,b:=59.3865,c:=-180,mode:=0)

cp2:CARTPOS:=(x:=1880.77,y:=-581.5,z:=1460.3,a:=0,b:=80.53,c:=-172.5,mode:=0)

cp3:CARTPOS:=(x:=1880.77,y:=-181.5,z:=1860.3,a:=0,b:=51.68,c:=-180,mode:=0)

测试TCP与各轴位移如下图所示：

图6　3D实际运行监视　　　　　　　　图7　各关节运动位移图　　　　　　　　　　图8　TCP的位姿图　　　Fig.6　3D model view　　　　　　　　　Fig.7　positions of 6 joints　　　　　　　　　　Fig.8　positions of TCP

由图7(纵轴从上至下为θ1-θ6的值，单位：° ；横轴为时间轴，单位：s)与图8(纵轴从上至下为TCP的X、Y、Z、A、B、C的值，单位：mm与°；横轴为时间轴，单位：s )可以看出，机器人在复杂的圆弧运动中，其位姿均大幅运动，能够平稳的实现圆弧插补运动，表明了该六自由度机器人的运动学算法完善，可以达到期望的目标.

6结论

在机器人逆解求关节角度过程中，采用几何法进行逆解运算，比一般的解析算法更加简单高效，便于实时控制；本文给出了六自由度机器人对应某一位姿的多组解，采用“插补连续性”的最短路径与最优标志设置准则相结合选取一组最优解，满足实际工程中的需要.

参考文献：

[1]刘鹏,宋涛,鵭超,等.焊接机器人运动学分析及轨迹规划研究[J].机电工程,2013,(4):390-394.

[2]SAEED B， NIKU. Introduction to Robotics[M]. BEIJING: Publishing House of Electronics Industry,2013.54-57.

[3]扶宇阳,葛阿萍.基于MATLAB的工业机器人运动学仿真研究[J].机械工程与自动化,2013,(3):40-42.

[4]Hudyjaya SiswoyoJo, Nazim MirNasiri. Dynamic modeling and walk simulation for a new four-degree of-freedom parallelogram bipedal robot with sideways stability control[J]. Mathematical and Computer Modelling, 2013,(1):25-28.

[5]苏学满,孙丽丽,杨明,等.基于Matlab的六自由度机器人运动特性分析[J].机械设计与制造,2013,(1):78-80.

[6]谢斌,蔡自兴.基于MATLAB Robotics Toolbox 的机器人学仿真实验教学[J].计算机教育,2010,(19):140-143.

[7]张刚,黄海波.HP20机器人的运动学逆解计算及模拟仿真[J].轻工机械,2011,29(6):40-45.

[8]孙浩,赵玉刚,姜文革,等.码垛机器人结构设计与运动分析[J].制造业自化,2013,(14):66-68.

[9]刘萍,陈莹.五自由度关节式机械手运动学分析及仿真[J].制造业自动化,2011,(19):9-11.

[10]张普行,严军辉,贾秋玲.六自由度机械手的运动学分析[J].制造业自动化,2011,(20):68-71.

[11]MAYROGA R V，SANONGBOOM . A radial basis function network approach for geometrically bounded manipulator inverse kinematics computation[J]/ /2003 IEEE/RSJ International Conference on Intelligent robots and system，2003，4(12):3564-3569.

[12]DENAVIT J，HARTENBERG R S. A kinematic notation for lower-pair mechanisms based on matrices[J]. ASM Journal of Applied Mechanics，1955，22(2):215-221.

[13]TAROKH M，KIM M. Inverse Kinematics of 7-DOF Robots and Limbs by Decomposition and Approximation[J]. IEEE Transaction on Robotics，2007，23(3):6-11.

Solution for Inverse Kinematics and Research for the Singularity of the 6R Robot

LIU He，LIU Lei，ZENG Hui，LI Xun，WAN Jun

(Anhui Efort Intelligent Equipment Co., Ltd， Academician Station Of Cai He-gao, Wuhu 241009, China)

Abstract:Aiming to solving the problem of computing complex and a lot of solutions in the solution process of inverse kinematics of robot,a geometric algorithm method for inverse kin-ematics of 6R manipulators is presented. The geometric algorithm method and dual variable tangent function are used to avoid losing solutions. The shortest distance rule of consecutive interpolation and the optimization flag are presented to choose a solution closest to the current manipulator for a number of inverse kinematics solutions. Additionally, singularity is avoided. The research results have been applied successfully in 6R robots of the company.

Key words:industry robot; inverse kinematics; singularity; consecutive interpolation

中图分类号：TP24

文献标志码：A

文章编号：1001-2443(2016)02-0132-05

作者简介：柳贺(1981-)，男，高级工程师，硕士，研究领域：机器人运动控制，工业控制总线等.

基金项目：安徽省工业机器人成套技术开发与应用项目(11Z0101010)和国家科技部863计划(2014AA041601).

收稿日期：2014-09-27

DOI：10.14182/J.cnki.1001-2443.2016.02.007

引用格式：柳贺，刘蕾，曾辉，等.6R机器人运动学分析及奇异处理研究[J].安徽师范大学学报：自然科学版，2016，39(2)：132-136.