粗糙集和MPGA在变压器故障诊断中的应用



粗糙集和MPGA在变压器故障诊断中的应用

0引言

变压器的运行状态对电网的安全影响很大。运用故障诊断，可以及时查出内部的早期故障，制定检修计划。油中溶解气体分析法(dissolved gas analysis，DGA)是变压器最常用的状态监测方法。但是，这种方法不仅会造成数据冗余，而且还会漏采，使数据的完备性、连续性变差。粗糙集理论能在处理不完备信息的同时发掘其潜在规律，找出其中的隐含知识，因而可应用于变压器的故障诊断。

属性值约简是粗糙集算法的核心内容。传统的基于差别矩阵的约简方法能够得到全部的约简组合，但矩阵的维数呈指数增长，因而不适用于数据量大的属性约简[1]。

长期以来，许多人工智能算法被应用到粗糙集的属性约简，进而用于变压器故障诊断。文献[1]通过粗糙集对故障信息进行简化，再用支持向量机对其进行故障诊断，使诊断结果有很大改进。文献[2]采用粗糙集和RBF诊断模型，提高了神经网络的收敛速度，改进了泛化能力。文献[3]通过标准遗传算法(standard genetic algorithm，SGA)对粗糙集属性进行约简，运用了SGA很强的局部搜索能力；但是SGA容易早熟收敛，常常不能得到理想的结果。文献[4]用自适应遗传算法，使得诊断效果大大提升；但算法模型不够完善，遗传参数需要根据经验试探性地给出，不恰当的设定会极大地影响最终效果。

本文首次将多种群遗传算法应用在粗糙集的属性约简,通过多个设有不同遗传参数的种群协同进化，各个子种群通过移民算子进行信息交换，维持着种群的多样性。通过人工选择算子，选出各个种群最优值，放入精华种群加以保存；对精华种群进行保护，以加快收敛速度。

1粗糙集相关理论

在本文的算法中，用到的粗糙集相关理论如下。

定义1(决策表)：S={U,A,V,f}。其中U为论域，是所有对象的集合；A为属性集合,A=C∪D,A∪D,C为条件属性,D为决策属性；V属性代表属性的值域；f为信息函数，f:U×A→V,它指U中每一个对象x的属性值。

定义2(知识约简)：P和Q为定义在U上的两个等价关系簇。若P的Q独立子集S⊂P，有POSS(Q)=POSP(Q),则称Q为P的Q约简。约简的结果可能不是唯一的。其中,POSR(Q)表示由知识R判断肯定属于X的对象所组成的最大集合，也称为Q的正域。

定义3(核)：核为所有约简的交集，记作CORE(C)=RED(C)，表示属性集合C中包含所有约简的属性集合。核一定是唯一的，但有可能是空的。

定义4(属性相关度)：条件属性子集P⊆C与决策属性D的相关程度[5]。

(1)

式中:cad(*)为集合(*)中元素的个数；POSPD为那些可以根据属性子集P正确分类的对象。

2基于多种群遗传算法的粗糙集属性约简

2.1多种群遗传算法概述

多种群遗传算法是利用并行遗传的思想，将种群划分成N个子种群，而各子种群分别取不同的遗传参数独立进化[6]。每进化一代，子种群之间通过移民算子进行信息交换，然后通过人工选择算子选出最优个体放入精华种群。精华种群不进行选择、交叉、变异等遗传操作，以保证最优个体不被破坏。这样不仅能保证各个种群的多样性，还能抑制早熟。算法结构示意图如图1所示。

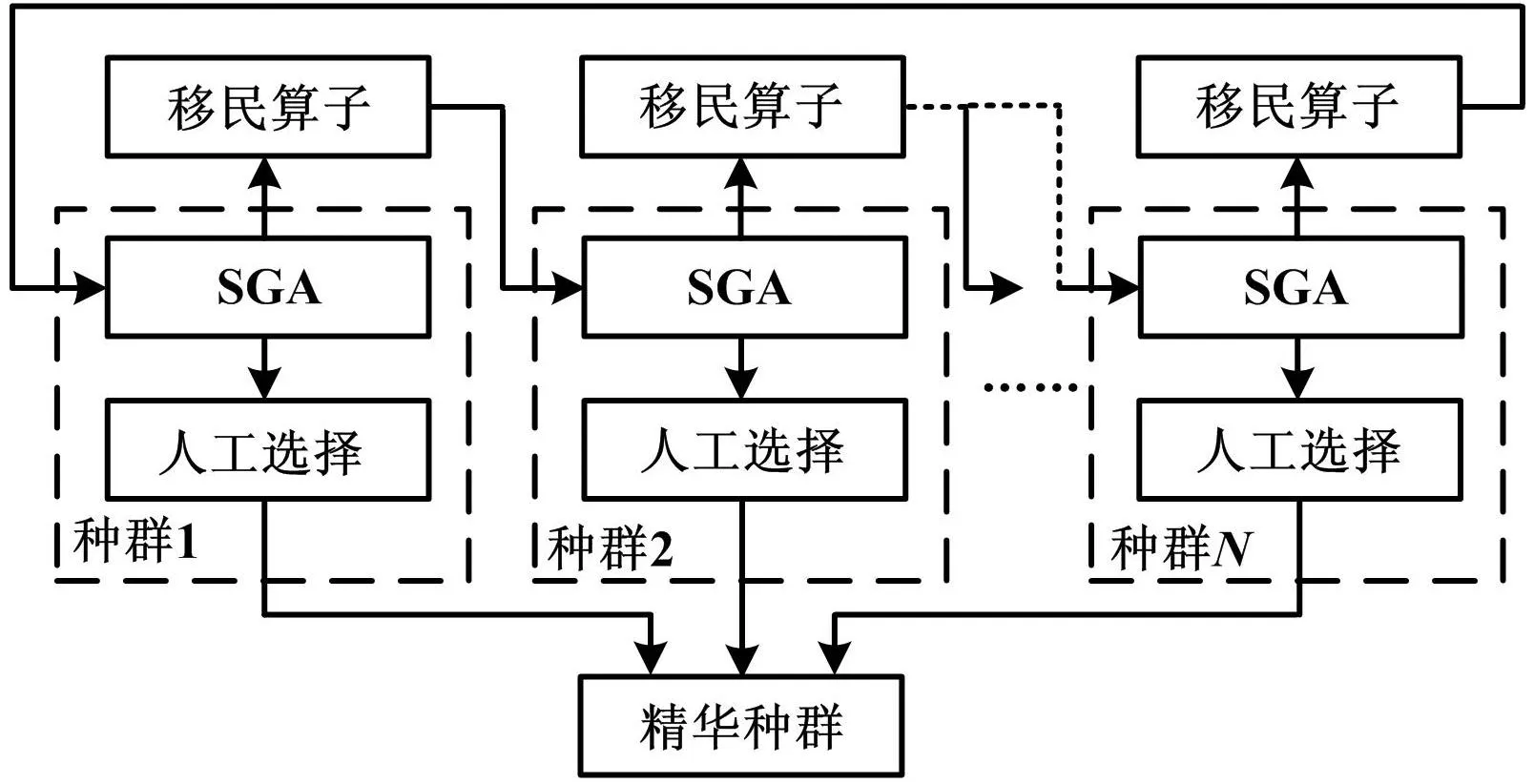
图1　多种群遗传算法结构示意图

2.2算法的具体步骤

本算法的具体步骤如下，流程图如图2所示。

第1步：输入粗糙集决策表S+{U,A,V,f}和算法的初始参数。其中,gen表示最优个体的保持代数,其初始值设定为0，然后设定一个gen的固定值Maxgen作为判定算法是否终止的条件，也就是最优个体的最大保持代数。

第2步：产生初始种群Pop(t)(t=1)。随机生成N个子种群，每个子种群有n个染色体。染色体采用二进制编码，并且长度和条件属性的个数相同。1代表这条属性被选中，0代表没被选中。染色体中必须包含核值所对应的属性。

第3步：确定适应度函数。本文采用的适应度函数是：

(2)

第4步: 判断进化是否结束(即判断gen是否大于Maxgen)。如果gen大于Maxgen，转入第10步；否则，转入第5步。

第5步：选择。选择用标准遗传算法中的轮盘赌方法。适应度值越高的个体进入下一代的可能性也就越大。

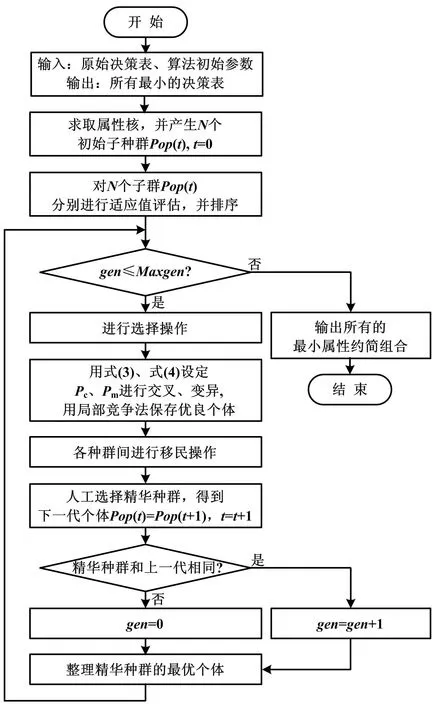
图2　算法流程图

第6步：交叉、变异。为模拟不同的进化条件，各子种群取不同的控制参数。交叉算子决定其全局搜素能力；变异算子决定其局部搜索能力。各子种群的交叉概率Pc和变异概率Pm在一定范围内随机产生：

Pc=Pc1+(Pc2-Pc1)k

(3)

Pm=Pm1+(Pm2-Pm1)k

(4)

式中：Pc、Pm为一个N维数组；Pc2、Pc1分别为N个子种群交叉概率的上下限；Pm2、Pm1分别为变异概率的上下限;k=rand(N×1)为一个N维数组，其元素数值介于0到1之间。

在进化的后期，个体适应度可能会降低，在交叉变异等遗传过程中种群可能会丢失当前最优个体，出现逆向进化的现象。本文用局部竞争法解决这个问题。所有的个体进行交叉后，均要与其父代比较适应度，适应度大的作为下一代保留下来，适应度小的淘汰。同样的方法用于所有的个体进行变异后。这种方法要优于文献最优个体保存法，因为它不仅保存了当前最优个体，还让当前最优个体进一步改进成为了可能，使得算法能够更好地进行粗糙集属性约简。方法具体流程如图3所示。

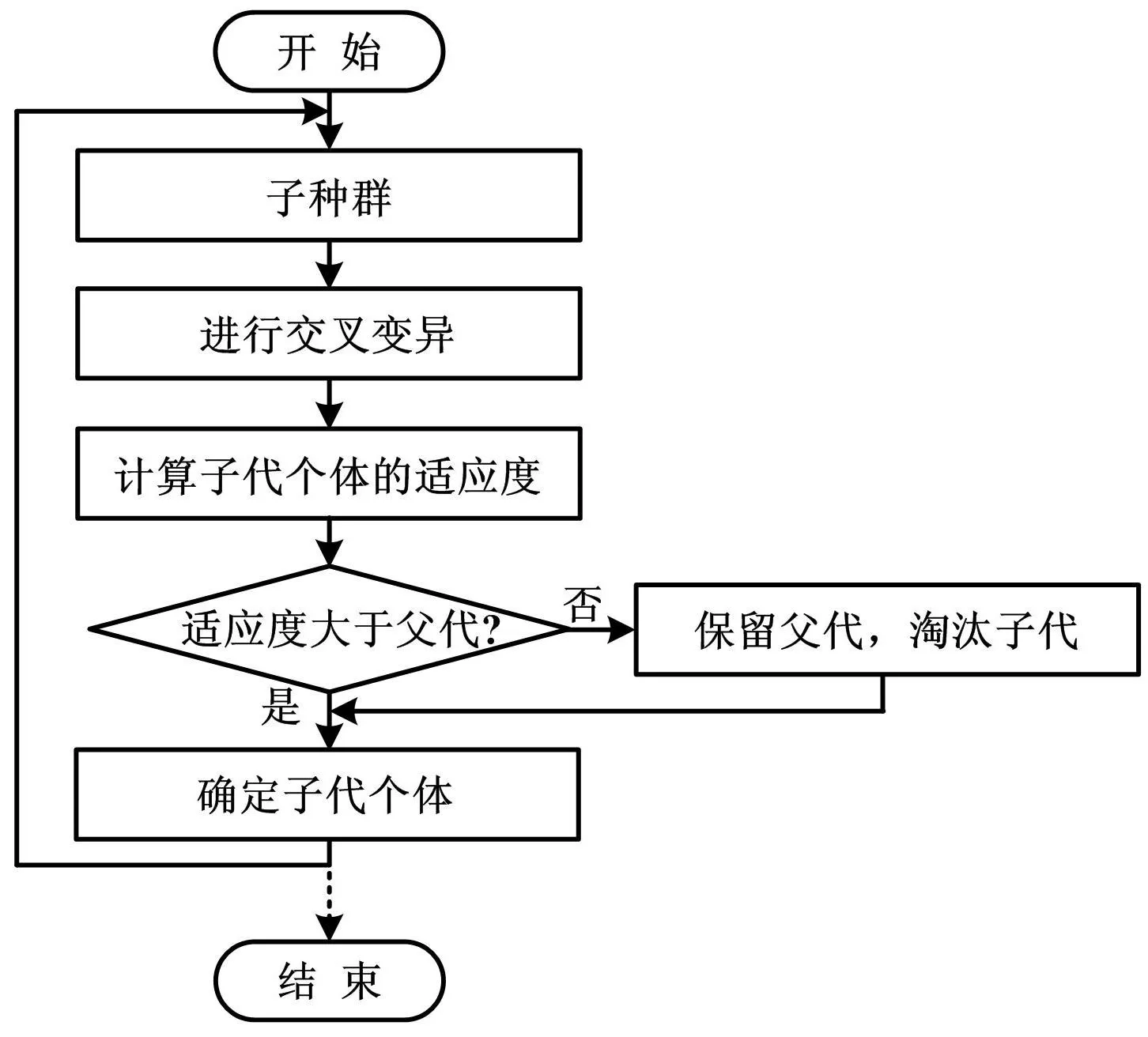
图3　局部竞争法结构图

第7步：进行移民操作。将各种群出现的最优个体引入到其他种群中，来替换其他种群适应度最差的个体。

第8步：人工选择精华种群。将各子种群的适应度最高的个体保存在精华种群中。

第9步：判断精华种群是否和上一代相同。如果相同，则gen=gen+1。如果不相同的话，更新精华种群，然后令gen=0。最后将精华种群中的最优个体整理出来，转第4步。

第10步：输出所有的最优个体，即最小条件属性组合。

3变压器故障诊断

针对文献[8]关于变压器的历史故障数据表，表中列举了29个样本，其中包括3个正常状态、6个低能放电、6个高能放电、6个中低温过热及8个高温过热。上述每一类状态分别用1到5编号。其中，前15列为条件属性，分别是C2H2/H2、C2H4/H2、C2H6/H2、CH4/H2、CH4/总烃、C2H4/总烃、C2H6/总烃、C2H2/总烃、C2H2/ C2H4、C2H4/ C2H6、C2H6/ CH4、CH4/ C2H4、C2H2/ C2H4、C2H2/ C2H6、H2/(总烃+ H2)；最后一列(即第16列)为决策属性。最后，采用基于差别矩阵[9]的方法进行离散化，得到离散化决策表。

在进行仿真实验时，本文选择参数：N=5，n=40，Pc2=0.9，Pc1=0.8，Pm2=0.09，Pm1=0.02，Maxgen=10。仿真结果如图4所示。其中，图4(a)为标准遗传算法的进化过程图，图4(b)为采用多种群遗传算法的进化过程图。

图4　两种遗传算法进化过程图

由图4(a)可知，标准遗传算法到20代依然没有得出所有的最小属性约简表，而且每一代的结果都起伏不定，收敛性极差，说明标准遗传算法容易陷入局部最优值，不能得到所有的最小约简组合。由图4(b)可知，在多种群遗传算法中，到第二代就得到了所有的15组约简表，并且一直不变，收敛性极好。这15个决策表分别是(C7,C14,C15)、(C6,C11,C14)、(C6,C11,C13)、(C6,C7,C13)、(C2,C7,C13)、(C4,C7,C14)、(C7,C8,C15)、(C6,C7,C8)、(C4,C7,C8)、(C4,C7,C13)、(C2,C7,C14)、(C6,C7,C14)、(C2,C7,C8)、(C7,C13,C15)、(C6,C8,C11)。从这15个决策表中提取出诊断规则，与文献[8]中的结果相同。

为了便于与文献[10]中提到的传统诊断方法进行比较，同样选取文献[11]中35组数据作为测试数据，并用等频率离散化[12]方法进行离散化。其中，包括5组正常状态、5组低能放电、5组中低温过热、9组高能放电、11组高温过热。用多种群遗传算法进行故障诊断，并与BP神经网络、单一的粗糙集的诊断结果进行对比，如表1所示。

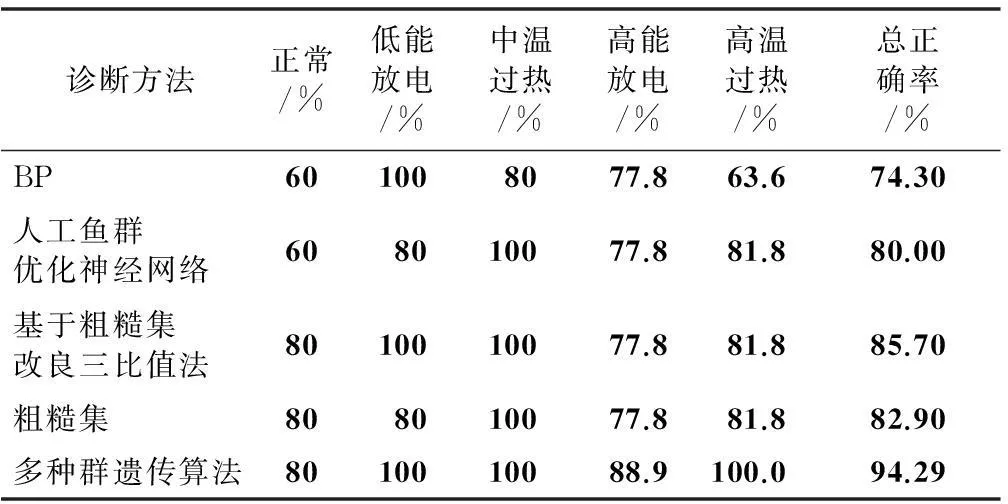
表1　各方法的变压器故障诊断准确率

由表1可以看出，多种群遗传算法在低能放电、中温过热和高温过热3种状态的正确率为100%，在正常和高能放电两种状态下各出现一个错误。在正常状态下诊断，该方法的正确率是80%，相对于BP和人工鱼群优化神经网络有较大的提升。和基于粗糙集改良三比值法和粗糙集法一样，错误可能是由于个别故障特征数据异常造成的。在高能放电状态下，该方法的诊断正确率是100%，与其他4种方法相比有很大的提升。多种群遗传算法的总体正确率为94.29%，远远高于其他4种方法，说明该算法实际应用到变压器故障诊断中，具有一定的可行性。

4结束语

本文采用多种群遗传算法，对粗糙集进行属性约简，建立了一种混合智能算法的诊断模型。虽然属性约简结果和文献[8]相同，但所采用的混合智能算法更具优越性。首先，通过多个种群协同进化以及移民算子来保持种群多样性，通过在一定范围内随机选取遗传参数，克服了文献[8]中凭借人工经验选择参数的缺陷；其次，采用局部竞争法，不仅保存了最优个体，还让其有进化的机会，加快了属性约简的速度。这些方法的应用，使得多种群遗传算法对粗糙集属性约简时能得到所有的最小属性约简组合，并且快速收敛。

参考文献

[1] 蒋延军,倪远平.基于粗糙集与支持向量机的变压器故障诊断法[J].高电压技术，2008,34(8):1755-1760.

[2] 杨志超，张成龙，吴亦，等.基于粗糙集和RBF神经网络的变压器故障诊断方法研究[J].电测与仪表,2014，51(21):34-39.

[3] 李伟生,易哲.基于遗传算法的粗糙集属性约简[J].微电子学与计算机,2010,27(3):71-74.

[4] 朱继,喻瑛,王辰炜,等.基于粗糙集和自适应遗传算法的电力变压器故障诊断[J].2012,49(558):47-51.

[5] 周献中，黄兵，李华雄，等.不完备信息系统知识获取的粗糙集理论与方法[M].南京：南京大学出版社，2010:19-21.

[6] 史峰,王辉,郁磊,等.Matlab智能算法30个案例分析[M].北京：北京航空航天大学出版社，2011:69.

[7] 冯超，周步祥，林楠，等.电动汽车充电站规划的多种群混合遗传算法[J].电力系统及其自动化学报,2013,25(6):123-129.

[8] 朱继，基于粗糙集的变压器故障诊断研究[D].上海：上海大学，2013.

[9] 陈静华，李小民.一种基于差别矩阵的粗糙集连续属性离散化算法[J].现代电子技术，2010(24):136-138.

[10]陈小青,刘觉民.采用人工鱼群优化粗糙集算法的变压器故障诊断[J].高电压技术,2012,38(6):1406-1407.

[11]徐永建.变压器故障诊断技术研究[D].南京：南京理工大学，2010.

[12]高意.基于差分演化算法的粗糙集离散化及属性约简的研究[D].长沙：长沙理工大学，2011.

Application of Rough Set and Multiple Population Genetic Algorithm in Fault Diagnosis of Transformer

黄伟赵寅邦

(上海电力学院自动化工程学院，上海200090)

摘要：标准遗传算法(SGA)经常早熟并且收敛慢，在用于粗糙集属性约简时，往往只能得到部分最小条件属性组合，并且很难收敛。针对传统遗传算法的这些缺陷，采用多种群遗传算法(MPGA)，用移民算子、局部竞争法来保持种群的多样性，以防止其陷入局部最优。将多种群遗传算法用于粗糙集属性约简，可得到所有的最小条件属性组合，并且收敛速度快。实例应用验证了该算法的有效性，可用于变压器的故障诊断。

关键词：人工智能算法标准遗传算法故障诊断变压器粗糙集多种群移民算子神经网络

Abstract：Standard genetic algorithm(SGA) is always early-maturing and slowly converging; what’s more,it gets only part of the minimum condition attribute combination and is difficult to converge when used for rough set attribute reduction.In order to solve these problems in traditional genetic algorithm,the multiple population genetic algorithm(MPGA) is used.Immigration operator and local competition are used to maintain the diversity of population and avoid falling into local optimal value.When MPGA is used for rough set attribute reduction,it can fast get all the minimum combination of condition attributes and converge in high speed.The practical examples verify that the algorithm is effective,and can be applied to the fault diagnosis of transformer.

Keywords:Intelligence artificial algorithmStandard genetic algorithm(SGA)Fault diagnosisTransformerRough setMultiple populationImmigration operatorNeural network

中图分类号：TP212;TH86

文献标志码：A

DOI:10.16086/j.cnki.issn1000-0380.201604006

上海市电站自动化技术重点实验室基金资助项目(编号：13DZ2273800)。

修改稿收到日期：2015-10-03。

第一作者黄伟(1966-)，女，1990年毕业于湖南大学自动化专业，获硕士学位，副教授；主要从事电站顺序控制与保护、电气设备状态监测与故障诊断方向的研究。