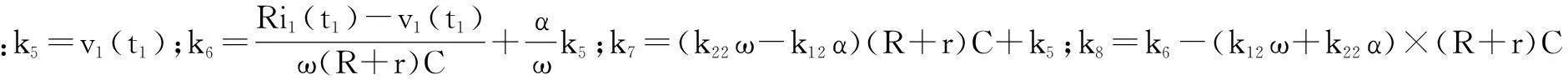电感与负载对V2控制Buck变换器的动力学影响
电感与负载对V2控制Buck变换器的动力学影响
0引言
微处理器电子设备要求电源模块具有快速的负载瞬态响应速度,而传统的电压型[1]和电流型[2]PWM控制技术,因负载响应速度慢而无法满足其负载响应速度要求。文献[3]提出了V2控制技术,利用输出电容等效串联电阻采样输出电容电流信息作为调制信号,大大提高了变换器的负载响应速度,可以满足微处理器对负载响应速度的要求。
现有文献[4]~[5]的研究表明,输出电容时间常数对V2控制开关变换器的稳定性有着很大的影响。当时间常数较大时,V2控制Buck变换器工作在稳定的周期1;当时间常数较小时,变换器工作在不稳定态。然而,当时间常数较小时,电感和负载电阻的变化将如何影响V2控制Buck变换器动力学行为,尚未有文献记载。
分岔分析可有效揭示开关变换器中存在的复杂非线性现象[6-9],以及参数变化对其动力学行为的影响。本文将通过建立V2控制Buck变换器的离散映射模型,利用Matlab仿真软件画出电感和负载电阻的分岔图,并分析其变化对变换器的动力学行为影响[10-11]。
1V2控制Buck变换器与离散映射模型
1.1工作原理
V2控制Buck变换器的电路原理图如图1所示。其中功率级电路由输入电压E、开关管S、二极管D、电感L、输出电容C及其等效串联电阻(equivalent series resistance,ESR)r和负载R组成;控制电路由误差放大器、比较器、RS触发器、时钟脉冲CP构成。在开关周期开始时,时钟信号使RS触发器输出VP为高电平,开关管S导通,二极管D关断,输出电压增加。当输出电压增加到控制电压vk时,开关管S关断,直至下一个开关周期开始。
输出电压v0由输出电容电压v及其ESR两端电压vr组成,且存在如下关系:
v0(t)=Hx=μ[v(t)+ri(t)]
(1)
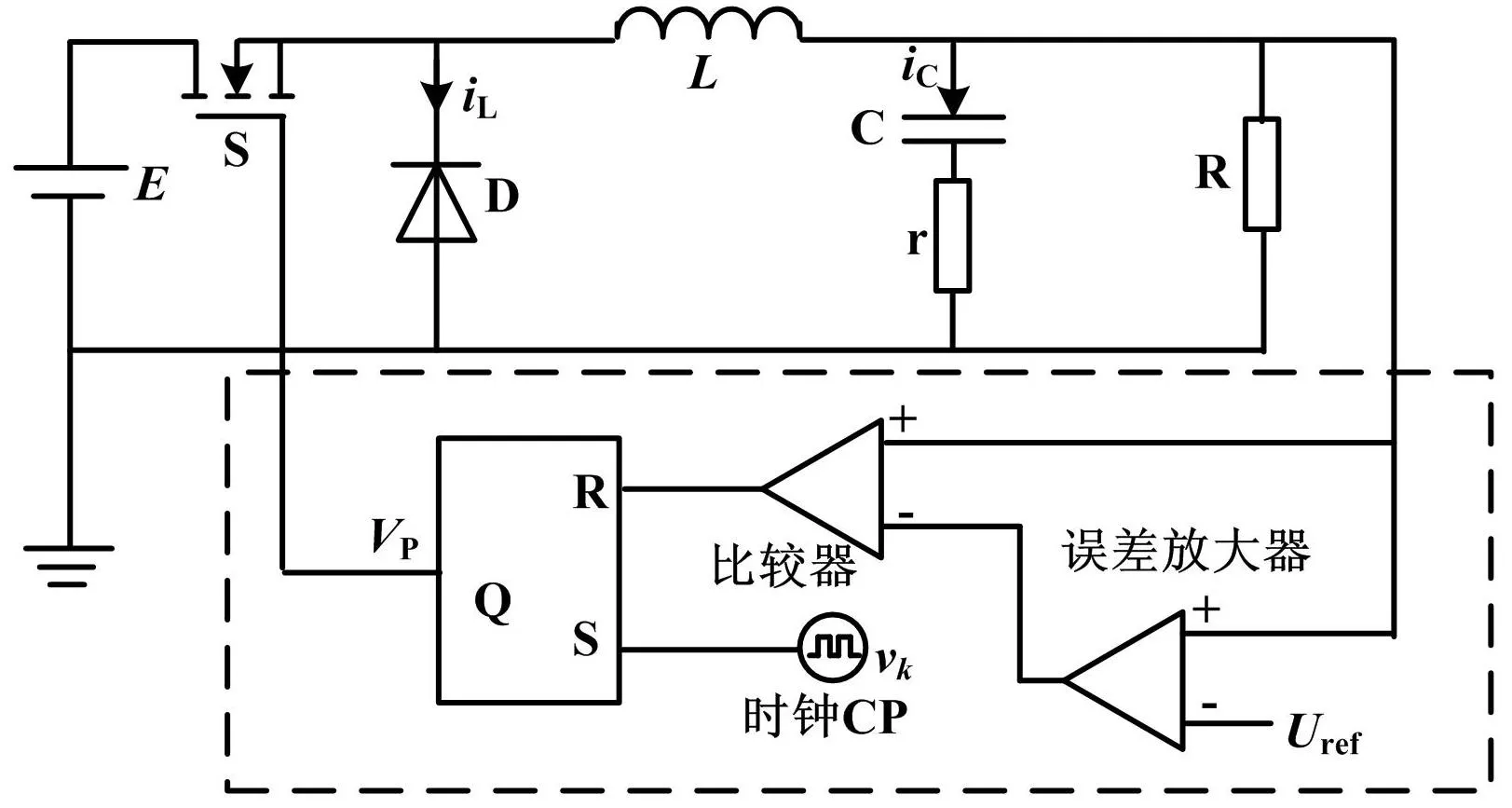
图1 V2控制Buck变换器示意图
1.2状态方程
根据开关管S和二极管D的不同工作状态,Buck变换器有3种工作模式[12]:工作模式1,S导通,D截止;工作模式2,S关断,D导通;工作模式3,S关断,D截止。当Buck变换器工作在连续导电模式(continuous conduction mode,CCM),仅存在工作模式1和工作模式2;当Buck变换器工作在断续导电模式(discontinuous conduction mode,DCM),3种工作模式均存在。在第n个开关周期T中,设工作模式1的持续时间为t1,工作模式2的持续时间为t2,工作模式3的持续时间为t3,对应的状态方程列写如下:
(2)
式中:A、B为系数矩阵。
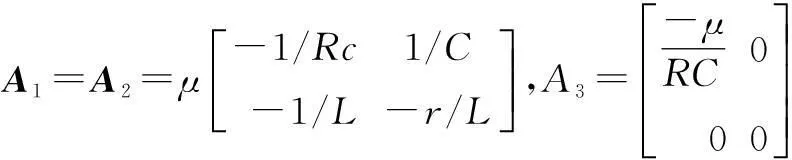

1.3离散映射模型
参照文献[4],设电容电压和电感电流在第n个开关周期初始值分别为vn和in。当变换器运行工作模式1时,由式(2)的第一个方程,可求得电容电压和电感电流的解分别为:
(3)
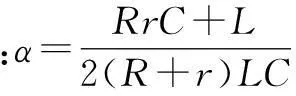

当t1>T时,在开关周期T内,变换器始终运行在工作模式1,此时将t1=T代入式(3),可求得V2控制Buck变换器的离散映射模型为:
(4)
当t1 (5) 将t=t2=T-t1代入式(5),得离散映射模型为: (6) 式中:t1由开关切换条件求得。 v0(t1)=vk(t1)=K[Vref-v0(t1)] (7) 当t1 (8) 将t=t3=T-t2-t1代入式(8),得离散映射模型为: (9) 式中:t1由式(7)求得;t2由开关切换条件i2(t2)=0求得。 综上,式(3)~式(9)构成了V2控制Buck变换器的离散映射模型。 2基于电感与负载电阻的分岔分析 基于第1.3节所建立的V2控制Buck变换器离散映射模型,分别以电感和负载电阻为分岔参数,研究其对V2控制Buck变换器动力学特性的影响。选取如表1所示的电路参数,其他参数保持不变,分别以电感L和负载电阻R为分岔参数的分岔图如图2和图3所示。值得强调的是,表1中输出电容时间常数较小[13]。 表1 V2控制Buck变换器电路参数 图2中,电感L的变化范围为50~200 μH。 图2 随电感L变化的分岔图 当电感L较小时,V2控制Buck变换器工作在稳定的DCM周期1;随着电感的增大,在L约为73 μH处,变换器发生一次倍周期分岔,其运行轨道由DCM周期1进入到DCM周期2;随着电感L的继续增大,在L约为133 μH处,变换器发生了第二次倍周期分岔,其运行轨道由DCM周期2进入DCM周期4;在L约为156 μH处,变换器发生了第三次倍周期分岔,其运行轨道由DCM周期4进入到DCM周期8;在L约为160 μH处,其运行轨道经边界碰撞分岔,由DCM周期8进入到DCM混沌;当电感增加到约为175 μH处,变换器的运行轨道由DCM混沌经第二次边界碰撞分岔进入到CCM混沌。 图3 随负载电阻R变化的分岔图 图3中,负载电阻R变化范围为2~10 Ω,当负载电阻R较小时,V2控制Buck变换器工作在不稳定的CCM混沌;随着R的增大,在负载电阻约为3 Ω处,经一次边界碰撞分岔,变换器的运行轨道由CCM混沌进入到DCM混沌;随着R继续增大,在R约为3.1 Ω处,变换器的运行轨道经第二次边界碰撞分岔,由CCM混沌态进入DCM周期8;随着R增大到约为3.2 Ω时,变换器发生了一次逆倍周期分岔,其运行轨道由DCM周期8进入DCM周期4;随着R进一步增大到约为3.7 Ω时,变换器发了第二次逆倍周期分岔,其运行轨道由DCM周期4进入到稳定的DCM周期2。在R约为6.8 Ω时,变换器发了第三次逆倍周期分岔,其运行轨道由DCM周期2进入到稳定的DCM周期1。 由以上分岔分析可知,当输出电容时间常数较小时,通过减小电感或增大负载电阻,可使V2控制Buck变换器工作在稳定DCM周期1。 3PSIM电路仿真验证 利用PSIM软件,搭建V2控制Buck变换器的仿真电路,选取表1所示的电路参数,进行电路仿真,以验证第2节分岔分析的正确性。 保持其他电路参数不变,不同电感和不同负载电阻时的仿真结果分别如图4和图5所示。图4(a)左侧为时域波形,包括电感电流i波形、输出电压v0波形和时钟脉冲VP波形;图4(a)右侧为i-v0平面上的相轨图。 图4 不同电感L对应的仿真结果 图4(a)中,L=65 μH,由时域波形和相轨图可以看出,V2控制Buck变换器工作在稳定的DCM周期1;图4(b)中,L=100 μH,变换器工作于不稳定的DCM周期2;图4(c)中,L=180 μH,变换器工作在不稳定的混沌状态。 图5(a)中,R=3 Ω,由时域波形和相轨图可以看出,V2控制Buck变换器工作在不稳定的混沌状态;图5(b)中,R=6 Ω,变换器工作于不稳定的DCM周期2;图5(c)中,R=8 Ω,变换器工作在稳定的DCM周期1。 图4和图5所采用的电路参数值,分别对应图2和图3中相应的典型参数值。对比仿真波形和分岔图可以看出,电路仿真结果很好地验证了分岔分析的正确性。 图5 不同负载电阻R对应的仿真结果 4结束语 基于建立的V2控制Buck变换器离散映射模型,本文通过分岔分析揭示了输出电容时间常数较小时随着电感的增大或负载电阻的减小,V2控制Buck变换器具有从稳定DCM周期1经倍周期分岔、边界碰撞分岔进入到CCM混沌态的分岔路由。PSIM电路仿真结果验证了分岔分析的正确性。研究结果表明,当输出电容时间常数较小时,可通过选择较小的电感或较大的负载电阻使V2控制Buck变换器工作在稳定DCM周期1状态。本文的研究结果对V2控制Buck变换器的电路设计和参数选择具有重要的指导意义。 参考文献 [1] 罗辞勇,肖发福,唐书窗.电压模式Buck变换器混沌建模与控制研究 [J].计算机仿真,2014,31(9): 151-155. [2] Bao B C,Zhou G H,Xu J P,et al.Unified classification of operation-state regions for switching converters with ramp compensation [J].IEEE Transactions on Power Electronics,2011,26(7):1968-1975. [3] Goder D,Pelletier W R.V2 architecture provides ultra-fast transient response in switch power supplies [C]//Proceedings of HFPC Conference,1996: 19-23. [4] 何圣仲,周国华,许建平,等.输出电容时间常数对V2控制Buck变换器的动力学特性的影响 [J].物理学报,2014,63(13):25-36. [5] Zhou G H,He S Z,Zhang X,et al.Critical output-capacitor ESR for the stability of V2 controlled buck converter in CCM and DCM [J].Electronics Letters,2014,50(12): 884-886. [6] Xie F,Yang R,Zhang B.Bifurcation and border collision analysis of voltage-mode-controlled flyback converter based on total ampere-turns [J].IEEE Trans.Circuits and Systems I:Regular Papers,2011,58(9):2269-2280. [7] 石季英,潘如政,段大鹏,等.软开关Buck变换器混沌现象的研究 [J].计算机仿真,2006,23(4):309-313. [8] 雷涛,林辉,张晓斌,等.DC-DC功率变换器中非线性的仿真研究 [J].计算机仿真,2008,25(4):308-312. [9] 包伯成,许建平.开关变换器周期窗内吸引子共存现象仿真工作研究 [J].计算机仿真,2009,26(1):248-255. [10]赵益波,罗晓曙,方锦清,等.电压反馈型DC-DC变换器的稳定性研究 [J].中国原子能科学研究院年报,2005,54(11):5022-5026. [11]吴志敏.脉冲序列控制DCM Boost变换器的稳定性分析 [J].计算机仿真,2014,31(7):127-131. [12]包伯成,杨平,马正华,等.电路参数宽范围变化时电流控制开关变换器的动力学研究[J].物理学报,2012,61(22):220502. [13]张希,许建平,包伯成,等.固定关断时间控制Buck变换器斜坡补偿技术及其机理研究[J].中国电机工程学报,2014,34(36):6426-6434. Dynamics Effects of Inductance and Load on V2-controlled Buck Converter 史国栋1杨艳1张希2吴志敏1包伯成1 (常州大学信息科学与工程学院1,江苏 常州213164;西南交通大学电气工程学院2,四川 成都610031) 摘要:在连续导电模式(CCM)时,V2控制Buck变换器的控制性能主要取决于输出电容的时间常数。基于离散映射模型,利用分岔图研究了输出电容时间常数较小时,电感与负载电阻对V2控制Buck变换器的动力学特性影响。结果表明,当时间常数较小时,V2控制Buck变换器工作在断续导电模式(DCM)次谐波或CCM混沌振荡状态,通过选择较小的电感或较大的负载电阻,该变换器将工作在正常的DCM周期振荡状态。PSIM电路仿真验证了分岔分析的正确性。 关键词:Buck变换器V2控制电感负载电阻连续导电模式(CCM)断续导电模式(DCM)Matlab离散映射 Abstract:When operating in continuous conduction mode(CCM),the control performance of V2-controlled buck converter mainly depends on the time constant of the output capacitor.Based on the discrete mapping model,the dynamics effects of inductance and load resistance on characteristics of V2-controlled buck converter with small time constant output capacitor are investigated by using the bifurcation diagrams.The study results indicate that when the time constant is small,V2-controlled buck converter operates in discontinuous conduction mode(DCM) subharmonic or CCM chaotic oscillation states,through selecting smaller inductance or bigger load resistance,the converter will operate in normal DCM periodic oscillation state.PSIM circuit simulations verify the validity of bifurcation analysis. Keywords:Buck converterV2-controlInductanceLoad resistanceContinuous conduction mode(CCM)Discontinuous conduction mode(DCM)MatlabDiscret mapping 中图分类号:TP391;TH82 文献标志码:A DOI:10.16086/j.cnki.issn1000-0380.201604003 国家自然科学基金面上基金资助项目(编号:51277017); 常州市基础研究计划自然科学基金资助项目(编号:CJ20159026)。 修改稿收到日期: 2015-08-03。 第一作者史国栋(1956-),男,2006年毕业于南京理工大学电气自动化专业,获硕士学位;教授;主要从事电气自动化与应用、人工智能等方向的研究。