电磁感应位移传感器耦合天线的设计研究



电磁感应位移传感器耦合天线的设计研究

0引言

通过LC谐振器与收发天线电磁耦合实现位移测量的传感技术，是基于电感式位移传感器原理的革新技术[1]。这种类型的传感器能通过控制激励信号频率实现多个目标物的高速测量，并激励信号在兆赫数量级，通过低通滤波器的截止频率值高于线性可变差动变压器(linear variable differential transformer,LVDT)传感器，以此来提高系统响应[2]。它的测量盲区短，在低成本、小型化的传感器中能很好地替代LVDT和磁致伸缩式位移传感器。由于通过检测LC电路来工作，因此该传感器不受磁场干扰影响，具有极好的EMC特性，使变频器、大电机、铁磁性金属或永磁体的干扰都不再是问题。这种特性优于LVDT、感应同步器、电容传感器、基于霍尔效应的直线位移传感器。此外，这种传感技术不同于电容式和光学技术，它具有很强的鲁棒性，通常对极端温度、湿度、机械错位、直流、交流场下的适应性强；具有对高精度的机械装配要求不高、不易受水凝物与灰尘影响等优势。这个特点使得这种新型电磁感应式位移传感器广泛应用于机床、计量系统、包装机、风力涡轮机或行程与定位控制系统等[3]。

本文主要介绍了电磁感应式位移线性传感器的结构设计，根据电磁理论推导天线耦合系统电磁分布数值表达式，并利用Matlab绘制模型系统空间点的电磁场分布，验证天线电磁耦合系统工作原理的正确性与可行性。对天线模型电磁场，运用Ansoft Maxwell三维电磁仿真软件分析系统关键参数对输出的感应信号的影响，并给出合理优化的结构参数，为这种高频非接触电磁式位移传感器的开发和应用提供有益的参考。

1传感器的原理及结构

传感天线的结构如图1所示，包括固定部件与移动部件。固定部件为印刷电路板，上面分布着分别成正、余弦变化的激励天线和接收长直天线[4]。移动部件为一个无源的LC谐振器。由交变的电磁场激发产生振荡电路。沿着X轴向移动，由于振荡交变电路产生的交变磁场削弱原磁场的作用，在感应线圈能感应出场强变化位置的电信号，由此来指示位移的变化[5]。

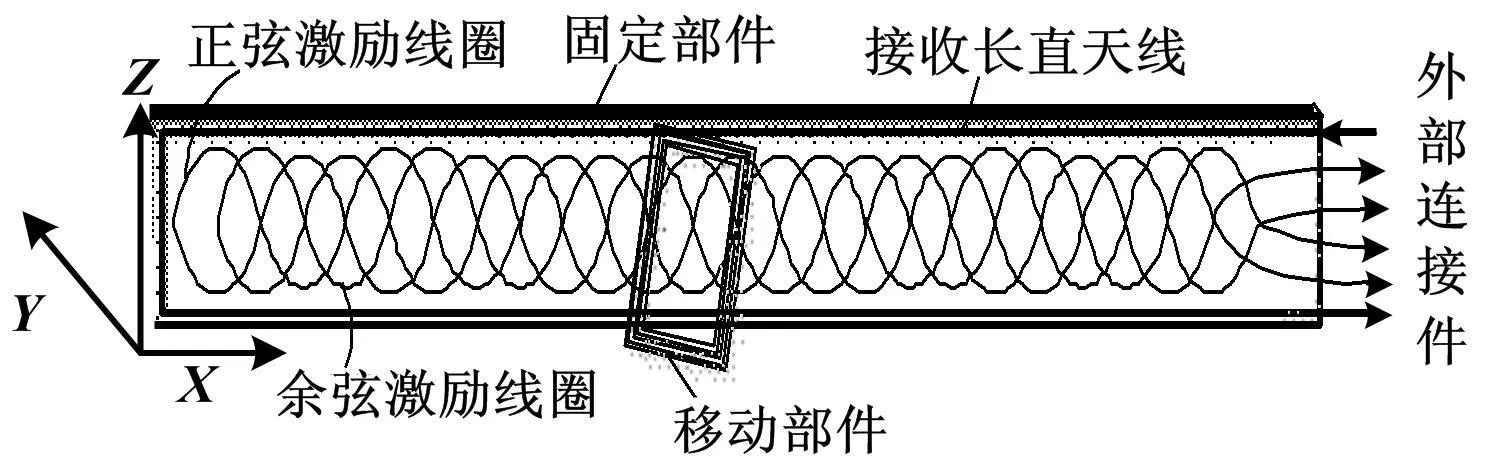
图1　传感器结构示意图

由于激励线圈电流成正反依次分布。当激励线圈通入高频交流电时，在激励线圈附近产生的交变磁场是均匀分布的，未采用移动谐振器时，在接收线圈中感应电动势也是正负相互抵消。此时感应线圈输出的电压为零。只有当谐振器位于天线板上方移动时，高频激励信号对LC谐振线圈的涡流效应使得谐振器线圈中产生了同频的交流电；同时，谐振器反过来产生交变磁场，同样作用于感应接收线圈产生了只随谐振器位置变化的感应交流电。

1.1激励线圈空间电磁分布

上下两个正弦天线线圈形成闭环回路。当正弦激励天线通以交流电时，在其周围产生交变磁场。根据线圈毕奥-萨伐尔定律：

(1)

式中:I为通电电流;Idl为电流元;R为电流源到场点的距离。

周期性变化的线圈是由y=sinx和y=-sinx构成的极性相反的闭合天线，对于y=sinx变化的线圈R[(X1-t,Y1-sin(t)，Z1],dl=[ex,cos(t)ex,cos(t)ey,0]dt。

(2)

而对于y=sinx变化的线天线圈，有R=[X1-t,Y1+sin(t)，Z1],dl={[ex,cos(t)ey,0]}dt,dl=[ex,cos(t)ex,cos(t)ey,0]dt。

(3)

所以，一组正反正弦变化的天线线圈产生的磁感应强度的表达式为：

Bsin=B1+B2

(4)

同理可得，余弦天线线圈在空间点产生的磁感应强度为：

(5)

(6)

因此，正反余弦变化的天线线圈产生的磁感应强度为几组线圈磁场的叠加：

(7)

当y=0时，中心轴线上方x和y方向的磁感应强度与z方向的磁感应强度相比只有较小的分量，所以线圈产生的磁感应强度近似于只有z方向的磁场，即垂直于天线平面的磁场。

利用Matlab仿真，在中心轴线上方Z=1平面的3个方向分量磁感应强度如图2所示。

仿真Z=1平面上的磁感应强度分布情况，B在x、y方向上的分量都很小，在0.1 t左右，相对于z方向上的磁感应强度可以忽略。且正弦线圈产生的磁场在平面上成正弦变化，余弦线圈产生的磁场在平面上成余弦函数变化。因此，正弦线圈与余弦线圈通电流时，在离天线板一定距离的中心轴线上的磁感应强度为：

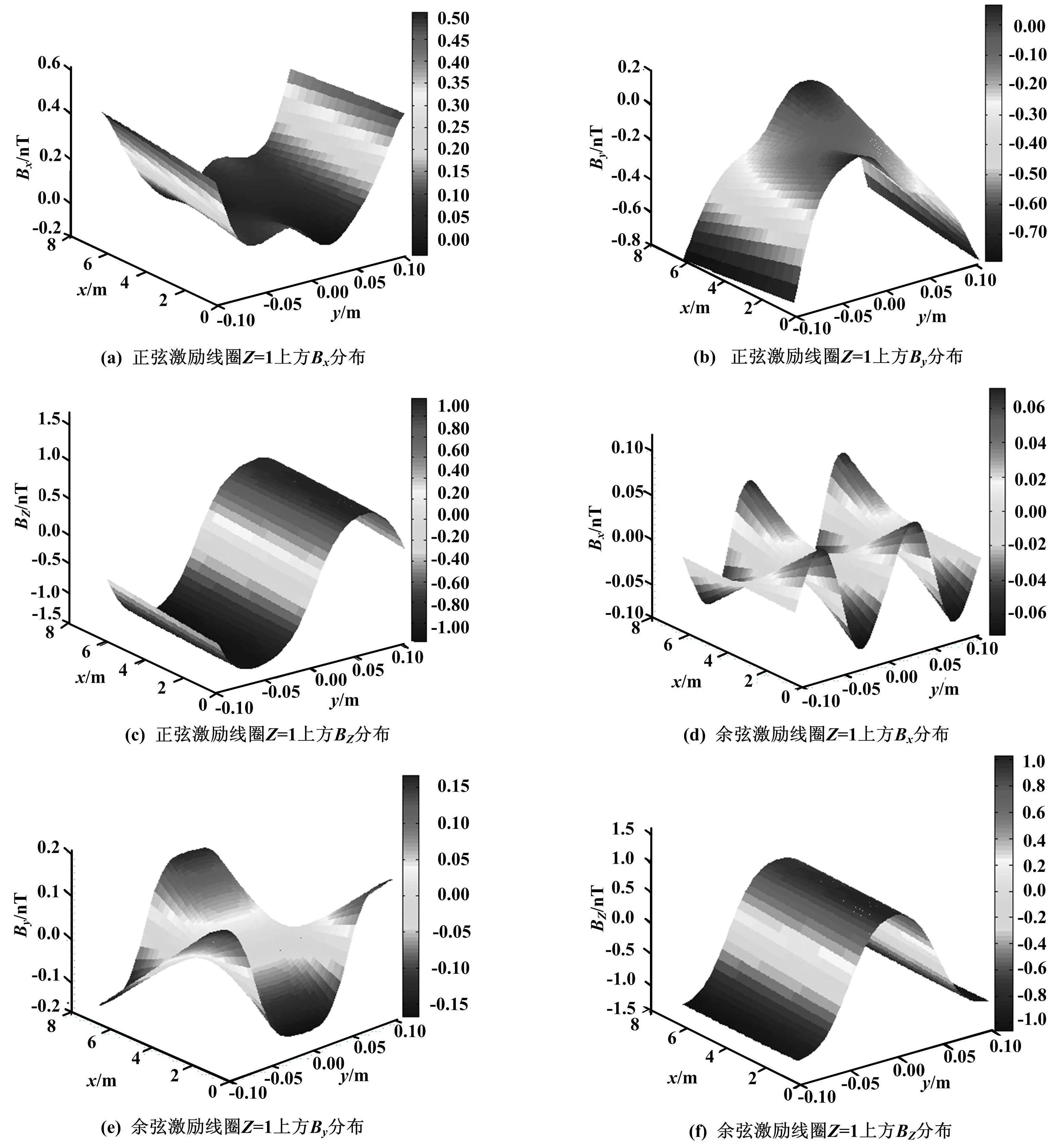
图2　3个方向磁感应强度示意图

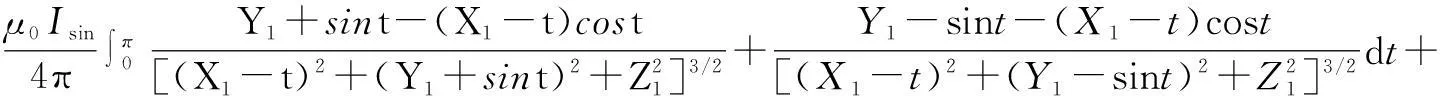
(8)

式中：L为正弦线圈一周期的直线长度。

当激励天线线圈中通以交变电流，线圈内部的磁场随时间变化将会有感生电场产生。由于感生电场也是随时间而发生变化的，因此将有附加磁场产生，感生电场和附加磁场依次交替产生。激励线圈内部的总磁场可以看作是励磁电流产生的磁场和一系列附加磁场的叠加。

假设激励线圈内部的磁场是分布均匀的，激励线圈内部的总磁场可表示为：

B(r,t)=B(r)ejωt=Bejωt

(9)

代入麦克斯韦方程组，可得到关于磁感应强度的亥姆霍兹方程：

(10)

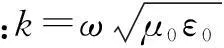
(11)

式中:r为z轴与激励线圈的轴线重合的圆柱坐标系的径向轴变量;A为积分常数;c为真空中电磁波的传播速度;ω为交变电流的角频率。当正弦激励线圈中通以稳恒直流电I时，有：

(12)

当正弦激励线圈通以交变电流ωr<

(13)

因此，当正弦和余弦线圈分别通以同频的正弦和余弦交流电时，在天线板上方中心轴线上产生的磁感应强度瞬时表达式为：

cos(2πx/L)cos(2πf0t)]=

(14)

1.2接收线圈感应电流的产生

正弦激励线圈产生的感应交流磁场为：

(15)

由其在LC谐振器线圈激发的感应交流电为：

(16)

式中：S1(x)=sin(2πx/L)。因此，稳恒LC谐振电路在其周围产生的磁场为：

(17)

K1与线圈的数量、半径等因素有关。根据法拉第电磁感应定律[7]，LC谐振器交变磁场在接收线圈中的感应电动势为：

(18)

式中:φ为通过单个回路中的磁通量;B为回路中的磁感应强度;ds为回路的回路元矢量。由接收谐振器在长直矩形线圈中沿中心轴线移动，ds为回路的回路元矢量且为一常数，感应电磁场在感应接收线圈只产生磁场随时间变化的感生电动势。因此，得到正弦线圈激励磁场通过LC振荡电路感应磁场Br在接收线圈中产生的感应电动势表达式为：

EMF1=2πf0K2I1S1(x)sin(2πf0t)

(19)

同理，余弦线圈激励磁场通过LC振荡电路感应磁场Br在接收线圈中产生的感应电动势表达式为：

EMF2=2πf0K2I1S2(x)cos(2πf0t)

(20)

式中:S2(x)=cos(2πX1/L)。两组激励线圈激发随LC振荡电路，对接收线圈中产生感应电动势为两者感应电动势的叠加值为：

EMF=2πf0K3cos(2πf0t-2πX1/L)

(21)

通过测量余弦激励信号与感应信号的相位差，即可得到LC谐振器在天线板轴线上的移动位置。

2Ansoft模型的建立及仿真

由于天线材质、谐振器在空间位置产生的涡流效应[6]，对谐振器平面磁场的分布以及谐振器和接收线圈感应电流很难做到精准求解。因此，借助有限元的方法，可以求得磁场在天线耦合系统中的分布情况，探究天线材质、谐振器与位移板相对高度以及谐振器移动时对输出感应信号的影响，从而确定合理、可行的传感元件结构参数[7]。

2.1系统模型的建立

天线电磁耦合系统是一个三维场，激励线圈信号为高频正弦交流电，利用Ansoft Maxwell 3D的瞬态电磁场，对天线板和谐振器进行三维建模。

(1)激励天线。

正余弦激励线圈为正余弦走向的单导体，导体半径为0.2 mm。激励线圈中间过孔连接，在PCB上下板分别形成正负单圈的闭合回路。板间距设为0.8mm。线圈类型设置为strands。

(2)感应天线。

感应线圈分布在距激励线圈轮廓2 mm外的矩形宽截面单导体，位于激励线圈同一块PCB板上。考虑到激励线圈的正负回路对接收线圈的具有相同的磁效应，因此接收线圈应位于正负板上的中间平面处，线圈宽度为0.2 mm。

(3)LC无源谐振器。

将LC无源谐振器简化为多匝矩形线圈。由于当激励线圈中通以高频交流电时，在LC振荡电路中能产生感应电流。这里的感应电路以涡流的形式出现，当设计LC谐振器的线圈时，应考虑导体能产生涡流效应的趋肤深度[8]，趋肤深度计算公式为：

(22)

根据式(22),可以看出在导体材料确定的情况下，正弦交流电频率值越大，趋肤深度越小，当激励交流电频率为0.1 MHz时，趋肤深度为0.21 mm，因此要保证接受线圈中信号的质量，LC谐振器线圈导体的厚度在趋肤深度附近有显著的电磁感应现象。

2.2仿真结果分析

2.2.1接收线圈中的感应电流

由于正、余弦激励天线具有相同且相互独立的电磁特性，因此简化模型，只仿真一组正弦天线激励线圈，相应的余弦线圈具有相同电磁场分布。考察没有谐振器移动物时，扫描求解的所有时间点解得的激励线圈在天线板附近-10～10 mm轴线范围的磁感应强度，电磁特性曲线如图3所示。

图3　电磁特性示意图

从图3(a)可知，在天线板平面附近激励线圈产生的磁场在中心点附近呈对称分布，在8～12 mm有明显的磁场变化。磁感应强度能达到9 mT，这是由于正弦线圈布线在中心点通孔使线圈部分下移导致磁场强度在中心点附近下移。当激励信号给电流峰值为8 A时，利用场计算器计算出在两个电周期内接受线圈中的感应电流，如图3(b)所示，电流最大幅值为0.4 mA，符合正弦变化形式。在没有谐振器作用时，在接收线圈中感应电流非常小，因此可以忽略激励线圈对感应线圈的直接影响。

2.2.2系统瞬时电磁场分布

天线板平面上瞬时磁感应强度的分布,在一个电周期10 μs内，PCB平面激励线圈感应强度也随激励交流电有相同的变化趋势(成正弦变化)；在t=5 μs时，激励线圈中的电流为0，谐振器中的感应电流对激发的磁感应强度最大。谐振器覆盖区域的磁感应强度为2×10-4T，感应线圈上的最大磁感应强度约为4×10-4T。观察谐振器平面上的电流密度在仿真周期内的变化，谐振器由于受到激励线圈的激励产生了感应电流，与激励线圈信号频率相同但有一定的相位差。在2 μs和 7 μs时，谐振器中的感应电流密度最大为1×107A/m2；在4.5 μs和9 μs时，谐振器中感应电流密度最小，在1.25×106A/m2左右。

应用场计算器计算接收线圈中随时间变化的如图4所示。得到感应电流在接收线圈中符合正弦变化，峰值电流为60 mA左右，频率与激励信号频率相同，但相对激励线圈有一定的相位延时，这与接收线圈材料线圈电感和结构相关。

图4　接收线圈中感应电流随时间的变化曲线图

2.2.3谐振器材料的影响

谐振器为导电材料，在激励高频信号的作用下产生涡流效应，而导磁材料在产生涡流效应的同时，还会导致传感器部分磁感应强度不均匀[9]。因此，表1对常见的几种金属材料，如铁、钢、铜、铝、坡莫合金进行了分析，比较不同材料对电磁耦合系统电磁场变化以及接收线圈中感应电流的影响。

表1　不同材料的电导率和相对磁导率

由表1看出：由于金属铝、铜电导率相对较大，作为谐振器的线圈在激励磁场作用下产生的涡流效应很明显，线圈中的电流密度相对较大，能达到1×107A/m2；但其相对磁导率较低，所以由谐振器交变磁场激发接收线圈产生感应电流相对较小，幅值在60 mA左右。金属铁、坡莫合金作为导磁材所产生的磁效应强于自身的涡流效应，不利于谐振器线圈信号的输出；但由于遮挡激励线圈产生的交变磁场，故在接收线圈中的感应电流也会相应增大。钢材料的电导率和相对磁场率都很小，所以产生感应电磁变化不明显。

2.2.4谐振器相对高度影响

考察谐振器距天线板平面相对高度变化对感应线圈电流的影响，仿真谐振器距天线板的高度以0.5 mm等间距增加时，谐振器平面的磁感应强度以及感应线圈中感应电流大小，仿真结果如表2所示。

表2　谐振器不同高度对电磁耦合系统的影响

由表2看出，随着谐振器与天线板相对高度的增加，谐振器磁感应强度会减小。这主要是由于随着谐振器随着天线板高度的增加，铝环和励磁线圈之间的磁链耦合将会减小，因此通过铝环的磁通量也会相应地减小。根据电磁感应定律，感应天线电磁耦合系统中，感应线圈中的电流也会相应地减小。考虑到结构装配和系统的稳定性，设定谐振器与天线板的高度为2～3 mm。接收线圈中的电流为30 mA左右。

2.2.5系统工作时感应电流

分析谐振器运动时相对于天线板的位置与接收线圈中电流幅值变化的关系，从而在对感应线圈中的电信号进行分析与处理提取位移相关的信号值。对系统模型，在-35～35 mm轴线上采样15个点，模拟谐振器在天线板平面上的横向移动。

利用场计算器计算当谐振器在等距移动的位置时，激励电信号在周期内的接收线圈中的感应电流变化。根据仿真数据描点绘制，在电信号周期内谐振器移动位置与接收线圈感应电流的变化曲线如图5所示。

图5　谐振器不同位置接收线圈中的感应电流变化示意图

分析结果表明，接收天线线圈中的感应电流为激励信号同频的高频交流电，当采用铝金属作为谐振器线圈材料时，感应交流电峰值在60 mA左右。同时，电周期在同一时刻，接收天线中的感应电流幅值大小随移动谐振器的位置近似呈正弦变化的趋势。通过处理电路对接收线圈中感应交流电的幅值大小，就可以得到谐振器在天线板上方移动的相对位置，仿真结果与理论分析保持一致。

3结束语

本文分析研究了一种新型的高频、非接触式电磁感应式位移传感器，对传感器电磁耦合系统建模后，利用毕奥-萨伐尔定律推导激励天线在空间点电磁场分布表达式。利用Matlab仿真绘制系统空间区域电磁场分布情况，再从法拉第电磁感应定律出发，推导出感应天线中电流理论表达式。从理论计算上验证系统传感器工作原理的正确可靠性，再运用Ansoft Maxwell三维电磁仿真软件对系统的瞬态电磁场进行仿真分析与结构参数的确定。研究结果表明：

①当没有无源谐振器时，只考虑激励线圈对感应线圈中的感应电流的影响。由于感应电流只有0.4 mA，因此可以忽略激励线圈对感应线圈的直接影响。

②当谐振器位于天线板上方，由于激励交流电涡流效应，在谐振器和感应线圈中同时产生与激励交流电同频的感应电流。当谐振器线圈横向移动时，感应电流呈正弦变化趋势。

③谐振器距离天线板高度与感应线圈中产生的感

应电流大小成反比，考虑到装配尺寸可靠性以及感应电流易于检测，可以定谐振器距天线板2～3 mm。

④综合材料磁效应以及涡流效应，采用铜或铝作为天线材料比较合适，感应电流也易于检测。

参考文献

[1] 图尔克(天津)传感器有限公司.一个新时代电感谐振电路技术开创了位置检测的新时代输水调度集中监控系统应用[J].国内外机电一体化技术,2011(4):45-46.

[2] Rahal M,Demosthenous A.An integrated signal conditioner for high-frequency inductive position sensors[J].Measurement Science and Technology,2010,21(1):015203.

[3] AndrewNicholas D,DavidThomasEliot E,AndrewRobert H.Position encoder:European Patent ,PatentEP19950918680[P].1995-03-15.http://www.freepatentsonline.com/EP0760087B9.html.

[4] Byrne J V,McMullin F,Murray A.Position and speed sensors: U.S.Patent 4,737,698[P].1988-04-12.http://www.freepatentsonline.com/4737698.html.

[5] 图尔克(天津)传感器有限公司.电感式直线位移传感器在机床行业的应用[J].国内外机电一体化技术,2011(1):42-43.

[6] 李钟泽.关于计算机感应电动势的三个公式[J].洛阳大学学报,1995(2):86-89.

[7] 葛松华.通以交变电流的长直螺线管内部磁场和电场的分布[J].物理与工程,2003,13(6)：6-8.

[8] 张晓燕,季学武.电磁感应式转向盘转速传感器的研究[J].仪器仪表学报,2009,30(12):2551-2556.

[9] 李凌,杨明,叶林.感应式非接触角度传感器电磁耦合系统设计[J].传感器与微系统,2011,30(10):130-132.

Research on the Design of Coupling Antenna for Electromagnetic Induction Displacement Sensor

丁莹1,2董全林1,2刘会森1,2张玉莲3张春熹1,2

(微纳测控与低维物理教育部重点实验室1,北京100191；

北京航空航天大学仪器科学与光电工程学院2,北京100191；河南教育学院3，河南 信阳450046)

摘要：新型电磁感应位移传感器具有非接触、无磨损、鲁棒性好等优势，广泛适用于各种行程与定位系统。收发天线与无源谐振器的电磁耦合特性直接影响着传感器位置测量精度。对天线电磁耦合系统工作原理和基本结构进行了研究，根据电磁场理论推导天线耦合系统电磁场分布表达式，用Matlab仿真验证模型设计的合理性与正确性。应用Ansoft Maxwell软件进行电磁性能仿真以及关键参数分析，给出合理的传感元件结构参数，为传感器的天线设计提供理论基础。

关键词：电磁感应电磁耦合电磁场天线传感器LC谐振器行程与定位系统

Abstract：New type of electromagnetic induction displacement sensors are widely used in stroke and positioning system because of their advantages of contactless, no wear and good robustness. The electromagnetic coupling characteristics of transmitting and receiving antennas and passive resonator directly affect the measurement accuracy of sensor. The operation principle and basic structure of antenna electromagnetic coupling system are studied, according to the theory of electromagnetic field, electromagnetic field distribution expression of antenna coupling system is derived, and the rationality and correctness of model design is verified through Matlab simulation. Meanwhile, Ansoft Maxwell software is applied to simulate the electromagnetic performance and analyze the crucial parameters, then the reasonable structure parameters of sensing element are given, which provides a theoretical basis for designing aerial system of the sensor.

Keywords:Electromagnetic inductionElectromagnetic couplingElectromagnetic fieldAntennaSensorLC resonatorStroke and positioning system

中图分类号：TH711;TP273

文献标志码：A

DOI:10.16086/j.cnki.issn1000-0380.201604005

国家科技支撑计划基金资助项目(编号：2006BAK03A24)。

修改稿收到日期：2015-08-16。

第一作者丁莹(1991-)，女，现为北京航空航天大学光电工程专业在读硕士研究生；主要从事电磁感应式位移传感器、超显微仪器技术、惯性导航与制导方向的研究。