放缩法在数列不等式证明中的应用



放缩法在数列不等式证明中的应用

◇山东孙梅彦

在高考中,对数列求和的考查多种多样,其中证明与数列求和有关的不等式问题是高考热点与难点,解此类问题常用到“放缩法”．明析放缩法的技巧,对于同学们熟练解决此类问题大有裨益.下面就常用的放缩方法举例分析.

1裂项放缩

(1) 求a2的值;

(2) 求数列{an}的通项公式;

(3) 证明:对一切正整数n,有

(3) 证明: 由(2)知,an=n2,n∈N*.

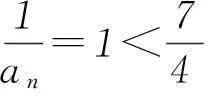
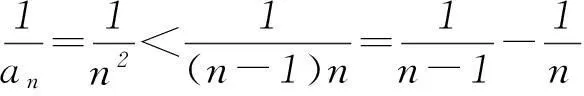
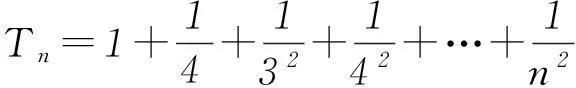
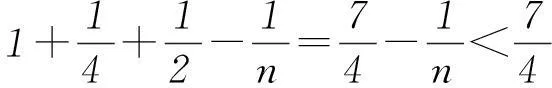
综上,对一切正整数n,有

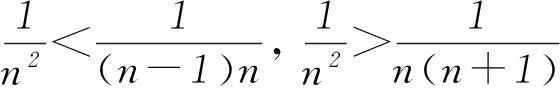
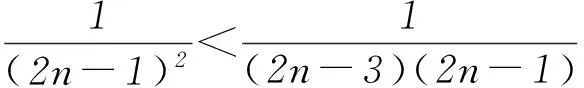
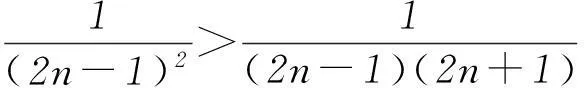
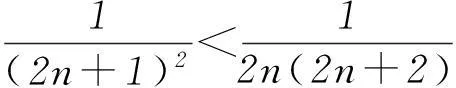
(k>1,k∈N*)等.

2累乘放缩

(1) 求数列{xn}的通项公式;

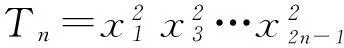
(2) 证明: 由题设和(1)中的计算结果知

当n=1时,T1=1/4.

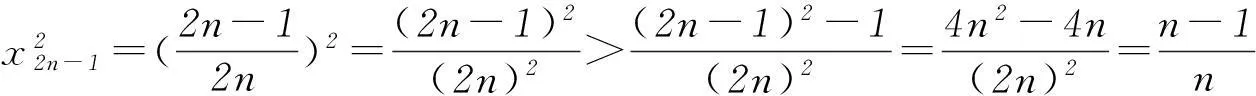
综上可得对任意的n∈N*,均有Tn≥1/4n.

3利用均值不等式

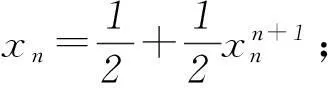
(2) 设有一个与上述等比数列的首项、末项、项数分别相同的等差数列,其各项和为gn(x),比较fn(x)与gn(x)的大小,并加以证明.

(2) 由题意,设{an}、{bn}分别是满足条件的等差和等比数列,{an}的公差为d,则an=1+(n-1)d,bn=xn-1且xn=1+nd,即d=(xn-1)/n．

若x=1,则an=bn,所以fn(x)=gn(x);

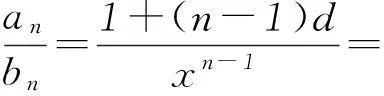
即bn

综上所述, 当x=1时,fn(x)=gn(x);当x>0且x≠1时,fn(x)

以上是数列与不等式综合题型中的常规放缩技巧,由于放缩法是一种非等价转化,放缩没有确定的准则和程序,放缩目的性很强,需按题意适当放缩.本文只是从部分角度来探究放缩法的一些技巧.

(作者单位：山东省乳山市第一中学)