谈立体几何综合题的解题策略
谈立体几何综合题的解题策略
◇北京孙世林童嘉森(特级教师)
谈到立体几何综合题的解法,首先想到的是空间向量,向量法解决立体几何问题思路简洁、操作容易,很好地避开对空间想象能力要求较高的几何推理,越来越受到师生的青睐.向量法逐步成为当前高考应考的“主流”方法.然而我们发现,向量的引入并未使立体几何的学习变得容易,普遍存在对向量知识理解不到位、不能把握向量解题的关键、计算不过关等现象.下面通过对2015年的几个高考题的分析谈谈立体几何综合题的解题策略.
1恰当建系准确计算,巧用坐标形式的向量
向量具有“数”与“形”双重身份,兼具代数的严谨与几何的直观,用坐标形式向量解决立体几何问题,因其思路简单、程序明确、操作容易成为师生的首选.运用坐标形式向量解题,就是将空间点、线、面的位置关系及角、距离等问题转化为向量问题,从而实现“形”向“数”的转化,最后通过向量的运算解决问题.

图1

(1) 证明:平面AEC⊥平面AFC.
(2) 求直线AE与CF所成角的余弦值.

图2

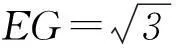
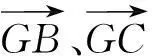
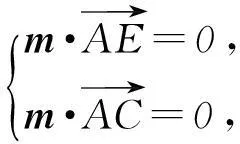
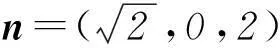

2回归向量知识本质,用非坐标形式向量
在解题中为避免难度较大的几何推理,同学们常建立空间坐标系利用坐标形式的向量解决问题,但试题中往往没有明确的垂直关系,建立坐标系要通过一定的转化、证明,计算难度较大,一味强调坐标法会造成得分的困难.出现这种现象一是空间想象能力、几何推理有待提高,再有就是对向量知识本质认识不够.恰当利用非坐标形式的向量解题,既可避开技巧要求过高、转化复杂的几何法,又可以很好的回避有时建系的困难.
下面继续探究例1.

所以
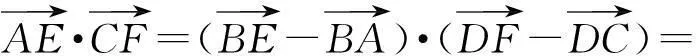
.
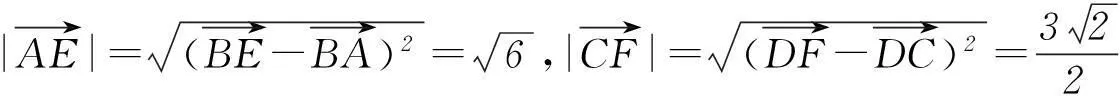




图3

(1) 证明:CD⊥平面A1OC;
(2) 若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角的余弦值.
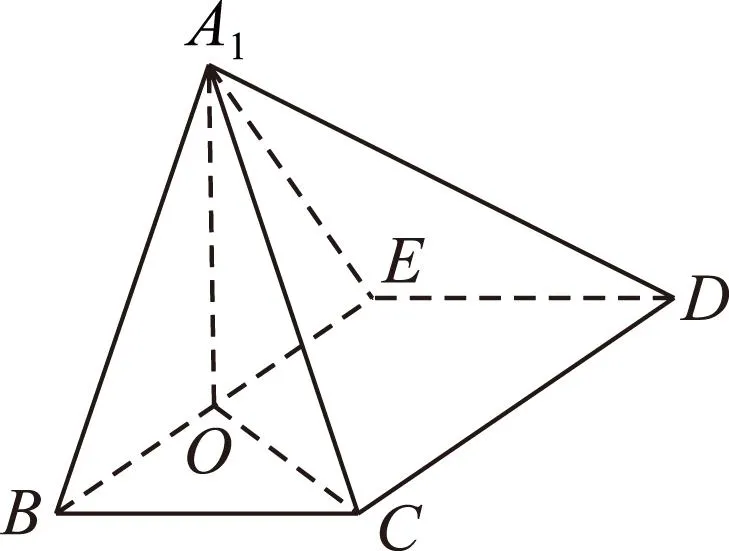
图4




图5

(1) 求平面PAB与平面PCD所成二面角的余弦值;
(2) 点Q是线段BP上的动点,当直线CQ与DP所成角最小时,求线段BQ的长.



由已知可证AP、AD、AB两两垂直,所以
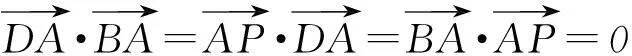
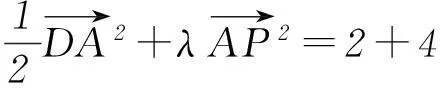
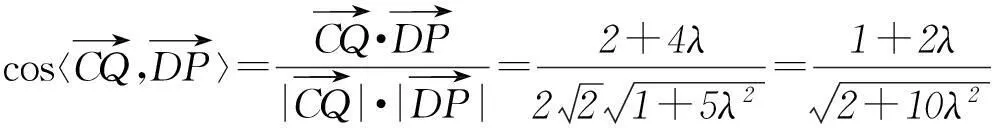
令1+2λ=t,t∈[1,3],所以
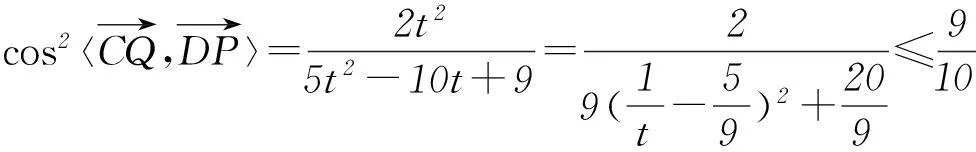
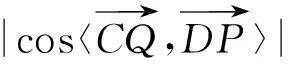
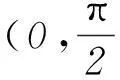

3不要过度依赖向量法,注重不同方法结合
向量法功能强大,但也不是什么样的题目用向量法都好,在证明线、面的平行与垂直问题时向量法有时显得有些烦琐,反而传统方法(即几何法)寥寥数语便可搞定,所以解题时要适时地选择坐标形式或非坐标形式,同时结合传统的几何法解决问题,从而方便快捷地解决立体几何问题.
我们再来看例1的第(1)问.

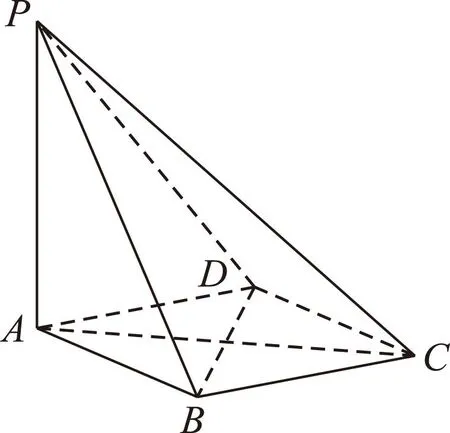
图6

(1) 求证:BD⊥平面PAC;
(2) 若PA=AB,求PB与AC所成角的余弦值;
(3) 当平面PBC与PDC垂直时,求PA的长.

4+2×2×cos 60°+0+0=6.
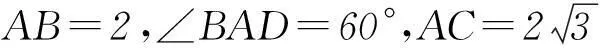
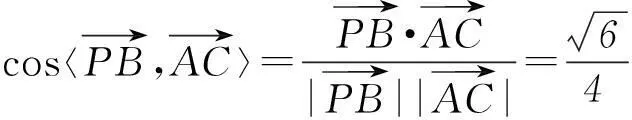
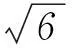
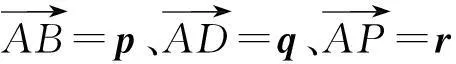
设平面PBC的法向量为m=p+xq+yr,所以

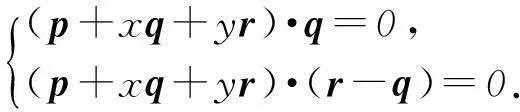
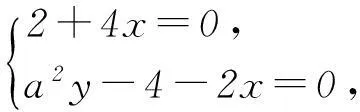
所以
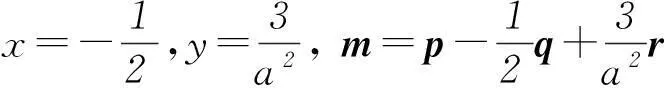
因为平面PBC⊥平面PDC,所以m与平面PDC是共面向量,所以存在实数λ1、λ2使
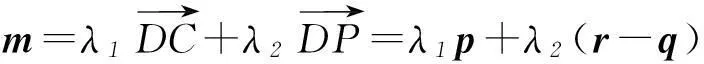
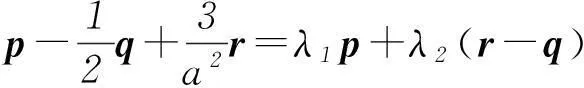

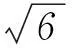

向量作为一种数学工具,它既可以进行代数运算又具有几何推理的功能.利用向量的几何意义,选择好坐标形式或非坐标形式的向量可以很方便地解决立体几何中很多问题.然而,向量法虽强,但它并不是万能的,我们要根据题目的条件和特点恰当应用传统的几何法,以完善立体几何思维,形成恰当的解题思路.

