借助导函数与原函数图象的关系巧解题



借助导函数与原函数图象的关系巧解题

◇辽宁范琦亮

导数是求解函数问题的有力工具,利用导函数的正、负,可简洁判断原函数的增减,进而求函数的极值、最值等．其中判断导函数的正、负是问题求解的关系步骤,具体应用时可借助导函数与原函数的关系．下面举例说明．

1根据导数的几何意义分析原函数的图象

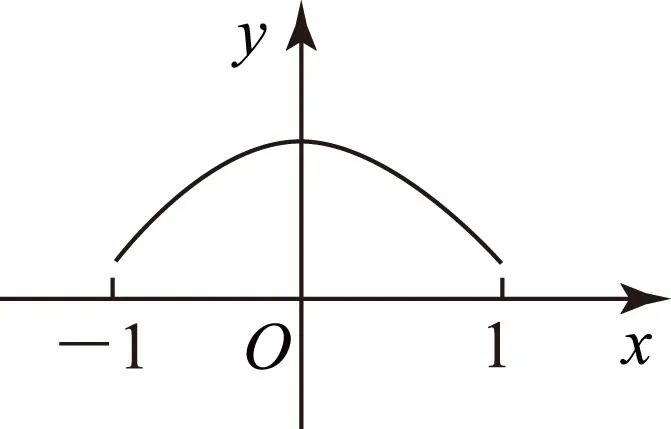
图1

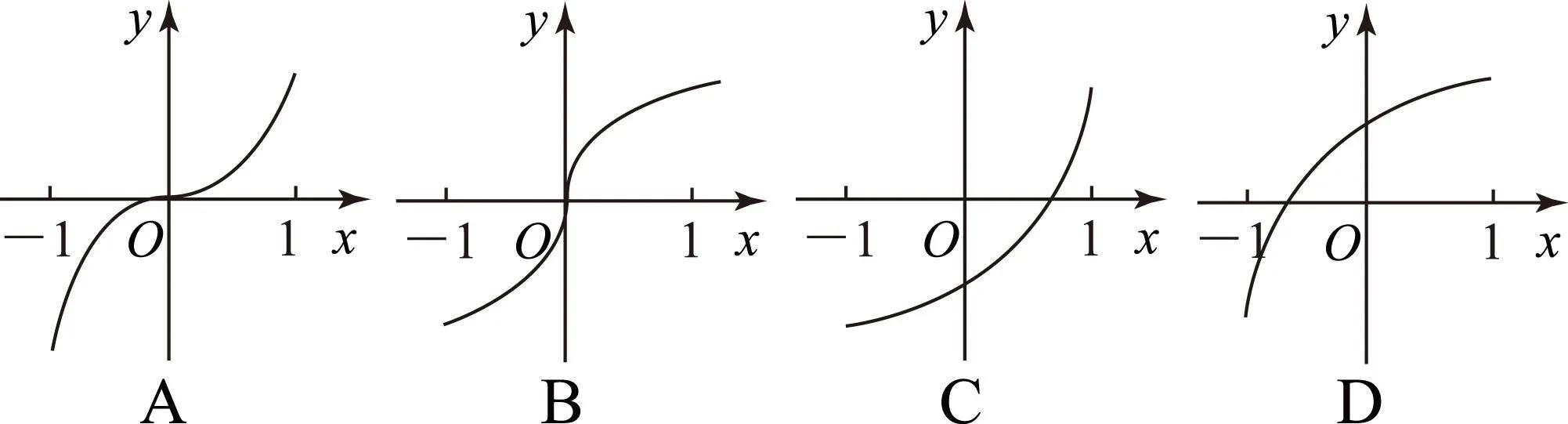
当x∈(-1,0)时,f′(x)单调递增,则f(x)图象的增长趋势由缓到快.当x∈(0,1)时f′(x)单调递减,则f(x)的图象增长趋势由快到缓,故选B.

2根据函数的图象特征求解析式

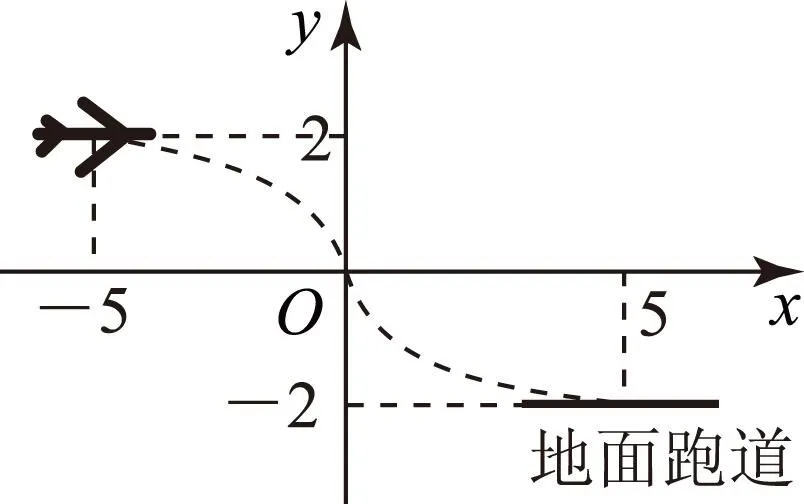
图2

A y=1125x3-35x; B y=2125x3-45x;

3根据函数与其导函数的图象关系巧解题

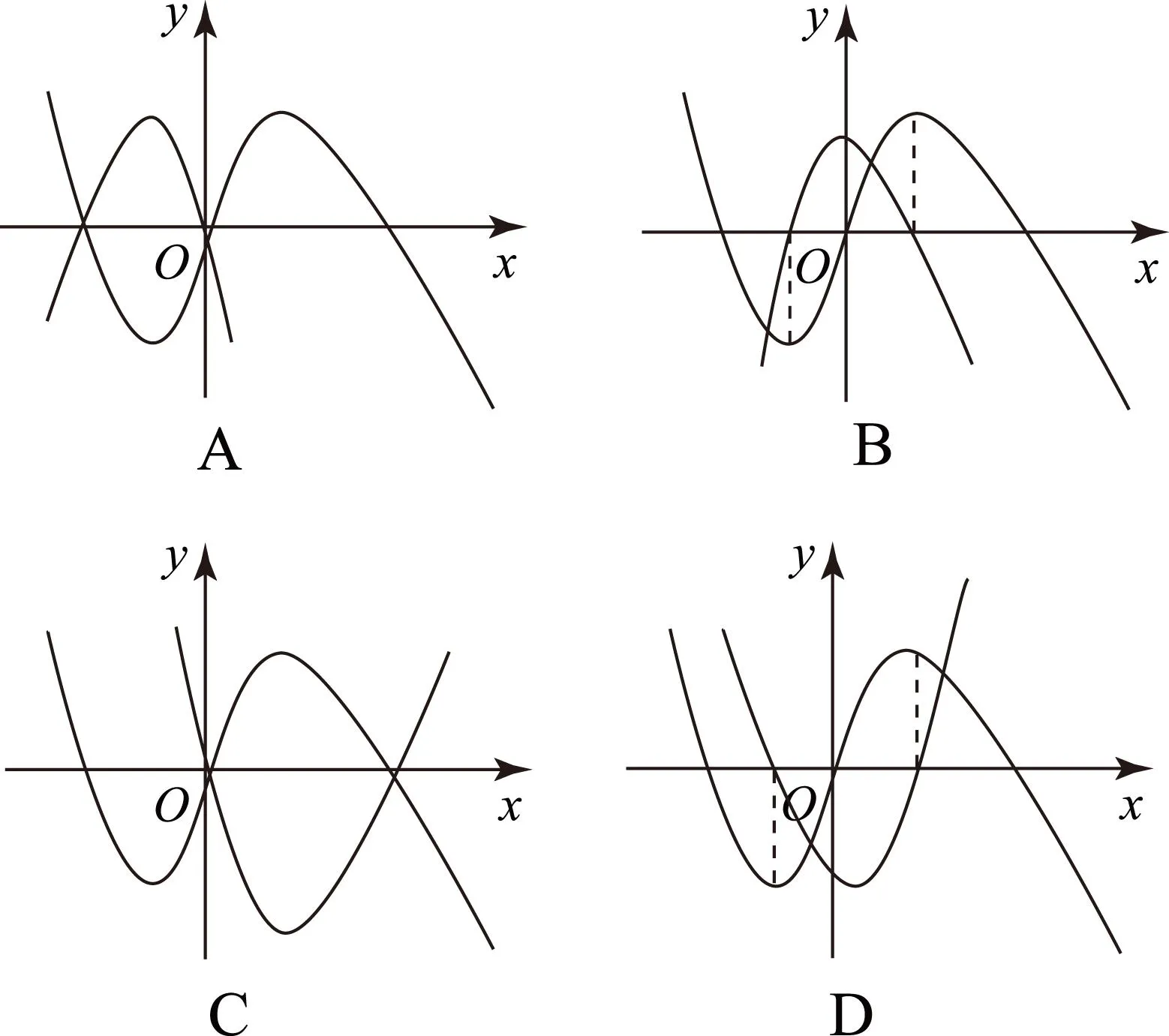
4由导函数图象分析原函数拐点和极值点

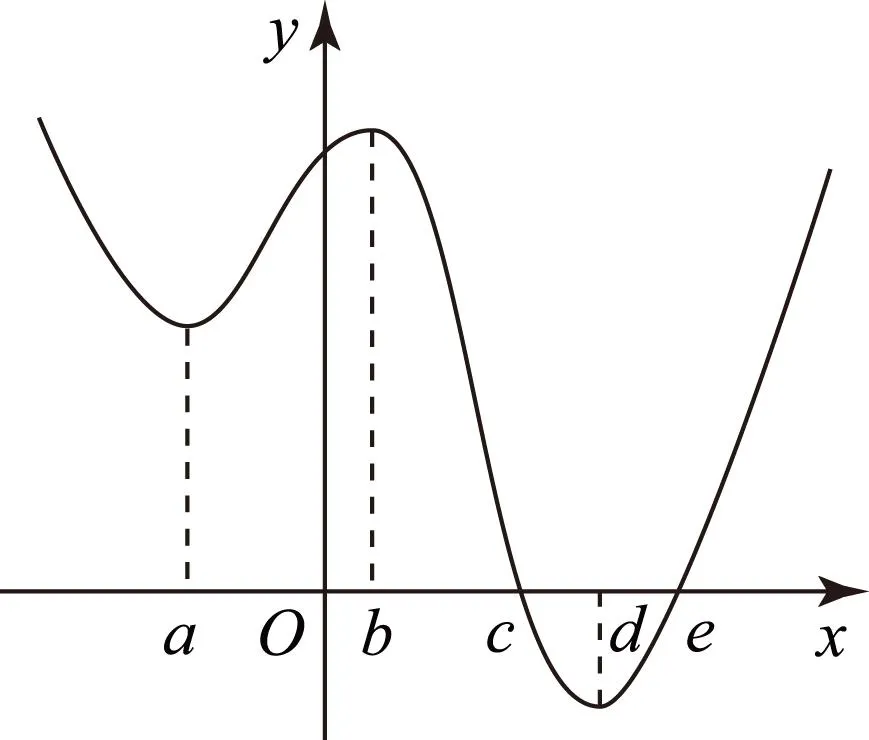
图3

Af(b)>f(c)>f(d);

Bf(b)>f(a)>f(e);

Cf(c)>f(b)>f(a);

Df(c)>f(e)>f(d)

又af(b)>f(a),选C.

5借助图象 简洁求原函数最值

(1) 求f(x)在点(0,f(0))处的切线方程.

(2) 求证:当x∈(0, 1)时,f(x)>2(x+x3/3).

(3) 设实数k使得f(x)>k(x+x3/3)对x∈(0, 1)恒成立,求k的最大值.

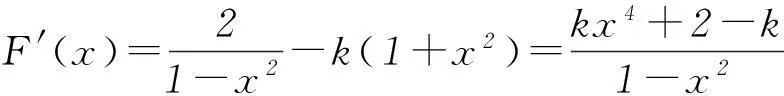
当k∈[0,2]时,F′(x)≥0,函数在(0,1)内为增函数,F(x)>F(0)=0,符合题意,此时k的最大值为2.

x(0,x0)x0(x0,1)F'(x)-0+F(x)↘极小值↗

所以在区间(0,1)内Fmin(x)=F(x0)．

解题至此,部分同学欲求F(x0),陷入误区．此时可借助图象,转换方向去求F(0),而F(0)=0,故F(x0)<0,所以F(x)>0不成立．

综上所述,可知k的最大值为2.

综上,求解导函数与原函数图象的交会问题,其关键在于熟练掌握导数这一有力工具,以“数形结合法”的方式去分析、解决问题.

(作者单位：辽宁省普兰店市大连海湾高级中学)