例谈处理“外接球”问题的常用策略
2016-04-28 02:10赵加勇
高中数理化 2016年2期
例谈处理“外接球”问题的常用策略
◇山东赵加勇
在立体几何试题中,我们经常会遇到这样一类问题:“由题设条件,计算某几何体的外接球的表面积或体积.”因为S球=4πR2,V球=4πR3/3,所以关键是计算外接球的半径R.那么,如何计算外接球的半径呢?下面归类解析.
1构造特殊几何体


图1


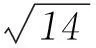


2利用直角三角形的边角关系


图2


3借助直角三角形斜边中线的性质


图3

又AC∩CD=C,所以AB⊥平面ACD,所以AB⊥AD.设线段BD的中点为O,则点O既是Rt△ABD斜边的中点,也是Rt△BCD斜边的中点.于是,由直角三角形的特性即知点O到A、B、C、D4个顶点的距离相等.从而,该三棱锥外接球的球心为O,半径为
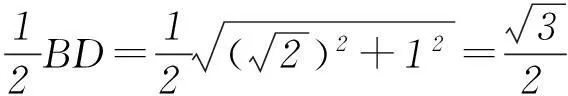


4借助底面三角形的外接圆



综上,处理此类“外接球”问题时,需要灵活运用有关平面图形或立体图形的特性去分析球心的位置,并计算球的半径.
(作者单位:山东省阳谷县第三中学)
猜你喜欢
中学生数理化(高中版.高考数学)(2022年2期)2022-04-26
中学数学教学(2019年3期)2019-06-21
福建中学数学(2018年1期)2018-11-29
中等数学(2018年8期)2018-11-10
中学生数理化(高中版.高二数学)(2018年1期)2018-02-26
中学数学杂志(高中版)(2018年1期)2018-01-27
教学考试(高考数学)(2017年2期)2017-08-11
福建中学数学(2016年4期)2016-10-19
中学教学参考·理科版(2014年3期)2014-04-10
中学数学杂志(高中版)(2008年4期)2008-07-31

