探讨函数单调性的判定方法
探讨函数单调性的判定方法
◇江苏鲍怡
单调性是函数的重要性质之一,在高考中以单调性为背景的问题屡见不鲜,解题的关键是先判断出函数的单调性,再应用其解题.本文从如下几个方面对单调性进行探讨.
1函数单调性定义
设定函数y=f(x) 的定义域为A,区间I⊆A.如果区间I内的任意2个自变量x1、x2,当x1
注: 函数的单调性是在定义域内某个区间上的性质,是函数的局部性质.所以在对函数的单调性进行研究时,首先要明确所属区间.
2函数单调性的判断方法
2.1定义法
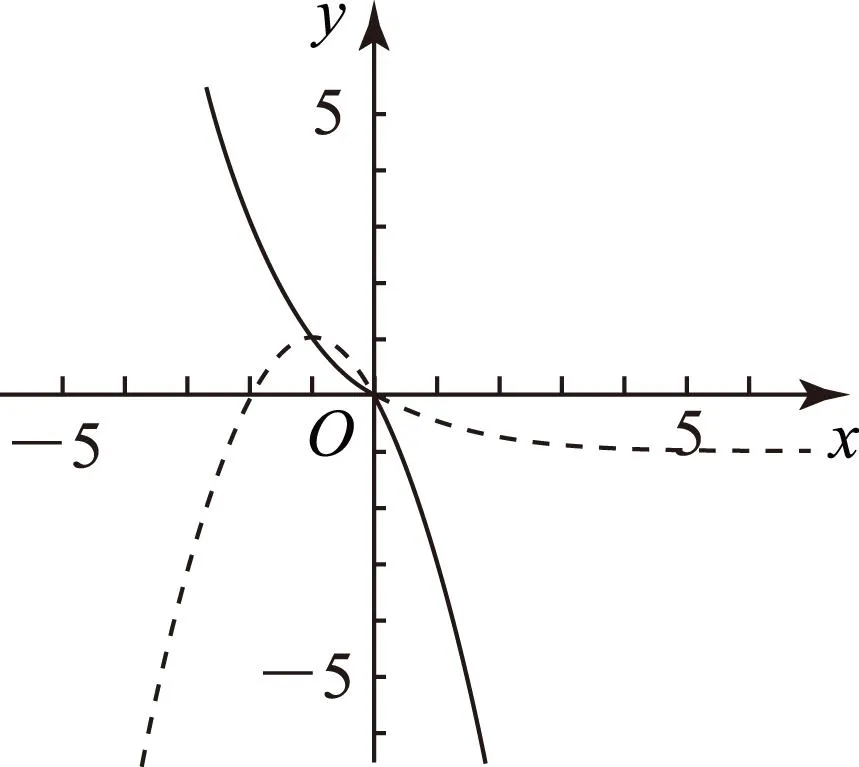
利用定义判断函数单调性时,可分3个步骤:1)求出函数的定义域; 2)在定义域内任意设定2个值x1 所以f(x1)>f(x2).因此,函数f(x)在区间(0,+∞)内为单调减函数.同理f(x)在区间(-∞,0)内为单调减函数. 2.2组合函数法 如函数f(x)、g(x)均为区间A内的增函数,则f(x)+g(x)也是区间A内的增函数;若f(x)为区间A内的增函数,g(x)为区间A内的减函数,则f(x)-g(x)为 区间A内的增函数,g(x)-f(x)为区间A内的减函数. 2.3图象法 根据函数图象进行函数单调性的判断.具体来讲,就是在单调区间内,如果函数图象一直呈上升状态,函数就为单调增函数.而函数图象一直呈下降趋势,则函数为单调减函数. 图1 2.4复合函数法 在高中数学教材中,复合函数定义:函数y=f(g(x))是由函数y=f(t)和t=g(x)组合而成的,其中t=g(x)为内层函数,y=f(t)为外层函数.根据复合函数的单调性定义,在内、外层函数单调性不同的情况下,复合函数为单调减函数;在内、外层函数单调性相同时,复合函数为单调增函数. 对于较复杂的函数还可利用导数法来判断其单调性.总之,学会判断函数的单调性是学好函数的基础.在高考中出现的频率也非常高,只要灵活运用图象法、定义法、复合函数法、导数法等即可顺利解题. (作者单位:江苏省苏州市第一中学)