波翼相位差对柔性翼水动力性能的影响
刘鹏, 苏玉民, 李宁宇
(1.中国海洋大学 工程学院,山东 青岛 266100;2.哈尔滨工程大学 水下机器人技术重点实验室,黑龙江 哈尔滨 150001)
波翼相位差对柔性翼水动力性能的影响
刘鹏1,2, 苏玉民2, 李宁宇2
(1.中国海洋大学 工程学院,山东 青岛 266100;2.哈尔滨工程大学 水下机器人技术重点实验室,黑龙江 哈尔滨 150001)
摘要:以仿生推进系统利用波浪能为背景,研究了波翼相位差对规则波下近波面二维柔性拍动翼的推进性能的影响。采用求解RANS方程的方法,计算了不同波翼相位差下柔性翼的水动力性能,并与无波情况下及相同工况下刚性翼结果进行比较。计算结果显示:波翼相位差对翼水动力系数的相位、幅值有影响,恰当波翼相位差下,柔性翼能有效利用波浪能增加自身推力及效率,且其对波浪能的利用能力高于刚性翼。尾涡分析表明,恰当的波翼相位差能够提高柔性翼尾涡梯度及其连续性,从而提高波面下柔性翼推力及效率。
关键词:柔性翼;规则波;波翼相位差;水动力性能;尾涡
微小型水下机器人以其体积小、机动灵活、隐身性强等特点成为目前研究的热点,而采用性能优良的推进装置则是这些特点的重要保障[1]。
鱼类经过长期的自然选择与进化拥有了非凡的水中游动能力,采用仿鱼类摆动鳍推进的仿生水下机器人以其高效率、低噪声及高机动性引起了各国学者的广泛关注。1994年,麻省理工学院模仿金枪鱼制造了RoboTuna[2],开始研究鱼类高效游动的机理。Jones等[3-5]采用面元法计算了二维拍动翼的推进性能,并进行了相应的实验研究。刘鹏飞[6]采用三维面元法探讨了不同运动参数对摆式推进器推力和效率的影响。于宪钊等[7]采用计算流体力学方法分析了对拍翼推进器的性能情况。张曦等分析了半圆柱后拍动翼及非对称运动翼的水动力性能[8]。刘鹏等[9-10]研究了串列翼脉动情况下的水动力性能。苏玉民等[11-12]探讨了柔性变形对翼性能的影响。
以上研究均假定翼处于无界流体中,而在实际应用时,许多情况下要求仿生水下机器人近水面长时间运行,此时海洋波浪将会对翼的性能产生巨大影响。此外,常规仿生推进装置以燃油或电池作为动力源,导致其续航力低且极易造成海洋环境污染,而波浪能是海洋中蕴量丰富的一种能量形式,因此研究拍动翼在近波面运动时如何减小波浪不利影响甚至有效利用波浪能推进,对提高仿生水下机器人航行性能、减少海洋环境污染等均具有重要的意义[13]。Wu[14]首先提出水翼近波面运动时可从周围流体中获取能量的理论。Isshiki等[15-16]根据Wu的理论提出以近波面自由摇荡水翼作为推进器的设想并完成了相应试验。对于受迫运动拍动翼,Yamaguchi等[17]采用有限体积法计算了近波面水翼不同环境参数下的推力情况。
近波面运动时,水翼遭遇波浪的状态不同将会导致其运动与波浪水质点运动间存在相位差,这一相位差称为波翼相位差。文献[14,17]指出其对水翼的推进性能具有极为重要的影响,但其研究中尚缺乏对翼流场的分析;另外研究表明柔性翼相比刚性翼能够更有效的产生推力[18-19],也更贴近鱼类尾鳍运动形式,而已有研究中对象均为刚性水翼。
本文通过计算流体动力学方法计算了不同波翼相位差下柔性翼的水动力性能,采用CFD软件Fluent分析了波翼相位差对柔性翼水动力性能的影响,并同无波情况下及相同工况下刚性翼性能进行了比较。结果表明了波面下柔性翼良好的推进性能及其利用波浪能推进的可行性。
1数值计算的基本原理和方法
1.1数值计算模型
如图1所示,沉深hl、弦长c的水翼在水深hw的二维数值水池中做升沉幅度h0、摆幅角θ0的拍动运动,来流速度U、入射规则波波长λ、波高h=2a。大地坐标系原点位于水入口与空气入口相交点处,波传播方向沿x轴正方向,y轴以指向空气域为正。翼随体坐标系x=0点位于翼纵摇中心。
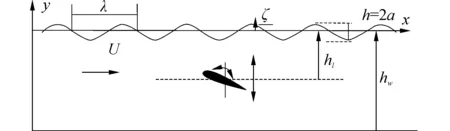
图1 近波面拍动翼坐标系Fig. 1 Body coordinate system for an oscillating hydrofoil under a wave
线性规则波波形方程为
(1)
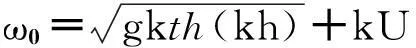
翼运动规律人为给出,分别做以其前缘点为转动中心的摇摆运动和沿y轴的升沉运动,均满足正弦规律[20]:
(2)
(3)
式中:f为水翼自身运动频率,ψ为波翼相位差,φ为水翼纵摇与升沉运动间的相位差。
柔性翼沿弦长方向变形,整个翼柔性变形的变形规律表示为[12]
(4)
式中:δc为变形运动的振幅;f为变形运动的频率,该频率和水翼摇摆、升沉的频率相等;s、ε为变形运动的控制参数,其中s、ε>1,s越大变形越靠近翼首缘,ε越大变形越靠近翼尾缘。φ0为柔性变形与升沉运动的相位角。
对瞬时沿-x方向翼推力Fx、y方向的升力Fy、绕翼前缘点的力矩M进行无因次化得到推力系数Ct、侧向力系数Cy、力矩系数Cm[21]定义如下
(5)
式中:ρ为水的密度。t时刻输入功率P:
(6)
可得t时刻输入功率系数Cp与输出功率系数Cpo[22]:
(7)
水翼运动的自身推进效率η[23]:
(8)
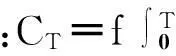
(9)
式中:Cg为波的群速度,定义水翼回收波浪功率系数Cpr=Cpow-Cpon,其中Cpow为近波面水翼的输出功率系数,Cpon为近静水面时水翼的输出功率系数。于是可得近波面水翼对波浪能的回收效率ηr=Cpr/Cpw。
1.2数值计算方法
文中采用RNGk-ε模型求解RANS方程,在二维笛卡尔坐标系下,以张量形式表示的时均连续性方程和RANS方程可写为[24]
(10)
(11)
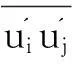
采用速度边界造波和阻尼消波法形成二维数值水池,采用VOF方法捕捉自由液面变化[25-26]。根据式(2)、(3),应用用户自定义函数(UDF)在Fluent中设定翼的运动规律。边界条件设置与计算域网格划分如图2、3所示,翼运动区域采用非结构网格划分,为保证计算精度,在自由液面及翼附近对网格进行加密[27]。采用动网格技术保证水翼运动过程中的网格质量。
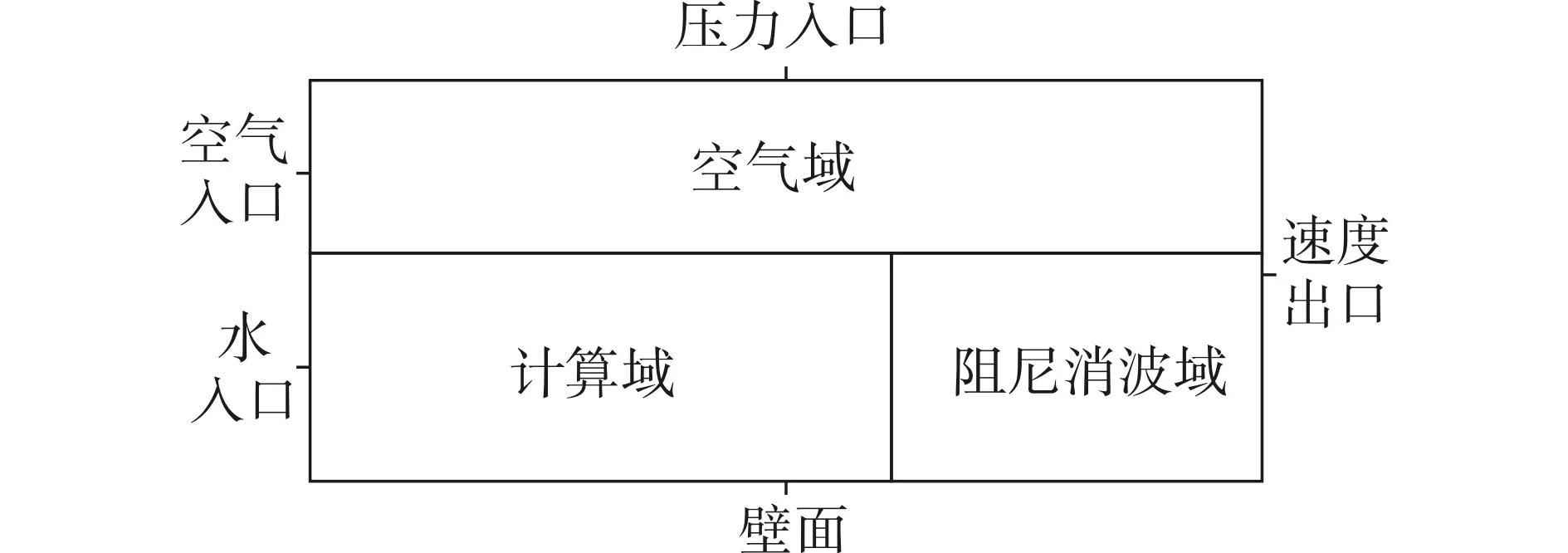
图2 数值水池示意图Fig. 2 Schematic diagram of numerical wave tank
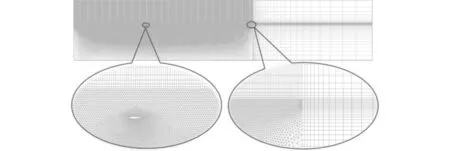
图3 计算域网格Fig. 3 Schematic diagram of mesh systems
2数值计算方法有效性验证
Isshiki于1984年完成了处于波面下自由运动水翼推进性能的试验研究,试验水池尺度为25 m×1 m×0.71 m,试验水翼翼型为弦长c=0.4 m的NACA0015翼型,翼纵摇中心距前缘点0.12 m,规则波波幅a=0.048 m,翼其他运动参数如升沉幅度、摆幅角等的取值均与文献[16]中结果相同。计算中取翼运动频率等于波浪遭遇频率。
基于求解RANS方程方法所得计算结果与试验值及Wu[14]、Yamaguchi[17]、Grue[24]的计算结果比较如图4所示。图中k为波数,c为翼弦长。从图4中曲线趋势可知,在kc值较小时,4种数值计算方法均与试验值可较好的吻合,而当kc>1.2时,只有本文与Yamaguchi[17]的计算结果与试验值贴合更好,可以表明文中所采用的数值计算方法对所研究问题的有效性。
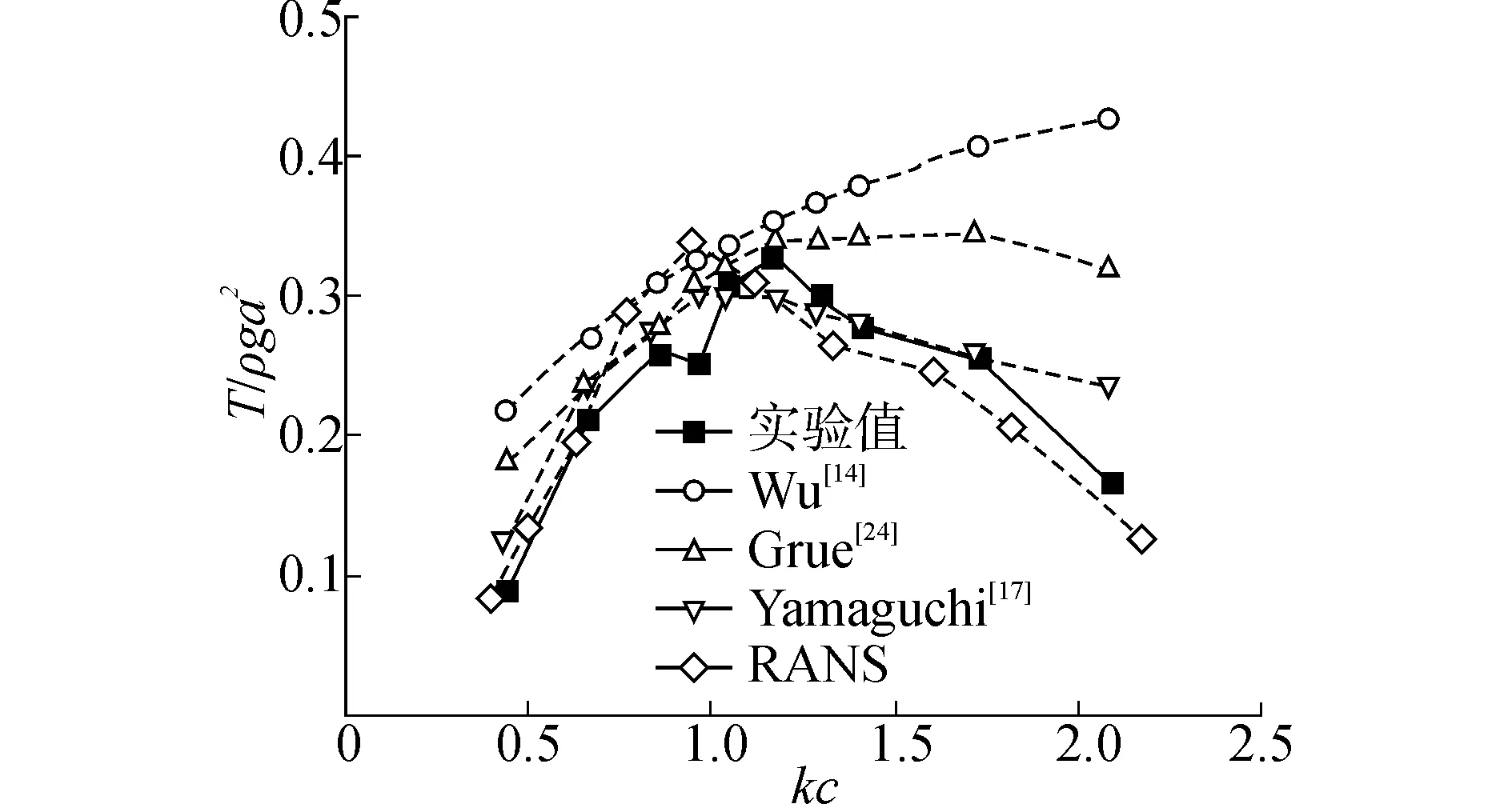
图4 不同kc下无因次推力值比较Fig. 4 Comparison of non-dimensional thrust between experiment and theory
3数值计算结果与分析
本文对柔性运动水翼在不同波翼相位差ψ下的水动力性能进行了计算。计算参数设置为:数值水池长L=25 m,水深hw=3 m,空气域高ha=2 m,沿x方向均匀流速u=0.1 m/s,波高h=2a=0.04 m,波长λ=6.64 m,翼型NACA0012,弦长c=0.1 m,沉深hl=0.1m,翼摇摆与升沉相位差φ=90°,翼周期T=2s= 1/f=2π/ωf,ωf为翼运动圆频率。柔性变形振幅δc=0.2c,φ0=-90°。柔性变形控制参数s=100、ε=2.0。翼运动升沉幅度h0=0.5c,摆幅角θ0=±15°,遭遇频率ω0= ωf。ψ取-180°~180°。文中同时计算了刚性翼在相同参数下的性能情况作为比较,同时还讨论ψ对尾涡的影响。
提高二级学院的财务管理水平 目前,二级学院的财务管理水平是制约二级财务普及的重要因素。各个高职院校要采取各种措施提升二级学院的财务管理水平,如设置专门的财务人员,或将二级学院相关的人员送出去培训。此外,要加强二级学院财务的内部审计,根据《中华人民共和国审计法》建立内部审计办法。这样一方面可以监控二级学院的财务管理,另一方面可以间接提升二级学院的财务管理水平,具有双重效果。
首先以刚性翼为例,给出ψ的定义。如图5所示,翼运动姿态及位置按时间先后分别如图中①~③所示。图中纵轴位于某一波峰处,定义若翼运动至②状态时遭遇波峰,则取ψ=0°,即为图5所示;若在①状态时遭遇波峰,则取ψ=-90°;若在③状态时遭遇波峰,则取ψ=90°,其他位置以此类推。
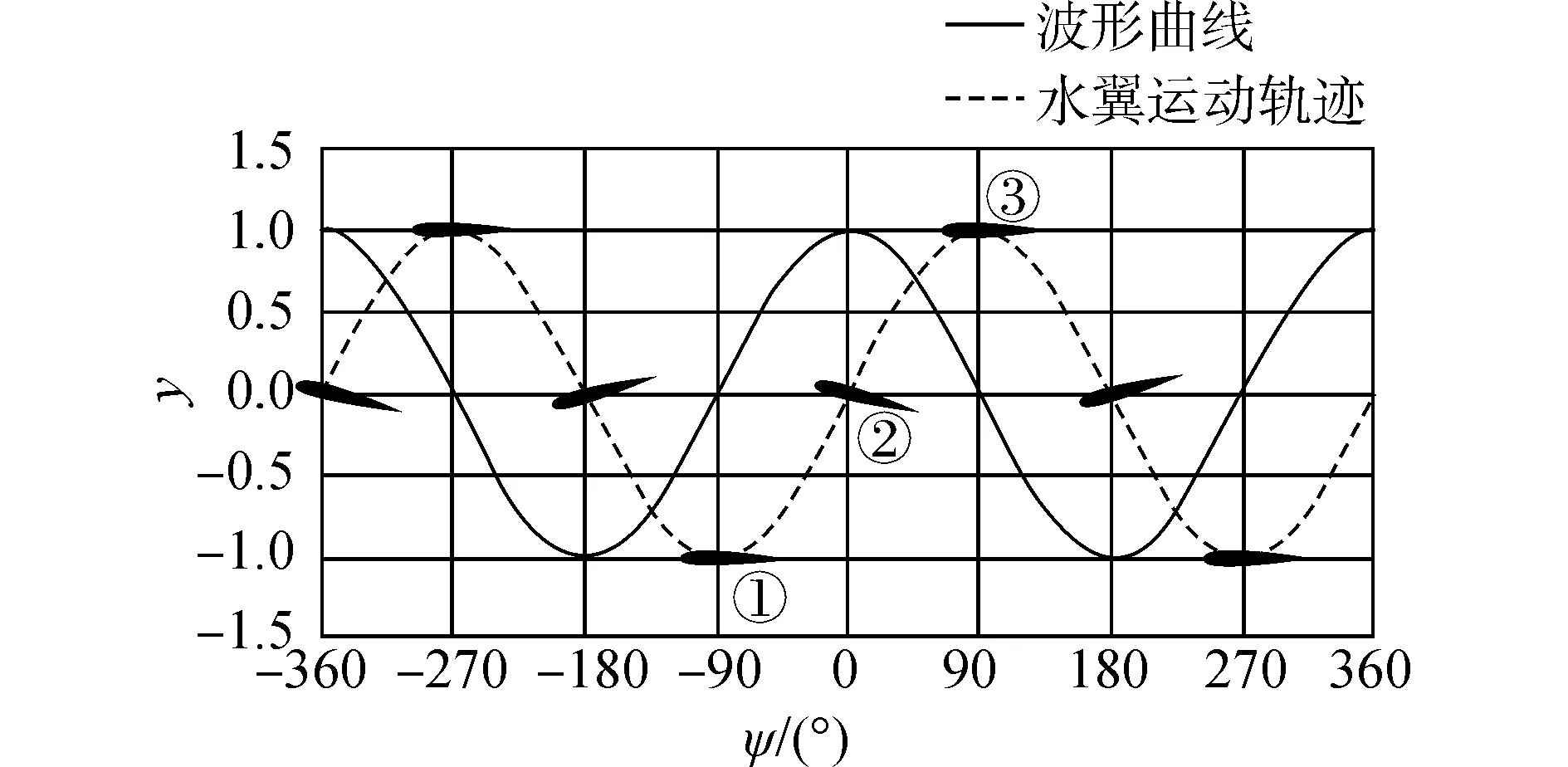
图5 波翼相位差示意图Fig. 5 Schematic diagram of wave phase difference
3.1波翼相位差对水动力系数的影响
柔性翼处于无波液面下及在ψ等于-90°、0°、90°时波面下相对应的推力系数Ct、侧向力系数Cy、力矩系数Cm如图6所示。图中同时给出了刚性翼在波面下ψ=-90°及无波水面下的力系数作为比较。图例中,F表示柔性翼,R表示刚性翼。
在不同的ψ下,推力系数Ct随时间的变化规律类似:在一个运动周期内,Ct随时间连续变化2次,以此在图6(a)中曲线存在2个波峰:一个出现在0-T/4,另一个出现在T/2以后。ψ对Ct的影响主要体现在相位和幅值两方面,对相位的影响表现在图6(a)中Ct峰值出现时间的早晚,从图中波面下柔性翼Ct曲线可知,ψ从-90°变化到90°时,Ct的峰值逐渐偏离T/2时刻;ψ对Ct幅值的影响主要表现在,一个周期内Ct最大值在ψ=0时最大,ψ=-90°时次之,ψ=90°时最小,此外,ψ=0时,Ct曲线的两个峰值差别最小。对比无波情况下的柔性翼Ct曲线可知,波面的存在同时影响了Ct的相位与幅值,合适的相位角能够有效提高翼的推力。比较柔性翼与刚性翼在不同情况下Ct曲线可知,柔性的存在能够使Ct的2个峰值差别减小而趋于相等。

图6 不同波翼相位差下的水动力系数比较Fig. 6 The comparison of hydrodynamic coefficients versus wave phase difference
由图6(b)可知,水翼在不同ψ下侧向力系数Cy随时间的变化规律为:在1个运动周期内Cy连续变化1次,分别存在1个波峰1个波谷,两者大小相等,方向相反。波谷出现时间在0~T/4之间,而波峰则出现在T/2左右。ψ对Cy相位的影响体现在随着ψ的增大,Cy峰谷出现的时刻逐渐滞后;ψ对Cy幅值的影响体现在ψ=0时Cy变化幅度最大,ψ=-90°时次之,ψ=90°时最小。翼柔性的存在主要减小了Cy曲线的波动幅度,而波面的存在则增大了Cy的幅值,二者对Cy的相位也有一定的影响。
由图6(c)可以看出,翼力矩系数Cm随ψ的变化同Cy的变化规律类似,但Cm的幅值要比Cy幅值小的多。
3.2波翼相位差对平均推力系数及波浪回收功率系数的影响
柔性翼与刚性翼在不同液面条件下平均推力系数CT与波浪回收功率Cpr随ψ的变化规律如图7所示。刚性翼与柔性翼的CT与Cpr均是随着ψ的增加呈近正弦规律变化。CT在ψ=-45°附近取得峰值,而在ψ=135°达到最小值,相比无波情况下翼CT值,在ψ=-45°时,由于波浪作用,柔性翼与刚性翼的推力系数分别可增加85.6%、74.4%,因此,处于波面下的运动翼在合适的ψ下可使自身推进力获得较大幅度的提升。同时,在ψ=-45°时,柔性翼的CT比刚性翼最高高出8.2%,且在不同ψ下,柔性翼的CT均不小于相同工况下刚性翼的推力系数,此外,无波情况下,柔性翼CT约高出刚性翼CT值1.7%。由Cpr曲线可知,ψ在-160°~45°,Cpr>0,表明恰当的ψ能够使刚性翼与柔性翼从波浪中吸收能量,而不当的ψ反而会使翼自身功率损失于周围波浪环境之中。同时,柔性翼对波浪能的利用能力要高于刚性翼。
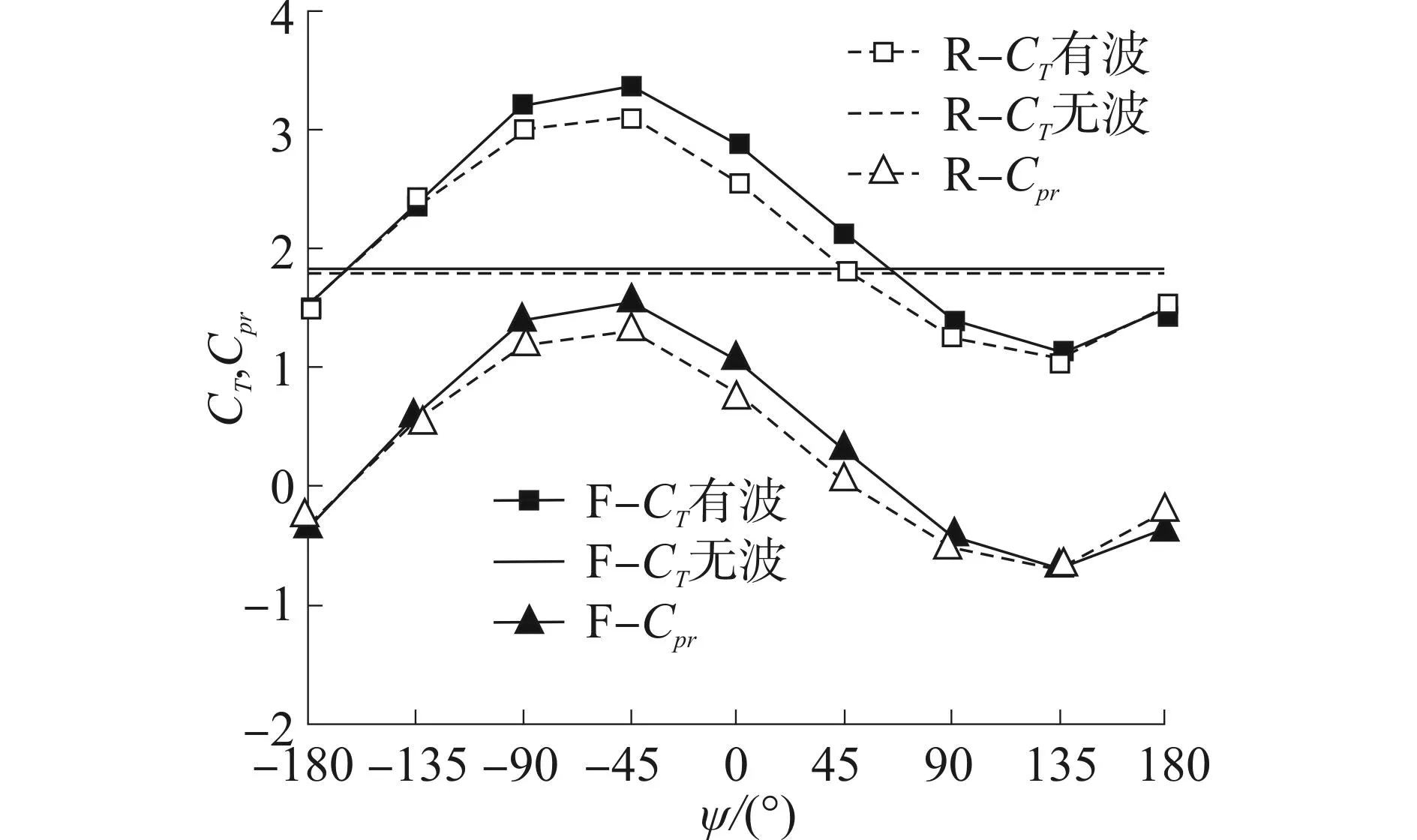
图7 不同波翼相位差下的CT与CprFig. 7 The mean thrust force coefficients and Wave energy recovered coefficients versus wave phase difference
3.3波翼相位差对推进效率及波浪能回收效率的影响
不同ψ下刚性翼与柔性翼推进效率η及波浪能利用效率ηr如图8所示。
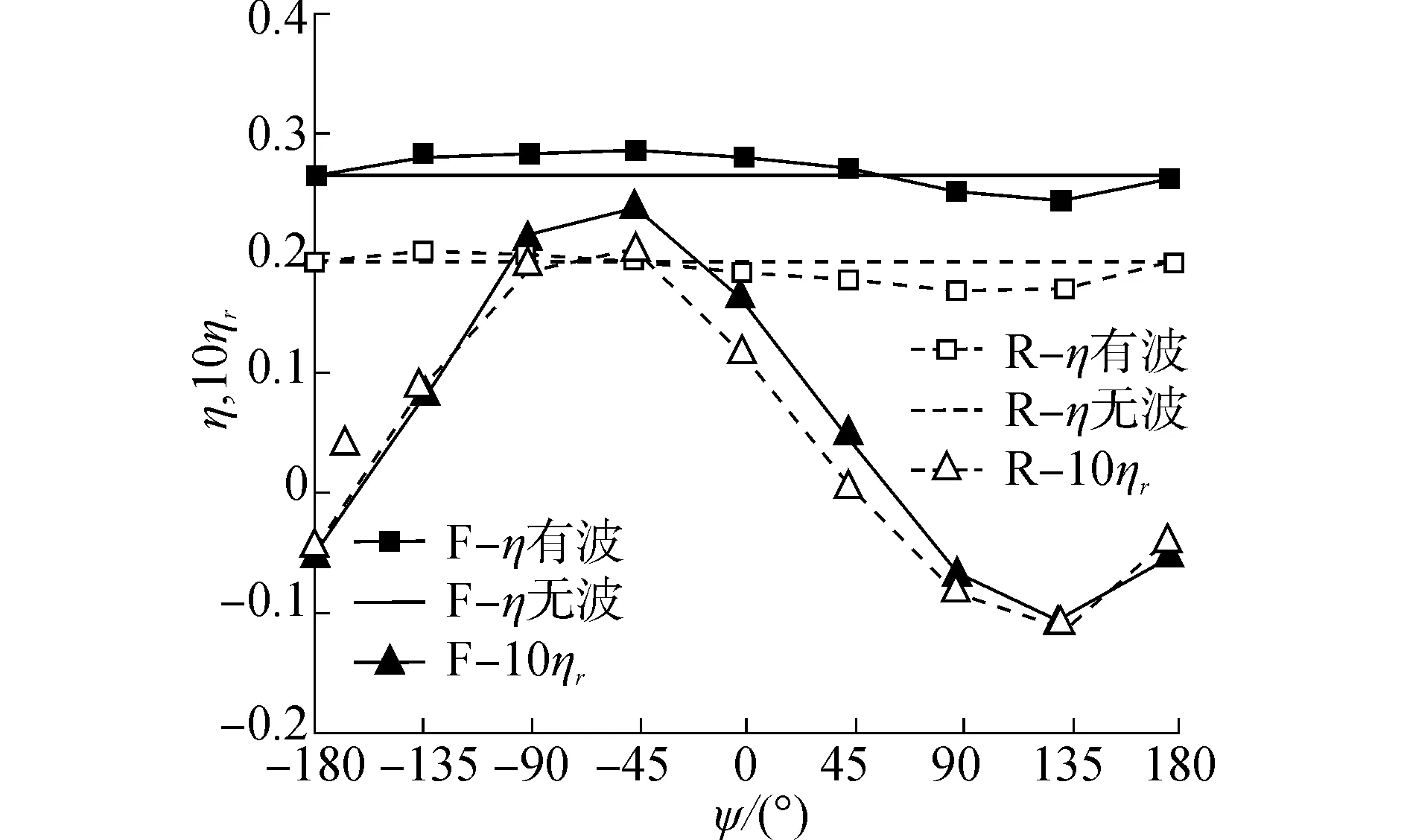
图8 效率随波翼相位差的变化Fig. 8 Wave energy recovered and propulsive coefficients versus wave phase difference
水翼近波面运动时,其η及ηr均是随着ψ的增加呈正弦趋势变化,峰值出现在ψ=-45°左右,谷值出现在ψ=135°左右。从η曲线趋势可以看出,在ψ选择得当情况下,水翼不仅能够获得高于无波情况下的推力值,又能获得高出无波情况下的推进效率,其中,在ψ=-45°时,波浪作用可使柔性翼效率提高7.2%,使刚性翼效率提高1.2%。此外任意ψ及无波情况下,柔性翼的推进效率均高于刚性翼效率,差别最大出现在ψ=0°,此时柔性翼η值高出刚性翼η值50.6%,无波情况下则高出36.6%。而由柔性翼ηr曲线可知,ηr在ψ处于-160°~45°时,均大于0,对应此时翼的推进效率高于其处于无波水面下情况;在ψ=-45°左右时,柔性翼与刚性翼的波浪能利用效率均达到最高,表明合适的波翼相位差下,水翼能够从波浪中获取能量,提高自身的推进效率,此外,柔性翼的波浪能利用效果多数情况下要高于刚性翼。
3.4波翼相位差对翼尾涡的影响
水翼通过摆动产生的漩涡呈反卡门涡街形式排列,使得水翼后方流体呈喷射状态[28-30],由于这部分流体的反作用,水翼受到前进的推力,因此尾涡对水翼推力具有极其重要的影响[31-32]。
柔性翼在不同ψ的波浪环境及无波环境下一个周期内不同时刻的涡系变化如图9所示。
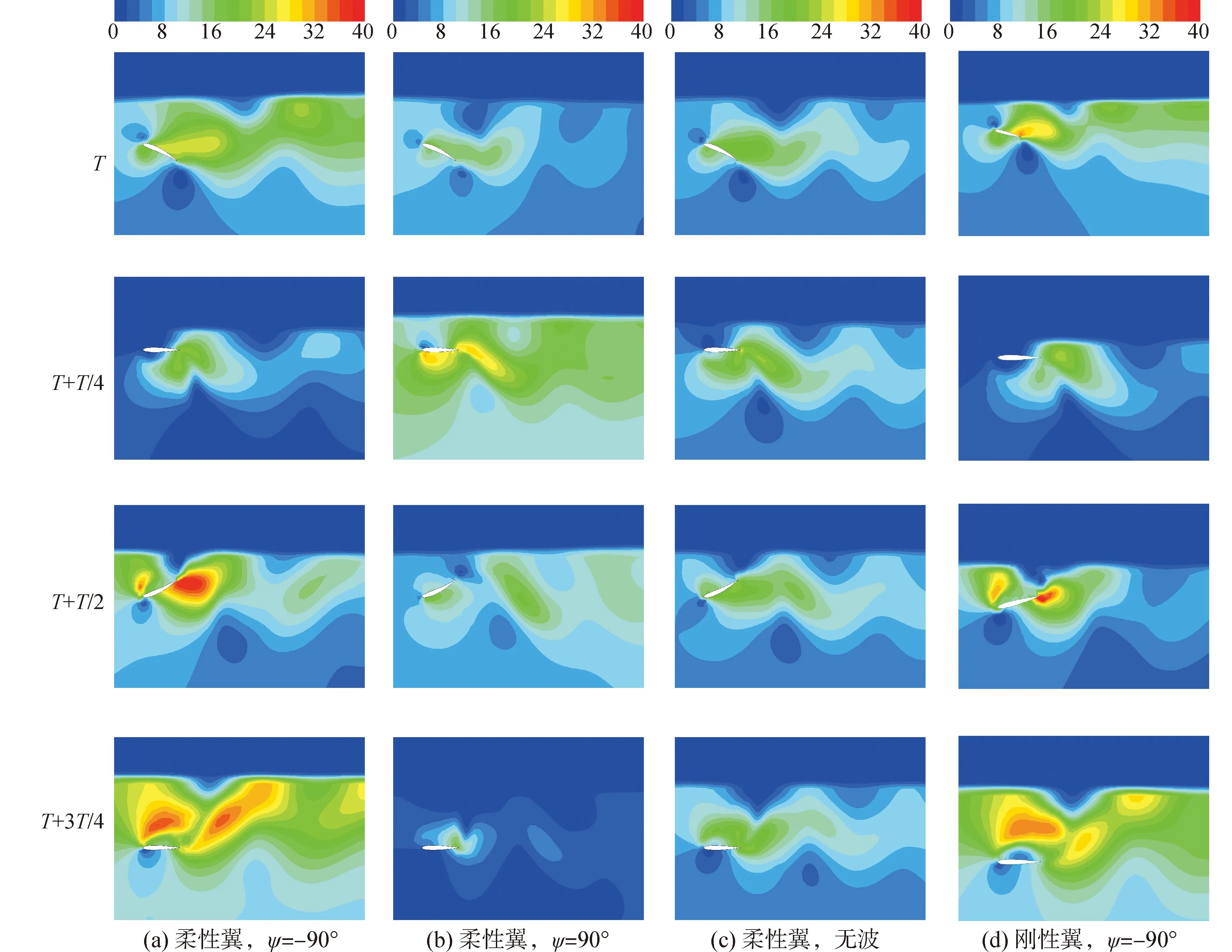
图9 一个周期内不同工况水翼表面压力分布Fig. 9 Pressure distribution of foil with different situation in one period
图9中给出了ψ=-90°时刚性翼的涡系情况作为比较。从图中可以看出水翼涡系的形成、融合、脱落及耗散过程。对比柔性翼ψ=-90°与ψ=90°两列图可知,T时刻,ψ=-90°时水翼尾涡梯度更大,对应图6中推力系数在0时刻ψ=-90°时更大;在T+T/4时刻,虽然ψ=90°水翼尾涡梯度更大,但由于此时翼首部另一侧生成了较大的首缘涡,从而产生了水翼阻力分量,导致此时两种情况下的推力系数相差不大;在T+T/2时刻,明显可以看出ψ=-90°时涡梯度远高于ψ=90°情况,对应图6中推力系数此时差别最大;同理,T+3T/4时刻由于ψ=-90°时首缘涡引起的阻力成分,导致此时两种情况下推力系数差别不大,此外ψ=-90°时尾涡分布更为连续,从而其效率较高。可见,恰当的ψ能够增加水翼涡系梯度、影响涡系结构,从而改变翼的性能情况。同理,对比ψ=-90°及无波情况下的水翼涡系可知,ψ=-90°时水翼涡系梯度更大,因而其推力也较无波时高。而由ψ=-90°时柔性翼与刚性翼涡情况可得,二者尾涡梯度差别不大,但柔性翼涡系分布更为集中、连续,即涡系能量更为集中,耗散更少,从而使得二者推力差别不大,但效率柔性翼更高。
4结论
1)波翼相位差对翼水动力系数的相位及幅值均有很大影响,主要体现在水动力系数曲线峰值的幅度及其出现时间上。翼柔性的存在能够减小其水动力系数的峰值幅度。
2)翼平均推力系数与其波浪回收功率系数均是随着ψ的增加以近正弦规律变化,峰值出现在ψ=-45°附近,谷值出现在ψ=135°附近;恰当的波翼相位差能够较大幅度提升柔性翼的推力及其对波浪能的回收功率,而不当的波翼相位差反而会损失翼自身功率;同时,相同工况下,柔性翼对波浪能的利用功率要高于刚性翼。
3)柔性翼推进效率及波浪能利用效率均随波翼相位差的增加呈正弦规律变化,在ψ=-45°附近,柔性翼对波浪能利用效率最高,在ψ=135°时,利用效率最低,ψ在-160°-45°时,柔性翼均可从波浪中获取能量;恰当波翼相位差下,翼推进效率可高于其处于无波水面下情况;任意波翼相位差下,均有柔性翼推进效率高于刚性翼,而其波浪能利用效率亦不低于刚性翼。
参考文献:
[1]苏玉民, 万磊, 李晔, 等. 舵桨联合操纵微小型水下机器人的开发[J]. 机器人, 2007, 29(2): 151-154.
SU Yumin, WAN Lei, LI Ye, et al. Development of a small autonomous underwater vehicle controlled by thrusters and fins[J]. Robot, 2007, 29(2): 151-154.
[2]TRIAN TAFYLLOU M S, TRIAN TAFYLLOU G S. An efficient swimming machine[J]. Scientific American, 1995, 272(3): 64-70.
[3]JONES K D, DOHRING C M, PLATZER M F. Wake structures behind plunging airfoils: a comparison of numerical and experimental results[C]// AIAA Meeting Paper No. 96-0078, 1996.
[4]JONES K D, PLATZER M F. Numerical computation of flapping-wing propulsion and power extraction[C]// AIAA Paper No. 97-0826, 1997.
[5]JONES K D, PLATZER M F. A experimental and numerical investigation of flapping-wing propulsion[C]// AIAA Paper No. 99-0995, 1999.
[6]LIU Pengfei. Propulsive performance of a twin-rectangular-foil propulsor in a counterphase oscillation[J]. Journal of ship research, 2005, 49(3): 207-215.
[7]于宪钊, 苏玉民, 王兆立. 基于RANS方程的对拍翼推进器推进性能分析[J]. 船舶力学, 2011, 15(5): 449-455.
YU Xianzhao, SU Yumin, WANG Zhaoli. Propulsive performance analysis of a twin-flapping-foil propulsor based on RANS equations[J]. Journal of ship mechanics, 2011, 15(5): 449-455.
[8]张曦, 苏玉民, 王兆立. 振动半圆柱尾流中的二维摆动水翼推进性能研究[J]. 船舶力学, 2012, 16(4): 333-341.
ZHANG Xi, SU Yumin, WANG Zhaoli. Research on the propulsion performance of a two dimensional flapping hydrofoil in the wake of an oscillating semicircular cylinder[J]. Journal of ship mechanics, 2012, 16(4): 333-341.
[9]刘鹏, 苏玉民, 廖煜雷, 等. 滑波航行器的水动力试验[J]. 上海交通大学学报, 2015, 49(2): 239-244.
LIU Peng, SU Yumin, LIAO Yulei, et al. Experimental study of hydrodynamic performance of unmanned wave glide vehicle[J]. Journal of Shanghai jiaotong university, 2015, 49(2): 239-244.
[10]刘鹏, 苏玉民, 刘焕兴, 等. 串列异步拍动翼推进性能分析[J]. 上海交通大学学报, 2014, 48(4): 457-463.
LIU Peng, SU Yumin, LIU Huanxing, et al. Propulsive performance analysis of tandem asynchronous flapping foil[J]. Journal of Shanghai jiaotong university, 2014, 48(4): 457-463.
[11]杨亮, 苏玉民. 粘性流场中摆动尾鳍的水动力性能分析[J]. 哈尔滨工程大学学报, 2007, 28(10): 1073-1078.
YANG Liang, SU Yumin. Hydrodynamic analysis of an oscillating tail-fin in viscous flows[J]. Journal of Harbin engineering university, 2007, 28(10): 1073-1078.
[12]张曦, 苏玉民, 王兆立. 弦向变形相位角对柔性尾鳍影响的水动力研究[J]. 哈尔滨工程大学学报, 2011, 32(11): 1402-1409.
ZHANG Xi, SU Yumin, WANG Zhaoli. Hydrodynamic research on the effects of a chordwise deflection phase angle on a flexible caudal fin[J]. Journal of Harbin engineering university, 2011, 32(11): 1402-1409.
[13]XIAO Qing, ZHU Qiang. A review on flow energy harvesters based on flapping foils[J]. Journal of fluids and structures, 2014, 46: 174-191.
[14]WU T Y. Extraction of flow energy by a wing oscillating in waves[J]. Journal of ship research, 1972, 14(1): 66-78.
[15]ISSHIKI H. A theory of wave devouring propulsion (1st report)[J]. Journal of the society of naval architects of Japan, 1982, 1992(151): 54-64.
[16]ISSHIKI H, MURAKAMI M. A theory of wave devouring propulsion (4th report)[J]. Journal of the society of naval architects of Japan, 1984, 1984(156): 102-114.
[17]DE SILVA L W A, YAMAGUCHI H. Numerical study on active wave devouring propulsion[J]. Journal of marine science and technology, 2012, 17(3): 261-275.
[18]PREMPRANEERACH P, HOVER F S, TRIANTAFYLLOU M S. The effect of chordwise flexibility on the thrust and efficiency of a flapping foil[C]//Proceedings of the 13th International Symposium on Unmanned Untethered Submersible Technology, Durham, USA, 2003: 120-128.
[19]ZHU Qiang. Numerical simulation of a flapping foil with chordwise or spanwise flexibility[J]. AIAA journal, 2007, 45(10): 2448-2457.
[20]SCHOUVEILER L, HOVER F S, TRIANTAFYLLOU M S. Performance of flapping foil propulsion[J]. Journal of fluids and structures, 2005, 20(7): 949-959.
[21]TRIANTAFYLLOU M S, TRIANTAFYLLOU G S, YUE D K P. Hydrodynamics of fishlike swimming[J]. Annual rewview of fluid mechanics, 2000, 32: 33-53.
[22]王兆立, 苏玉民, 杨亮. 黏性流场中鱼类胸鳍的水动力性能分析[J]. 水动力学研究与进展, 2009, 24(2): 141-149.
WANG Zhaoli, SU Yumin, YANG Liang. Hydrodynamic analysis of the pectoral-fins in viscous flows[J]. Chinese journal of hydrodynamics, 2009, 24(2): 141-149.
[23]ANDERSON J M, STREITLIEN K, BARRETT D S, et al. Oscillating foils of high propulsive efficiency[J]. Journal of fluid mechanics, 1998, 360: 41-72.
[24]GRUE J, MO A, PALM E. Propulsion of a foil moving in water waves[J]. Journal of fluid mechanics, 1988, 186: 393-417.
[25]WANG S, SU Y, ZHANG X, et al. RANSE simulation of high-speed planning craft in regular waves[J]. Journal of marine science and application, 2012, 11(4): 447-452.
[26]王硕, 苏玉民, 庞永杰, 等. 高速滑行艇在规则波中的纵向运动数值研究[J]. 哈尔滨工程大学学报, 2014, 35(1): 45-52.
WANG Shuo, SU Yumin, PANG Yongjie, et al. Numerical study on longitudinal motions of a high-speed planing craft in regular waves [J]. Journal of Harbin engineering university, 2014, 35(1): 45-52.
[27]BARRETT D S, TRIANTAFYLLOU M S, YUE D K P, et al. Drag reduction in fish-like locomotion[J]. Journal of fluid mechanics, 1999, 392: 183-212.
[28]ZHANG X, SU Y, YANG L, et al. Hydrodynamic performance of flapping-foil propulsion in the influence of vortices[J]. Journal of marine science and application, 2010, 9(2): 213-219.
[29]TRIANTAFYLLOU M S, HOVER F S, TECHET A H, et al. Review of hydrodynamic scaling laws in aquatic locomotion and fishlike swimming[J]. Applied mechanics reviews, 2005, 58(4): 226-237.
[30]FISH F E, ROHR J J. Review of dolphin hydrodynamics and swimming performance[R]. Space and naval warfare systems commandSan Diego CA, 1999.
[31]BORAZJANI I, SOTIROPOULOS F. Numerical investigation of the hydrodynamics of anguilliform swimming in the transitional and inertial flow regimes [J]. Journal of experimental biology, 2009, 212(4): 576-592.
[32]BORAZJANI I, SOTIROPOULOS F. Numerical investigation of the hydrodynamics of carangiform swimming in the transitional and inertial flow regimes [J]. Journal of experimental biology, 2008, 211(10): 1541-1558.
Effects of wave phase difference on the hydrodynamic performance of a flexible flapping foil
LIU Peng1,2, SU Yumin2, LI Ningyu2
(1. College of Engineering, Ocean University of China, Qingdao 266100, China; 2. Science and Technology on Underwater Vehicle Laboratory, Harbin Engineering University, Harbin 150001, China)
Abstract:Under the background of a bionic propulsion system using wave energy, in this paper we investigate the influence of the phase difference between wave and foil motion on the propulsion system of a two-dimensional flexible flapping foil near the wave surface under a regular wave. We applied the Reynolds-averaged Navier-Stokes (RANS) equation solution to analyze the hydrodynamics of a flexible flapping foil with different wave phase differences. We then compared the results with those without waves and those of rigid foil in the same working conditions. The computed results indicate that wave phase differences influence the phase angles of the hydrodynamic coefficients, as well as their magnitude. With a favorable wave phase difference, a flexible foil can improve its thrust force and efficiency by utilizing wave energy and its ability to utilize wave energy is higher than that of a rigid foil. Wake characteristics were also analyzed, and the results show that a favorable wave phase difference can improve the gradient and continuity of the wake vortex, and thereby increase the thrust and efficiency of the flexible foil under the wave surface.
Keywords:flexible foil; regular wave; wave phase difference; hydrodynamic performance; wake vortex
中图分类号:U661.43
文献标志码:A
文章编号:1006-7043(2016)03-313-07
doi:10.11990/jheu.201412064
作者简介:刘鹏(1987-),男,博士后,讲师;通信作者:刘鹏,E-mail: pengliu@ouc.edu.cn.
基金项目:国家自然科学基金资助项目(51479039,51409061);中国博士后科学基金资助项目(2013M540271);中央高校基本科研业务费专项资金资助项目(HEUCFD1403);黑龙江省博士后资助经费资助项目(LBH-Z13055).
收稿日期:2014-12-23.
网络出版地址:http://www.cnki.net/kcms/detail/23.1390.u.20160104.1427.004.html
网络出版日期:2016-01-04.
苏玉民(1960-), 男, 教授,博士生导师.

