近距平行跑道离场尾流间隔优化研究

邓文祥，潘卫军，梁海军，郑思睿，梁延安

(中国民用航空飞行学院 空中交通管理学院，四川 广汉 618307)

随着航空运输的持续发展，越来越多的国内机场都建设了近距平行跑道。近距平行跑道(CSPR)是指两平行跑道的中心线间隔小于或等于760(2 500 ft)米的跑道。截至目前为止，上海浦东国际机场、重庆江北国际机场和长沙黄花国际机场等机场均建设了近距平行跑道。但是根据中国民用航空局颁布的《平行跑道同时仪表运行管理规定》中的规定，对于近距平行跑道，航空器可能受尾涡影响时，平行跑道离场航空器的放行间隔应当按照为一条跑道规定的放行间隔执行[1]。因此对于近距平行跑道，国内机场运行仍主要是一起一降的运行模式，限制了机场容量的增长以及未发挥出来近距平行跑道对机场容量增长的作用。然而，目前FAA在西雅图机场等国际机场都已运行了相关运行模式。因此，为了发挥近距平行跑道优势，国内外众多学者对相关运行模式下尾涡风险进行了研究。

J.N.Hallock[2]对近距平行跑道上的尾流进行了相关研究，计算消散所需时间。J.Hammer[3]提出了配对进近的概念和程序，对近距平行跑道构型下，相关平行进近运行中尾涡影响前后机之间的尾涡间隔进行了研究；FAA[4]在2013年研发并应用了离场尾流缓解系统(WTMD)，WTMD的目的是通过缩减现行的尾流间隔时间来提高平行近距跑道机场容量。国内学者方面，冯志勇[5]分析了尾涡对飞行的影响以及安全间隔的研究；孙佳等[6]对近距平行跑道下尾涡的影响区域进行了研究；田勇等[7]对近距平行跑道运行间隔进行了研究；但是以上研究都未考虑当侧风分量达到一定速度时，由于有利侧风对尾流侧向运动的抑制，前机尾流无法侧向扩散到另一条平行航迹，此时后机无需考虑尾流影响，因此本文主要对此进行研究。

本文首先分析了近距平行跑道构型下飞机连续起飞时后机遭遇尾涡场景，建立侧向风速下尾涡侧向移动的时间-距离模型，建立计算后机承受尾涡能力模型，建立尾流间隔优化模型，最后以上海浦东国际机场实际风速和离场机型为例进行了验证，其结果可为动态尾流间隔的研究提供参考依据。

1 近距平行跑道飞机遭遇尾涡风险分析

在近距平行跑道上进行连续起飞时，前机产生的尾涡因为自身的扩散使得尾涡侧移到平行航迹上。但是在特定侧风的影响下，前机产生的尾涡在侧移到平行航迹之前就已经消散到后机可以承受的尾涡强度。

统计表明：绝大多数的尾涡遭遇事件发生在离地30～60 m 的近地阶段；由飞机尾涡产生机理可知，速度与飞机初始尾涡强度成反比。因此，本文选定飞机最小安全飞行速度V2作为飞机初始尾涡强度产生点的3种情形进行分析，如图1所示。

图1 后机遭遇尾涡场景示意图

情形1表示当尾涡侧移到另一条平行航迹时，其尾涡强度小于等于后机所能承受的尾涡强度，情形2表示尾涡侧移到另一条平行航迹时大于后机所能承受的尾涡强度，情形3表示尾涡在侧风作用下无法侧移到另一条平行航迹。根据上述3种场景，其后机遭遇前机尾涡风险可以表示为

(1)

式(1)中:t1表示前机尾涡侧移到另一条平行航迹时间；t2表示尾涡消散到后机所能承受强度的时间;P表示后机是否有风险，其中0表示无遭遇尾涡风险,1表示有遭遇尾涡风险。

2 尾涡形成和耗散机理

2.1 尾涡形成模型

在飞行过程中，从机翼后缘脱落的涡面，经过近场演变阶段，形成尾涡。国内外学者通过对尾涡特性的研究，建立了不同的尾涡切向速度以及尾涡消散模型，由于Hallok-Burnham尾涡模型计算简单并能精确描述尾涡的切向速度，因此使用H-B模型计算尾涡切向速度[8]。其模型如下：

(2)

(3)

(4)

式(2)中：Γ0为初始涡环量；Vθ(r)为尾涡的切向速度；W为飞机重量；g为重力及速度；ρ为空气密度；V为相对于飞机的来流速度，约等于飞机速度；B为飞机的翼展长度；r为尾涡横切面上点与涡核中心点之间的距离。

2.2 尾涡强度耗散模型

经过对尾涡实验现象的观察和对尾涡数据进行分析，可以得出飞机产生的尾涡可以分为近场涡和远场涡，当飞机处于地面效应时，地面效应会加快尾涡的耗散，为了保持一定的安全余量，本文未考虑地面影响对尾涡耗散的影响。根据Sarpkaya进行的试验观察以及数据分析，尾涡消散模型如下[9]：

(5)

式(5)中：N*表示浮力频率(Brunt-Vaisala frequency)[10];t0为基准时间;tc为尾涡开始消散时间。根据Sarpkaya提出的尾涡开始消散时间和无因此消散率之间的关系可以求得tc，关系式如下：

(6)

当ε*≥0.253 5时

(7)

当0.253 5≥ε*≥0.012 1时

(8)

当0.012 1≥ε*≥0.001时

(9)

当ε*≤0.001时：

(10)

其中：ε*为尾涡的消散率;ε为大气湍流；Vl为前机飞行速度；bl为前机的翼展长。

2.3 尾涡侧向扩散模型

尾流在大气中会向外向后扩散，因此尾流在经过一定时间后会扩散到另一条平行航迹。在起飞过程中，前机产生的尾涡具有一定的初始宽度，根据Vernon J.Rossow等[11]对尾涡初始宽度分析后得出：

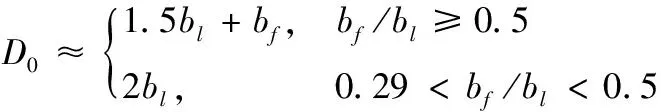
(11)

式中：D0为起始尾涡危险区域宽度；bf为后机的翼展长度。

当尾涡处于地面效应内时，尾涡在地面效应的影响下会以一定的速度向两侧移动，增大尾涡危险区域宽度。当有侧风时，前机产生的尾涡会在侧风的作用下侧移到另一条平行航迹上，进而改变尾涡危险区域宽度。同时由于尾涡自身会在大气环境下进行扩散，也使得尾涡危险区域增大。为了提高安全性，本文增加了安全余量，以保证尾流间隔的安全性。本文考虑尾涡间隔安全余量d和导航系统造成的误差d1。综上所述，前机尾涡侧移到另一条跑道时间满足：

(12)

式中：D为平行跑道两中心线间距；Dt1表示尾涡在大气环境影响下自身侧翼宽度；W为侧风风量-W表示不利侧风；+W表示有利侧风；Vd为地面效应下尾涡的侧向移速，通常取2 m/s；

3 起飞尾涡间隔优化模型

对于飞机遭遇尾涡的情形，最危险的情况是飞机进入到前机一个尾涡的中心。飞机在离场阶段，飞机遭遇尾涡的高度通常较低，此时遭遇尾涡是很危险的情况。因此本文研究的是进入到单个尾涡中心并处在离场阶段的情况。

本文使用基于条状带方法的空气动力学交互作用模型对尾涡诱导滚转力矩进行研究[12]。在条状带模型中，忽略机身，飞机简化为机翼，水平和垂直的尾部表面。图2表示了简化的飞机模型。对于每个条形元件，计算涡流引起的迎角。条状带模型实现了最大迎角的特殊限制，以防止局部迎角超过最大的迎角限制。

图2 条状带模型

本文对于尾涡诱导力矩的计算围绕着力矩基本原则，即一个力矩乘以某个距离(力矩臂)。因此，对于机翼仅由尾涡产生的滚动力矩表达如下：

M=L×F

(13)

式中：M表示尾涡产生的滚转力矩;L表示机翼上某点距机翼中心的位置；F为尾涡的诱导滚转力，等于由尾涡改变的飞机升力。

由条状带法思想，计算一个条带上由尾涡引起的升力变化量，进而得到此条带上的诱导力矩：

(14)

ΔMv=dΓ(y)·y=

(15)

其中：dΓ(y)表示为局部的升力变化量；ΔMv为局部诱导力矩；Vf为空气的来流速度，约等于飞机的飞行速度；cl(y)表示处于y位置处的升力线系数；c(y)为弦长；Δα(y)表示迎角变化量。

由于迎角变化量很小，近似等于：

(16)

式中：Δα(y)表示尾涡引起的迎角变化量。

通过Ivan De Visscher等[13]的研究，翼型对诱导滚转力矩影响差别不大。故本文对椭圆翼弦进行计算：

(17)

式中c表示为飞机的平均翼弦。

将式(16)和式(17)代入式(15)并积分后可得尾涡对飞机产生的诱导力矩Mv：

(18)

遭遇的严重性标准应该能够比较各种类型的飞机，因此需要一个无量纲化参数。然而如果直接通过尾涡产生的诱导力矩与飞机的侧倾控制力矩进行比较，对不同类型的航空器来说，很难得出一个统一的标准。因此本文采用滚转力矩系数这一无量纲化参数去比较具有不同物理和空气动力学特性的飞机之间遭遇尾涡的严重性程度。

滚转力矩系数RMC是一个与飞机飞行速度、翼展以及机翼面积有关的无量纲系数，其计算模型如下：

(19)

将式(18)代入式(19)可得：

(20)

当得知飞机周围的尾涡强度时，可以计算出所承受的RMC值。同时当得知飞机所能承受的最大RMC值时，可以求出飞机所能承受的最大尾涡环量。

根据近距平行跑道起飞尾涡遭遇场景分析可知，当有利侧向风速分量大于一特定值时，在实施连续起飞时无需考虑尾流的影响，只需考虑前后机之间的碰撞安全间隔。当存在不利侧向风速且大于某一特定值时，需要考虑尾流侧向移动时间与尾涡强度耗散到后机可承受强的时间的关系，因此尾流间隔优化模型为

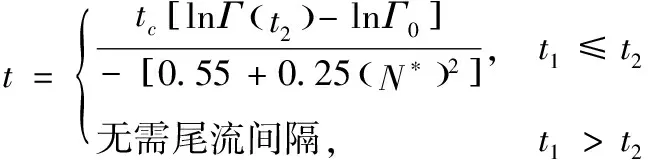
(21)

4 实例分析

上海浦东国际机场34L/16L和34R/16R跑道为近距平行跑道，跑道长度为3 800 m，中心线间距为440 m，如图3所示。

图3 上海浦东机场16L(R)跑道示意图

通过对上海浦东国际机场7日航班量统计，选取占比重较大的机型，如图4所示，可以发现使用量最大的机型为A321和A320。由于目前同类机型无离场尾流间隔规定，因此本文选取机型为A330和A321，并假设A330为前机在16L跑道起飞，A321为后机在16R跑道起飞，机型参数如表1所示。取A321可承受滚转力矩系数为0.046[14]，计算出所能承受的尾涡强度为180 m2/s。所取浮力频率和不同等级湍流度数据如表2所示。统计上海浦东机场的七日机场风向数据作为分析数据，化为垂直于跑道的侧向风量，以0.5 m/s为一个区间进行统计，并将5 m/s及以上风速数据统计到5 m/s中，如图5所示，不同侧风分量下尾流侧移到另一条平行航迹时间如表3所示。

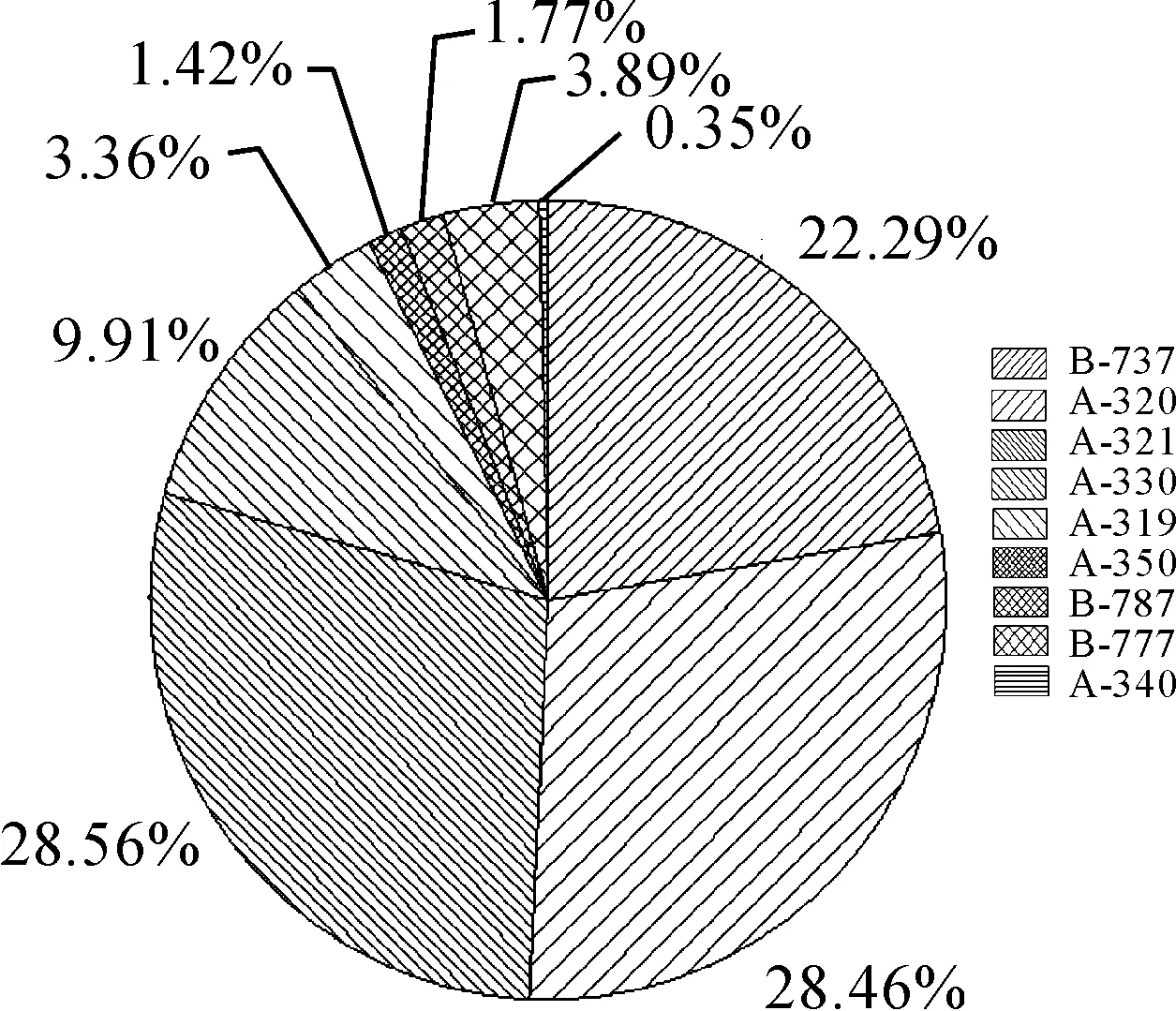
图4 上海浦东机场7日出港航班机型百分率

表1 前后机机型参数

表2 到达后机承受尾涡强度所需耗散时间

图5 上海浦东机场七日侧向风速统计

表3中不利侧风为加速尾流侧移到后机航迹的正侧风分量，文中风向为16L吹向16R；有利侧风为抑制前机尾流侧向扩散到后机航迹的正侧风分量，文中风向为16R吹向16L。

根据FAA ORDER JO 7110.316规定，当前机为重型机或B-757，且跑道头间距错开小于500 ft时，前机起飞2 min后后机才可以起飞。从表2可以看出：当在弱湍流度条件下时，不同的浮力频率下所需的时间皆大于目前规定的120 s尾流时间间隔，当处于中、强湍流度等级下，消散所需时间皆小于120 s，因此当处于中、强等级的湍流度时可以将尾流间隔缩减至100 s以下。

从表3可以看出，随着不利侧风分量的逐渐增大，尾涡侧移到另一条跑道的时间越来越短，当左侧风速到达5 m/s时，侧移到另一条跑道只需36 s的时间。当存在有利侧风分量时，侧风抑制尾流扩散，使得侧移时间变长，当有利侧风风速分量为2 m/s时，侧移时间需要292 s，远大于目前法规规定的时间，据统计可知，七日内有24.77%的时间无需考虑前机尾流影响。

表3 不同风速下尾流侧移时间

注：*表示时间大于292 s

从表2和表3可以看出，当存在不利侧风时，尾流在120 s内均可扩散到另一条跑道上，但当在中、强湍流度等级条件下，根据大气湍流等级的不同，飞机连续起飞时间间隔可缩减至100 s，因此湍流等级在中湍流度和强湍流度等级时可以缩减现有尾流间隔时间。当存在有利侧风时，当风速大于等于2 m/s时，连续起飞的航空器可以不必考虑尾流的影响，只需要保持碰撞安全间隔。

5 结论

1)当在静风、不利侧风分量以及有利侧风分量小于2 m/s条件下，前后离场航空器需要考虑尾流间隔。但在弱湍流等级下，需要适当提升现行尾流时间间隔；在中、强湍流度等级下，尾流时间间隔可缩减至100 s。

2)当有利侧风分量达到2 m/s时，前机尾流无法侧移到另一条平行航迹上，前后机无需保持尾流时间间隔，只需保持碰撞安全间隔。