二元函数与一元函数的几个转化问题*

叶建兵

(南京理工大学 泰州科技学院，江苏 泰州 225300)



二元函数与一元函数的几个转化问题*

叶建兵

(南京理工大学 泰州科技学院，江苏 泰州 225300)

摘要：讨论了二元函数与一元函数在极限、增量、积分等方面的几个转化问题，特别指出应慎重使用极坐标计算二元函数极限，并辅以实例加以说明。

关键词：二元函数；一元函数；极限；方向极限；增量；积分；转化

0引言

二元函数微积分与一元函数微积分是高等数学教学的主要内容，通常在教学过程希望学生注意两者之间的联系与区别。本文将介绍二元函数与一元函数在极限、增量、积分等方面的几个转化问题，分析讨论文献中的一些结论，指出已有文献中关于二元函数极限的一个谬误，并辅以实例加以说明，展示转化想法的巧妙，以及给解题带来的方便。

1二元函数极限转化为一元函数极限

文献[1]提出了一种将二元函数极限存在性的判断及求法转化为一元函数极限的方法，主要结论如下：

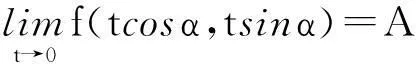
当α∈[0,2π]，且α≠0，π，2π时，

当α∈[0,2π]，且α=0，π，2π时，

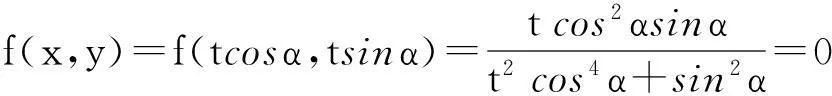
因此，沿着直线l，不管α∈[0,2π]取何值，当t→0+，总有f(x,y)→0。

(2)取抛物线路径y=kx2，k≠0，则

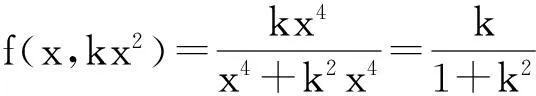
此时有

对于在计算二元函数极限时能否使用极坐标的问题，文献[4]认为若动点(x,y)的极径t→0+时，幅角α∈[0,2π]具有任意性，这样就保证了动点(x,y)趋向于定点(x0,y0)的路径具有任意性。这一观点比较粗糙，表述也比较模糊，易使人误解其结论与文献[1]相同。

为讨论二元函数极限与一元函数极限的关系，给出“方向极限”的定义。

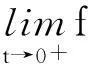
例1表明方向极限存在尚不能保证二元函数极限的存在性，需要加强条件。

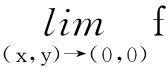
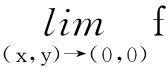
下面的定理3精确地解决了能否用极坐标计算二元函数极限的问题，其中第二个条件实际上给出了幅角一致性的一个判别方法。

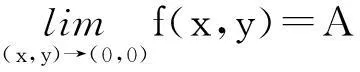
至此，本文纠正了文献[1]的谬误并澄清了文献[4]的结论：方向极限的存在性不能推出二元函数极限的存在性，不能轻易地把极坐标方法求出的方向极限作为二元函数的极限，用极坐标方法求二元函数的极限应慎重。

2二元函数增量转化为一元函数增量

对于二元函数问题中经常涉及到的函数值增量f(x2,y2)-f(x1,y1)，可以用“直线法”将该增量形式转化为一元函数的增量[6]。令

x=x1+t(x2-x1)，y=y1+t(y2-y1)，t∈[0,1]，

这种表示法实质是利用了连接(x1,y1)与(x2,y2)两点线段的参数方程。由于(x1,y1)，(x2,y2)是固定的两点，于是，

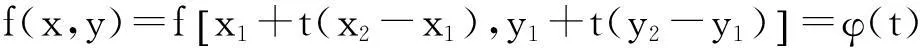
二元函数的增量f(x2,y2)-f(x1,y1)转化为一元函数φ(t)在[0,1]上的增量：

f(x2,y2)-f(x1,y1)=φ(1)-φ(0)。

用此方法证明例2(二元函数的拉格朗日中值定理)和例3(二元函数的柯西中值定理)[7]，例2是2012年江苏省普通高等学校非理科专业高等数学竞赛试题。

例2设函数f(x,y)在平面区域D上可微，线段PQ位于D内。已知点P、Q的坐标分别为(a,b)、(x,y)，求证：在线段PQ上存在点M(ξ,η)，使得

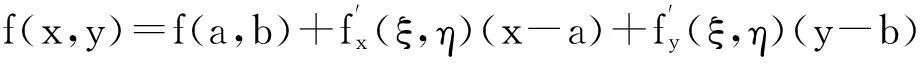
f(x,y)-f(a,b)=φ(1)-φ(0)。

因φ(t)在[0,1]上连续，在(0,1)内可导，则存在θ∈(0,1)，使得

f(x,y)-f(a,b)=φ(1)-φ(0)=φ′(θ)(1-0)=φ′(θ)。

另一方面，由全导数的计算，得

令ξ=a+θ(x-a)，η=b+θ(y-b)，则

因θ∈(0,1)，则点M(ξ,η)一定位于线段PQ上，从而

移项即得二元函数的拉格朗日中值定理。

例3[7]设二元函数f(x,y)和g(x,y)满足：(1)在点P0(x0,y0)处连续；(2)在去心邻域Uo(P0,δ)内可微，dg≠0，则对∀P(x0+Δx,y0+Δy)∈Uo(P0,δ)，存在ξ=x0+θΔx，η=y0+θΔy，θ∈(0,1)，使得

证用直线法引进两个辅助函数

φ(t)=f(x0+tΔx,y0+tΔy)，ψ(t)=g(x0+tΔx,y0+tΔy)，

则

对上式的右端用一元函数的柯西中值定理，得

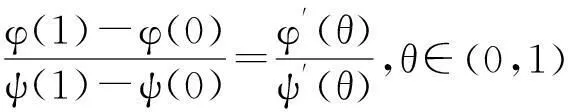
仿例2求全导数的计算，得

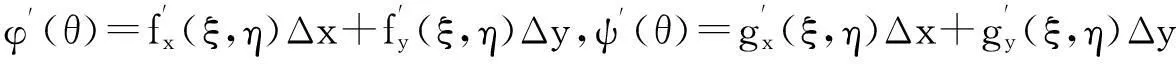
且ξ=x0+θΔx，η=y0+θΔy．综上即得二元函数的柯西中值定理。

事实上，这里将二元函数增量转化为一元函数增量的方法是微积分中的经典方法。多元连续函数的性质、多元函数的微分中值定理(包括多元函数泰勒公式)等的推导用的就是这种方法。就平面区域而言，该方法的本质是平面区域的连通性保证了其上任意两点可用含于其内的直线(折线)连接起来，从而当二元函数被限制在直线(折线)上时可转化为一元函数问题进行讨论[8]。

3一元函数定积分转化为二重积分

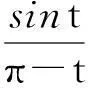
另一方面，若将

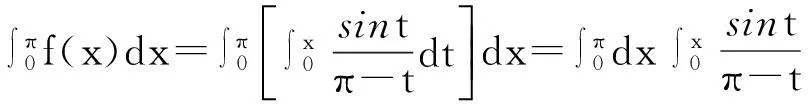
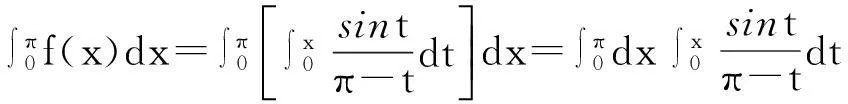
证注意到

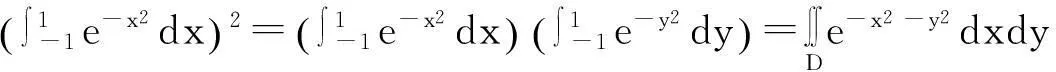
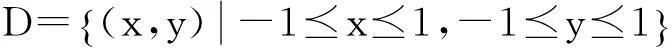
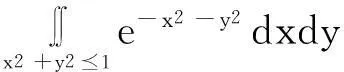
容易求得

从而

4结语

本文讨论了二元函数与一元函数在极限、增量、积分等方面的几个转化问题。针对已有文献提出用极坐标求二元函数极限的方法，通过对二元函数极限本质及实例的分析，本文指出了其中的谬误，讨论并澄清了方向极限与二元函数极限的关系，特别指出应慎重使用极坐标方法计算二元函数极限．其他的两个转化问题则显得非常巧妙，通过有效的转化建立起新旧知识之间的联系，可以从新的角度认识问题，常使人有“柳暗花明又一村”的感觉。

参考文献：

[1]丁殿坤，吕端良，李淑英．多元函数极限的一种求法[J]．南阳师范学院学报，2004，3(12)：25-27.

[2]蔡燧林．高等数学例题精选：高等数学竞赛培训教程[M]．北京：清华大学出版社，2011.

[3]华东师范大学数学系．数学分析：下册[M]．3版．北京：高等教育出版社，2001.

[4]罗俊芝．能否用极坐标方法求二重极限[J]．高等数学研究，2007，10(2)：18-19，27.

[5]裴礼文. 数学分析中的典型问题与方法[M]．北京：高等教育出版社，1993.

[6]石秀文．转化思想在数学分析中的应用[J]．高等数学研究，2014，17(2)：31-35.

[7]李勇，汪民乐，杜萍．多元函数的L′Hosipital法则及应用[J]．大学数学，2012，28(3)：123-127.

[8]尹洪武，张步英，王群.一类非线性抛物方程的高精度有限元分析[J].河北科技师范学院学报，2013(2)：53-57.

责任编辑：程艳艳

Some Transformations between Binary Function and One Variate Function

YE Jianbing

(Taizhou Institute of Science and Technology, Nanjing University of Science and Technology, Taizhou 225300, China)

Abstract：This paper discusses the transformations between binary function and one variate function in terms of limit, increment and integration. Particularly, it is pointed out that the polar coordinate should be carefully used to calculate the limit of binary function. Several examples are given to explain the transformations.

Keywords：binary function; one variate function; limit; directional limit; increment; integration; transformation

中图分类号：O172

文献标志码：A

文章编号：1009-3907(2016)02-0023-05

作者简介：叶建兵(1981-)，男，江苏泰兴人，讲师，硕士，主要从事多尺度几何分析与图像处理研究。

基金项目：2015年江苏省高等教育教改研究立项课题(2015JSJG565)

收稿日期：2015-10-26