均匀带电球壳球面电场强度计算方法的讨论

何志巍　李 纯

(中国农业大学理学院应用物理系　北京　100083)

崔文宏

(中国农业大学生物学院　北京　100193)

金仲辉

(中国农业大学理学院应用物理系　北京　100083)



均匀带电球壳球面电场强度计算方法的讨论

何志巍李 纯

(中国农业大学理学院应用物理系北京100083)

崔文宏

(中国农业大学生物学院北京100193)

金仲辉

(中国农业大学理学院应用物理系北京100083)

摘 要：综述近20年来大学物理教学中，关于均匀带电球壳表面电场强度的讨论，概括出3种常见的解法，探讨了不同解法所得不同结果的本质，确定均匀带电球壳表面电场强度的最佳算法.

关键词：均匀带电球壳电场强度积分方法

对于一个均匀带电的非导体球壳，根据高斯定理很容易得出球壳内外的电场强度，但是球壳表面电场强度分布是什么样的呢？显然，知不知道这一点的场强对于很多实际工作并不会有太大影响，但基于物理知识体系的完整性，我们有必要探讨一下这类问题，因为很多理论都是源于某些奇点、临界问题的解决而得以发现或发展的.

1方法与结论

1.1方法一

文献[1～4]都提到了这样一种最为普遍的解法，如图1所示,P为球面上任意一点，以球心O为极点，射线OP为极轴，在过球心O和点P的空间任意一个平面里建立极坐标系，其中点A(R,θ)为截面圆上除点P以外的任意一点，A点对应的球面圆弧带电量记为dq, 易知圆弧中心点M与P点距离为R(1-cosθ).

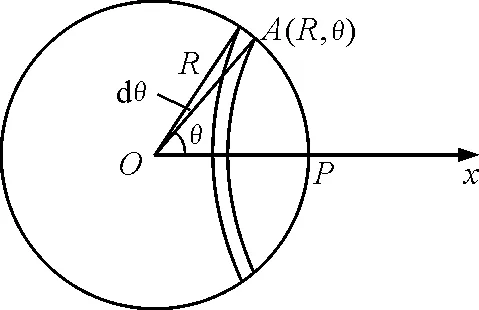
图1　点电场中P点的电场强度

已知一个带电量q，半径r的均匀带电圆环，其在垂直于环面的轴线上距圆环中心为x处的点P电场强度为如图2所示，则

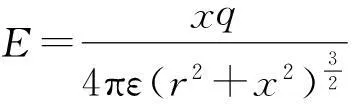
(1)

那么，图1中圆弧在P点产生的电场强度

(2)

(3)

所以，P点电场强度

(4)

图2　环形电场中P点的电场强度

1.2方法二

文献[5]通过功能原理求解该问题也得到了同样的结论：

图1中，设想把带电球面从半径为R缓慢地收缩到半径为R-dR这一状态, 则克服电场力做的功为dW=qEdR,E为球面上的电场强度.球面半径减小dR后，距球心大于R处的电场强度及场的能量不发生变化，则该过程中克服电场力做的功转变为收缩区域的电场能，即有(ER为收缩之后，距离球心为R处的电场强度)

(5)

由高斯定理可知

(6)

所以

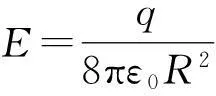
(7)

1.3方法三

除了前两种方法外，文献[2]还提及另外一种解决问题的思路.图1中由高斯定理得出

(8)

文献[2]和文献[6]还先后提到一种较为真实的球层模型，得出电场强度在球壳表面发生突变这一结论.如图3所示,横轴表示A点距离球心O距离x, 纵轴表示相应空间电场强度大小E，E在x=R处发生跃变.

图3　球壳表面电场强度与球心距离的关系

2分析与讨论

首先值得关注的是，文献[2]提出另外一种合乎情理的解法，所得结果与其他两种方法不同.笔者开始也是用这种类似的极限，求解出了相同的结果.那么，到底哪一种结论是对的呢？

文献[6]认为讨论球壳表面电场强度没有意义，原因在于球壳模型是假想的而非现实存在的.一个均匀带电球层(厚度为r)只有当其电场力作用点离它很远，即d≫r时(图3)，球层厚度才可以忽略不计，此时变为球壳模型.而当A无限靠近球层表面时，球层将不能看做球壳.此时球层内外表面及内部电场强度分布均可以通过高斯定理求出，球层电场强度在整个空间连续分布(图4,5).因而实践中根本不存在所谓的球壳表面电场强度分布的问题.文献[2]也得出了同样的结论.

图4　均匀带电球壳无限远处的电场强度

图5　球层在整个空间的电场强度的分布

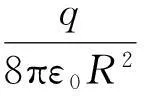
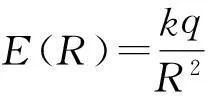
方法一中，当带电圆环无限靠近P点以致到达P点时，该圆环在P点电场强度dE将不再是基于库仑定律和叠加原理推出来的

(9)

图6　P点所在处

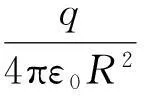
事实上，求均匀带电球壳q外面的电场强度时，将均匀带电球壳看做一个位于球心，带电量为q的点电荷，所得电场强度结果完全相同.这说明在一定程度上，均匀带电球壳模型可以看做点电荷模型.用空间广阔的尺度去看，求球壳表面电场强度，无疑和求点电荷所处位置电场强度相同.

当然以上从数学角度将点电荷与球壳联系起来可能会觉得有点牵强，那么不妨回归球壳模型本身.将球壳看成无数个点电荷的集合，此时求球壳表面电场强度与求点电荷在空间所处位置电场强度将没有什么本质的区别.

莫非该问题真的无解？

方法二中文献[5]通过功能原理，绕过库仑定律成功地求解了该问题.它的思路一定程度上是经得起推敲的.思路中所提及的几个物理量：电场强度E, 电场力做功W, 都不是在库仑定律基础上提出来的概念，只是通过库仑定律，能进一步揭示这些物理量之间的关系.再者，在电场能量表达式推导的过程中，每一个物理量定义及规律的基础也都与库仑定律没有必然的联系[9].以严格的物理定义和公认的数学逻辑为基础，该思路的完备性便体现于此！从而也可以得出方法三中的电场强度空间分布在球壳模型中是不连续的.

那么进一步讲，均匀带电球层在空间的电场强度是如何分布的呢？是连续还是间断？其实结果是不得而知的.球层内外电场强度的计算固然没有问题，但球层内部与球层内外表面电场强度分布的计算缺乏数学基础.我们知道球层电荷体密度值，但一个曲面是没有体积的，我们无法得出球层内外表面及球层内部高斯面上的电荷量.结果自然无法应用文献[5]推出的结论.这是数学几何基础上的缺陷或局限.假设我们定义一个点是有长度，有面积的；一个面是有体积的，那么以上问题表面上看就可以得到解决.但是又会遇到其他问题，毕竟我们的数学几何基础变了，很多规律将换上新的面孔.

由球壳表面电场强度问题延伸到无限长均匀带电圆柱表面电场强度问题，其解法颇为类似，同样可以推出利用功能原理求解是比较科学合理的.使用功能原理时不一定要假设圆柱面收缩，假设圆柱面膨胀也是可行的，在此不多赘述.

3结论

参 考 文 献

1施传柱. 面电荷存在处电场强度的计算. 曲靖师专学报，1993,2(12)：42～44

2史守华. 电荷面分布模型和电场强度跃变的讨论. 安徽大学学报，2001,4(25)：62～66

3彭海鹰. 均匀带电球面的电场强度分布再讨论. 物理与工程，2003,1(13)：60～61

4白俊彪. 均匀带电球面上电场强度的计算. 思茅师范高等专科学校学报，2005,3(21):79～80

5金仲辉. 均匀带电球面上的电场强度如何计算. 现代物理知识，2002(4):42

6李配军. 均匀带电球面的电场场强分布再讨论. 物理与工程，2003,6(13)：49～50

7欧几里得. 几何原本. 燕晓东译.北京：人民日报出版社，2005.26～27

8同济大学应用数学系. 高等数学(第5版)(上册). 北京：高等教育出版社，2001.59～62

9金仲辉，柴丽娜. 大学基础物理学(第3版). 北京：科学出版社，2010.128～157

Discussion on the Calculation Method of the Electric Field Intensity on Surface of Evenly-charged Spherical Shell

He ZhiweiLi Chun

(Department of Applied Physics, College of Science, China Agricultural University, Beijing100083)

Cui Wenhong

(College of Biology, China Agricultural University, Beijing100193)

Jin Zhonghui

(Department of Applied Physics, College of Science, China Agricultural University, Beijing100083)

Abstract：Review some discussion on electric field on the surface of evenly-charged spherical shell within 20 years, summarize and analyze three common solutions to ensure correct answer to this problem.

Key words：evenly-charged spherical shell；electric field; integration method

(收稿日期：2015-11-10)