化归思想在初中数学解题中的有效应用

叶玉妹

摘 要： 化归思想就是在面对数学问题时用到的一种解决手段，即将复杂的问题变简单，将抽象的问题变具体，将生疏的问题变熟悉，将一些无处下手的问题通过化归思想转化为比较容易解决的问题，能够增强学生分析问题、解决问题的能力.化归思想是数学学习中的一种常用思想，在初中数学教学过程中渗透化归思想，有利于培养学生良好的创新思维能力.

关键词： 初中数学 化归思想 有效作用

化归思想是数学中最基本的思想方法.数学中一切问题的解决都离不开转化与化归，数形结合思想体现了数与形的相互转化；函数与方程思想体现了函数、方程、不等式间的相互转化；分类讨论思想体现了局部与整体的相互转化，这三种思想方法都是转化与化归思想的具体体现.因此转化与化归是数学思想方法的灵魂，也是中考命题中重点考查的一种数学思想，下面结合有关中考试题，介绍几种常用的转化策略.

一、“数”与“形”的相互转化

“数”与“形”反映了事物两方面的属性，“数缺形时少直观，形少数时难入微”，数与形的相互转化、相互联系，体现了数学是一个有机整体.数形结合能把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来.因此，教师应努力探索，引导学生通过“数”与“形”的相互转化，探索出一条合理而乘势的解题途径，消除学生的困惑，培养学生的数学能力.如笛卡尔通过建立坐标系，确定了平面上的点与有序实数对的一一对应关系，把几何问题转化为代数问题，由此我们可以把判断点P（6，3）是否在抛物线上的问题，变成判断是否是方程的解；求直线与双曲线的交点问题，变成求方程组解的问题.

二、生疏向熟悉转化

数学题目成千上万，我们不可能全部做遍，但我们可以通过一定量的练习，掌握它们的解法，这样就拥有了会解大量数学题的能力.解题能力实际上是一种创造性思维能力，这种能力的关键是能否细心观察，运用过去所学的知识，将生疏问题转化熟悉问题.因此教师应深刻挖掘量变因素，将教材中抽象的知识利用学过知识，加工到使学生通过努力能够接受的水平上来，收到摘 要： 化归思想就是在面对数学问题时用到的一种解决手段，即将复杂的问题变简单，将抽象的问题变具体，将生疏的问题变熟悉，将一些无处下手的问题通过化归思想转化为比较容易解决的问题，能够增强学生分析问题、解决问题的能力.化归思想是数学学习中的一种常用思想，在初中数学教学过程中渗透化归思想，有利于培养学生良好的创新思维能力.

关键词： 初中数学 化归思想 有效作用事半功倍的效果.如我们学习有理数的运算是先学加法运算，而减法运算是通过化归成已学习的加法来运算.同理，把除法运算转化为熟悉学过的乘法运算等.

又如把若干个人之间握手总次数（单握）称为“握手问题”，那么像无三点共线的n个点之间连线；共端点射线夹角（小于平角的角）个数；一条线段上有若干个点形成的线段的条数；足球队之间单个循环比赛场次等问题都可转化为“握手问题”.

三、复杂向简单转化

数学解题的过程是分析问题和解决问题的过程，对于较难（繁）的问题，可以通过分析，将问题转化成几个难度与学生的思维水平同步的小问题，再根据这几个小问题之间的相互联系，以局部知识的掌握为整体服务，从而找到解题捷径.例如，求解二元一次方程组、一元二次方程时运用“未知向已知转化”的方向，把“多元问题”转化为“一元问题”、把“二次问题”转化（降次）为“一次问题”；解分式方程时，通过去分母，把“分式方程”转化为“整式方程”，实现从“复杂向简单”的转化.

四、一般向特殊转化

从特殊到一般，从具体到抽象是研究数学的一种基本方法.在一般情况下难以发现的规律，在特殊条件下比较容易暴露.而特殊情况下得出结论、方法也往往可以推广到一般情形.所以特殊和一般之间的转化可以用来验证命题的正确性，探索解题途径.

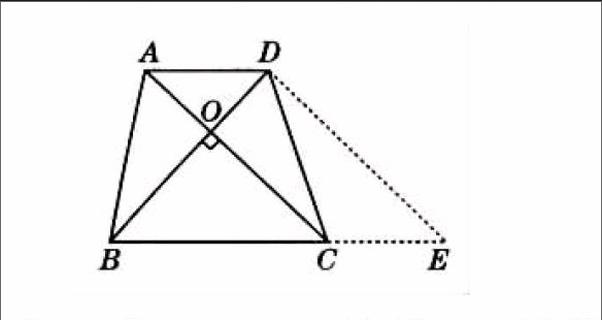
例：如图，梯形ABCD中，AD∥BC，AB=CD，对角线AC、BD相交于O点，且AC⊥BD，AD=3，BC=5，求AC的长.

分析：过D作DE∥AC交BC的延长线于E，则得AD=CE，AC=DE.所以BE=BC+CE=8，AC=4.此题是根据梯形对角线互相垂直的特点通过平移对角线将等腰梯形转化为直角三角形和平行四边形，使问题得以解决.

五、生活向数学转化

《新课标》指出：“数学是人们生活、劳动和学习必不可少的工具，能够帮助人们处理数据、进行计算、推理和证明，数学模型可以有效地描述自然现象和社会现象.”重视数学知识的应用，加强数学与实际的联系.在解决实际问题时，要重在分析，把实际问题转化为数学模型，培养学生应用数学知识解决实际问题的能力.

例：（2010中考题）某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似地看作一次函数：y=-10x+500.

（1）设李明每月获得利润为w元，当销售单价定为多少元时，每月可获得最大利润？

（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？

（3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？

分析：（1）要解决每月可获得最大利润问题，也就是把实际问题转化二次函数的极值问题.

（2）要解决“每月获得2000元的利润，那么销售单价应定为多少元？”问题，即转化为列一元二次方程解应用题问题（x-20）·（-10x+500）=2000.

（3）要解决售价、获利的在一定范围内的所需成本最低这一实际问题，则需将本题转化一次函数、二次函数有关性质来完成.

综上所述，转化思想贯穿在数学解题的始终，而转化思想具有灵活性和多样性的特点，没有统一模式可遵循，需要依据问题提供的信息，利用动态思维寻求有利于问题解决的变换途径和方法，所以学习和熟悉转化的思想，有意识地运用数学变换方法，灵活地解决有关数学问题，将有利于提高数学解题的应变能力和技巧.