巧用化归思想 提高课堂效率
许丽琼
[摘 要]在小学数学教学中,教师因课程的实际需求,很多时候会运用化归的数学思想,主要包括化难为易、化抽象为直观以及化整为零等方法。将化归思想运用于数学教学中,可以有效提高学生的理解能力,提高课堂效率。
[关键词]数学教学 问题解决 课堂教学 化归思想
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2016)35-044
化归思想就是在遇到问题时,通过转化和归类的手段将问题简单化、直观化、明朗化,从而解决问题的思想方法。小学生的认知水平有限,形象思维优于抽象思维,而数学是一门抽象性较强的学科,所以教师在教学时须结合学生的认知特点,尽可能引导学生学会将问题简单化、直观化,提高解题能力。教师在课堂教学中恰当地运用化归思想可以有效地激发并保持学生的学习兴趣和信心,提高教学效果。
一、将复杂问题简单化
在数学学习过程中,学生要善于将复杂的问题简单化。对于小学数学教学来说,学生往往要根据已知条件将问题进行转化,才能理清思路,从而运用已有的知识进行解答。
例如,在进行长方体相关知识的教学时,有一道习题:有一个封闭水箱(如右图所示),水箱的周边镶有铝条,那么做成这个水箱一共需要多长的铝条?需要多少平方厘米的铁皮?
这是一个和实际生活相关联的数学问题,要想解决这个问题,首先要对题中的条件进行化归,将复杂问题简单化。根据文字和图形我们可以知道,题目的已知条件是水箱的长宽高,求所需的铝条长度,其实是求长方体的棱长之和;求所需的铁皮面积,实际上是求长方体的表面积。
上述案例中,经过转化,一个复杂的问题变得简单易求,学生的解题思路变得明朗。由此可知,化归思想可以有效地降低问题的难度,提高课堂教学效率,同时还能提高学生在生活中实际中运用数学知识的能力。
二、将整体问题局部化
很多问题,如果从整体去进行思考和分析会非常困难。此时我们可以利用化归思想,按照一定的规律和需要将问题划分为若干个小问题,然后通过求解这些小问题找到原问题的答案。
例如,在解答“小红和爸爸的年龄差是32岁,五年后,小红的年龄将会是爸爸年龄的三分之一,那么小红和爸爸今年的年龄各是多少岁?”这道题时,学生读完题目后都感觉条件很多,但却不知道这些条件应该怎样使用。于是我根据化归思想,引导学生将问题进行分解: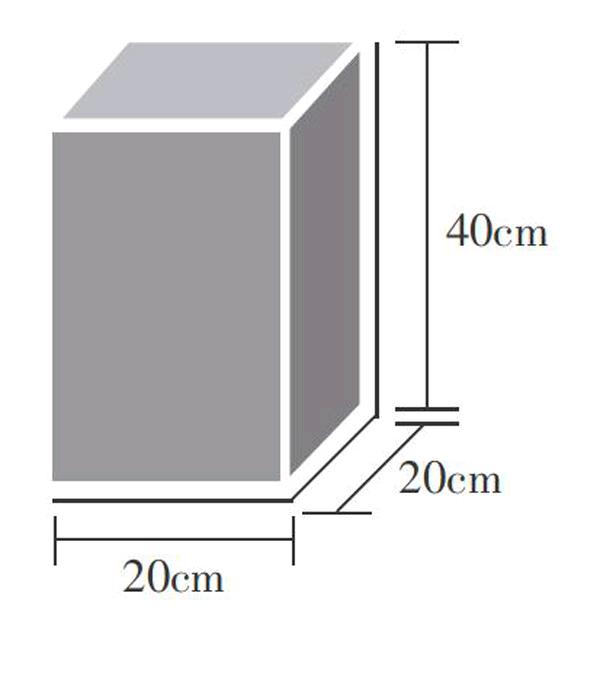
(1)小红和爸爸的年龄差可以怎样列式?
(2)五年后,小红和爸爸分别是多少岁?
(3)五年后,小红的年龄和爸爸的年龄存在什么关系?
通过这样分解,学生很快就理清了题目中的数量关系,求出小红和爸爸今年分别是11岁和43岁。
由此可见,在进行问题的解决教学过程中,可以利用化归的思想将抽象的和复杂的问题进行分解,然后逐个击破,学生也可以更好地对问题进行分析和解答,在提高解题能力的同时提高课堂的教学效率。
三、将模糊问题明朗化
数学问题的很多条件都是隐藏的,需要学生全面审题,进行仔细的推敲和分析。这时,教师可引导学生运用化归的思想对题目中的隐含条件进行分析。
例如,在解答“第一组正方形:□□□□□□;第二组正方形:第一组比这一组少2个正方形;第三组正方形:第二组比这一组多4个正方形。求第二组和第三组分别有多少个正方形。”这个问题时,学生感觉题目的信息很多,而且很乱,一时半会都不懂该怎么做。对此,我引导学生运用化归思想,找出每个条件的实质:第一组有6个正方形,第二组比第一组多2个正方形,第三组比第二组少4个正方形,求第二组和第三组各有多少个正方形。这样转化之后,题目被明朗化,学生很快就掌握了问题的本质,从而解决问题。
上述案例中,化归思想的运用,使隐藏的解题信息明朗化,将问题的本质显现出来,降低了问题的难度。由此可见,运用化归思想解决问题是可行的方式,是提高课堂的教学效率有效手段。小学生的理解能力有限,往往不能发现题目隐藏的已知条件,需要教师培养他们运用化归思想转化问题的意识,才能帮助他们突破这个障碍。
总而言之,化归思想是数学思想方法的重要组成部分,是一种重要的解题思想,对提高学生解题能力、提高教学质量有着至关重要的作用。在课堂教学中恰当地运用化归思想,可提高学生的学习效率,提升课堂的教学效率,帮助学生更好地解决问题。
(责编 吴美玲)

