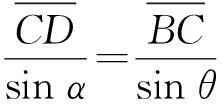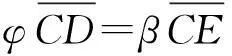单球面折射成像公式及其应用
张家乐 王化银
(淮北市第一中学 安徽 淮北 235000)

单球面折射成像公式及其应用
张家乐王化银
(淮北市第一中学安徽 淮北235000)
摘 要:物理竞赛几何光学球面折射问题的求解,直接利用单球面折射成像公式,往往能使得求解过程快速而简洁.
关键词:几何光学球面折射物理竞赛
单球面折射问题在竞赛试题中时常出现,参考解法中用到的式子较多,且进行了较多的近似处理,学生不易理解.若直接利用球面介质对光线折射的普通规律——单球面折射成像公式,则能使得求解过程快速而简洁.
1公式推导
如图1,设其中折射球面的球心为C,球面两侧介质的折射率分别为n1和n2,且n1 图1 由于i1和i2都很小,故由近似关系应有sini1=i1,sini2=i2,则上式变为 n1i1=n2i2 又由图中的几何关系可以看到i1=α+θ和i2=α-β,代入上式便为 以h表示图中B点到主光轴的距离,R表示球面半径,则由小角的近似关系可以得到 代入上式并整理可得 上式即为单球面折射时的物像距公式,式中各物理量的正、负取值有一定的规则,这一规则是:入射光线从左方射来时,球心在界面的右侧,则R取正值,球心在界面左侧,则R取负值;实物和实像的物距和像距都取正值;虚物和虚像的物距和像距都取负值. 2竞赛试题解答 2.1题目1 【例1】(第32届全国中学生物理竞赛预赛第16题)如图2所示,一垂直放置的高为15.0 cm的圆柱形中空玻璃容器,其底部玻璃较厚,底部顶点A点到容器底平面中心B点的距离为8.0 cm,底部上沿为一凸起的球冠,球心C点在A点正下方,球的半径为1.75 cm.已知空气和容器玻璃的折射率分别是n0=1.0和n1=1.56.只考虑近轴光线成像.已知:当λ≪1时,sinλ≈λ. (1)当容器内未装任何液体时,求从B点发出的光线通过平凸玻璃柱,在玻璃柱对称轴上所成的像的位置,并判断像的虚实; (2)当容器内装满折射率为1.30的液体时,求从B点发出的光线通过平凸玻璃柱的上表面折射后所成像点的位置,并判断这个像的虚实. 图2 2.1.1原解答 (1)容器底部凸面两侧介质的折射率分别是n1=1.56和n0=1.0.如图3,由B点发出的经过球心C的光线BA经过顶点A后,方向不变,进入空气中;由B点发出的与BA成α角的另一条光线BD在D点折射,设折射角为φ,并与前一条出射光线交于E点,E点即B点的像点的位置. 图3 由折射定律和几何关系得 n1sinθ=n0sinφ (1) γ=α+θ (2) φ=γ+β (3) 在三角形BCD和三角形CDE中 ,由正弦定理可得 (4) (5) 由于只考虑近轴光线成像,所以α,β,θ,φ都是小角度,式(1)、(4)、(5)可写为 n1θ=n0φ (6) (7) (8) 由式(6)、(7)可得 所考虑的光线是会聚的,故所成的像为实像.由式(2)、(3)、(6)、(7)、(8)可得 将题给数据代入上式得 1.75 cm=9.75 cm (9) 由式(9)和题给数据得 (8.0-1.75+9.75) cm=16.0 cm (10) B点发出的光线通过平凸玻璃柱,在玻璃柱对称轴上所成的像点的位置在C点正上方9.75 cm处或在B点正上方16.0 cm处. (2)容器底部凸面两侧介质的折射率分别是 n1=1.56和n2=1.30.如图4,由B点发出的经过球心C的光线BA经过顶点A后,方向不变,进入液体中;由B点发出的与BA成α角的另一条光线BD在D点折射,设折射角为φ,并与前一条出射光线交E点,E点即B点发出的光线第一次折射后所成像点的位置. 图4 由折射定律和几何关系可得 n1sinθ=n2sinφ (11) γ=α+θ (12) γ=φ+β (13) 在三角形BCD和三角形CDE中 ,由正弦定理可得 (14) (15) 由于只考虑近轴光线成像,所以α,β,θ,φ都是小角度, 式(11)、(14)、(15)可写为 n1θ=n2φ (16) (17) (18) 由式(16)、(17)可得 所考虑的光线是发散的,故所成的像为虚像.由式(12)、(13)、(16)、(17)、(18)得 将有关数据代入上式可得 1.75 cm=26.25 cm (19) 由式(19)和题给数据得 (1.75+26.25-8.0) cm=20.0 cm (20) B点发出的光线通过平凸玻璃柱,第一次折射后所成的像点的位置在C点正下方26.25 cm处或在B点正下方20.0 cm处. 2.1.2利用单球折射成像公式解答 (1)当容器内未装任何液体时,根据单球面折射成像公式得 即 解得 v=8.0 cm 所成的像点的位置在A点正上方8.0 cm处,即B点正上方16.0 cm处. (2)当容器内装满折射率为1.30的液体时,根据单球面折射成像公式得 即 解得 v=-28.0 cm 所成的像点的位置在A点正下方28.0 cm处,即B点正下方20.0 cm处. 2.2题目2 【例2】(第25届全国中学生物理竞赛预赛第19题) 如图5所示,一细长的圆柱形均匀玻璃棒,其一个端面是平面(垂直于轴线),另一个端面是球面,球心位于轴线上.现有一根很细的光束沿平行于轴线方向且很靠近轴线入射.当光从平端面射入棒内时,光线从另一端面射出后与轴线的交点到球面的距离为a;当光线从球形端面射入棒内时,光线在棒内与轴线的交点到球面的距离为b.试近似地求出玻璃的折射率n. 图5 2.2.1原解答 入射的两条光线如图6所示.α1和β1是从平端面入射的光线通过球形端面时的入射角和折射角;α2和β2是从球形端面入射的光线通过球面时的入射角和折射角.根据折射定律有 nsinα1=sinβ1 (21) sinα2=nsinβ2 (22) 图6 由几何关系有 β1=α1+δ1 (23) β2=α2+δ2 (24) 设球面的半径为R,注意到α1,α2,δ1,δ2都是小角度,故有 Rα1=aδ1 (25) Rα2=aδ2 (26) 根据题给的条件,式(1)、(2)可近似表示成 nα1=β1 (27) α2=nβ2 (28) 由式(3)~(8)得 (29) 2.2.2利用单球折射成像公式解答 根据单球面折射成像公式得 当光从平端面射入棒内时 当光线从球形端面射入棒内时 解以上两式得 竞赛试题的原解答,相当于将单球面折射成像公式从头至尾又推导了一遍,其中涉及到折射定律、几何关系及近轴光线情况下近似处理,过程呈现中用到的式子也必然较多.但这种解法辅助以光路图,成像位置、虚实,一目了然,较为直观.直接利用单球面折射成像公式求解此类问题,省去了中间推导的繁杂过程,简洁、明了,像的虚实也可以根据像距v的正负进行判断.对于高强度的物理竞赛拔尖选优考试,后一种方法更为高效、省时,同时也能反映出学生对物理钻研的深度与广度. 参 考 文 献 1程稼夫.中学奥林匹克竞赛物理讲座.合肥:中国科学技术大学出版社,2000 (收稿日期:2015-10-17)