以问题为主线的高三物理一轮复习——以“圆周运动”一节为例



以问题为主线的高三物理一轮复习——以“圆周运动”一节为例

帅厚梅

(扬州市新华中学江苏 扬州225009)

以问题为主线的复习就是指教师在课堂上创设问题情境，以环环相扣的问题形式引导学生进行复习．这种复习方式让学生自己通过思考、讨论、交流，寻求解决问题的方案，而不是被动接受教师现成的知识结论，这样能够唤醒学生的问题意识，从而培养学生分析问题和解决问题的能力．下面就以一轮复习“圆周运动”一节为例加以说明．

1以问题为主线梳理基本知识——通过例题“学以致用”

在梳理知识环节中针对不同知识点设有不同问题，并根据知识点的抽象程度、重要程度等及时通过典型例题进行补充说明．设有如下问题：

匀速圆周运动中的“匀”字是指什么物理量不变？

描述匀速圆周运动运动快慢的物理量有哪些呢？

线速度、角速度、周期、频率、转速是如何定义的？符号是什么？单位是什么？

频率和周期有什么关系？频率和转速有什么不同？

若物体做圆周运动的时间取一个周期，则线速度、角速度的定义式如何改写？线速度、角速度用频率如何表示？

线速度与角速度之间有什么关系？

向心加速度的物理意义是什么？向心加速度的常用表达式有哪些？向心力的常用表达式有哪些？

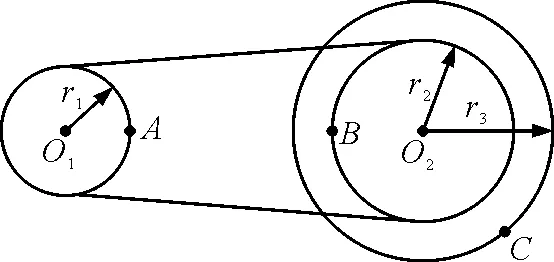
图1　皮带传递装置示意图

【例题】如图1所示，O1为皮带传动装置的主动轮的轴心，轮的半径为r1，O2为从动轮的轴心，轮的半径为r2，r3为与从动轮固定在一起的大轮的半径．已知r2=1.5r1，r3=2r1．A，B，C分别是3个轮边缘上的点，那么质点A，B，C的线速度、角速度、周期以及向心加速度之比分别是多少？

这一典型例题中的问题“质点A，B，C的线速度、角速度、周期之比是多少？”，是在复习完“线速度、角速度、周期”3个概念后提出的；而“质点A，B，C的向心加速度之比是多少？”，则是在复习完“向心加速度”概念后追加提出的．这样“一题多用”，充分挖掘一道题目的价值，可以避免重复审题，节约课堂时间，从而提高课堂效率．在典型例题的环节中，也并不是由教师从头讲到尾，而是让学生讨论交流，自主寻找解决问题的方案．

2以问题为主线掌握基本模型——通过变式“由浅入深”

在掌握基本模型这一环节中，为了更好地衔接各部分内容，这里将典型例题和变式训练都以“环环相扣的问题”呈现，让学生在“不知不觉”中“拾级而上”，由浅入深地掌握相关知识，训练学生思维的深度．

图2

(1)圆桶模型

如图2所示，设有如下层层问题：

物体随圆桶做匀速圆周运动，受哪些力的作用？

谁来提供物体做匀速圆周运动的向心力？

欲使物体与圆桶保持相对静止，对圆桶转动的角速度有什么要求？

(2)圆锥筒模型

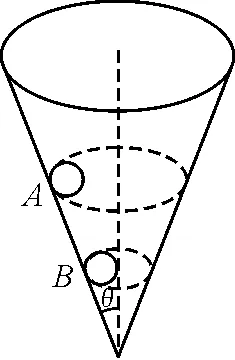
图3

如图3所示，圆锥筒内壁光滑．设有如下层层问题：

小球A在圆锥筒中做匀速圆周运动，受哪些力的作用？向心力由谁来提供？向心力方程如何书写？

若有A和B两相同的小球在圆锥筒中不同高度做匀速圆周运动，那么两者转动的线速度、角速度、周期、向心加速度以及所受弹力的大小关系如何？

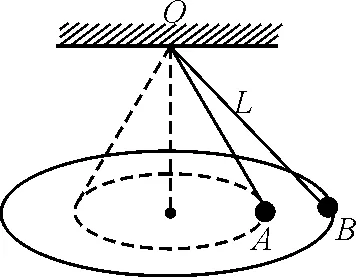
图4

(3)圆锥摆模型

如图4所示，有如下层层问题：

小球A在细线作用下做匀速圆周运动，受哪些力的作用？向心力由谁来提供？向心力方程如何书写？

若有A和B两相同的小球在同一水平面上做匀速圆周运动，那么两者转动的线速度、角速度、周期、向心加速度以及所受拉力的大小关系如何？

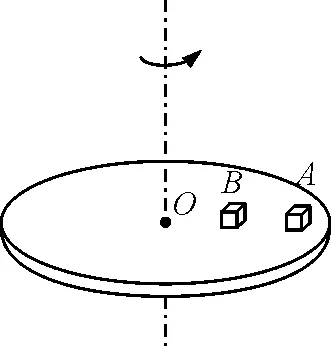
图5

(4)圆盘模型

如图5所示，有如下层层问题：

物体A放在圆盘上随圆盘一起做匀速圆周运动，受哪些力的作用？向心力由谁来提供？向心力方程如何书写？

欲使物体与圆盘保持相对静止，对圆盘转动的角速度有什么要求？

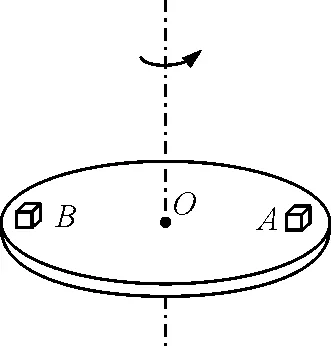
图6

若有A和B两相同物体放在圆盘上随圆盘一起转动，两物体与圆盘间的动摩擦因数相同，随着圆盘角速度的增加，哪个物体先发生滑动？

如图6所示，若A的质量为m，B的质量为2m，到圆心的距离相同，两物体与圆盘间的动摩擦因数相同，则随着圆盘角速度的增加，哪个物体先发生滑动？

如图7所示，A，B，C3个物体放在圆盘上随圆

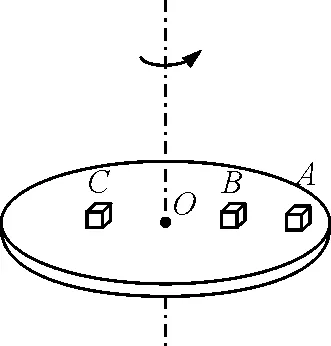
图7

盘一起转动，A离轴的距离是2R，B和C离轴的距离为R，A和B的质量均为m，C的质量为2m，它们与圆盘的最大静摩擦因数相同，则随着圆盘角速度的增加，哪个物体先发生滑动？

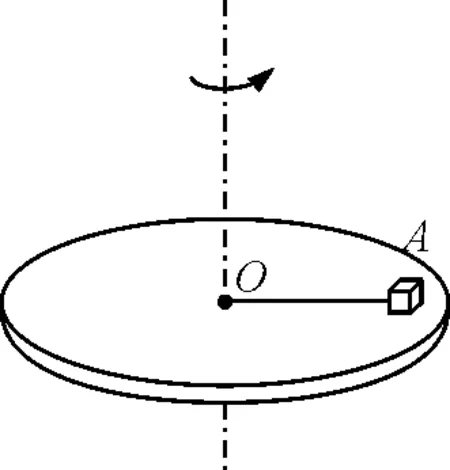
图8

如图8所示，若物体A用一根绳子拴在圆心，随圆盘一起转动，那么物体A需要的向心力谁来提供？

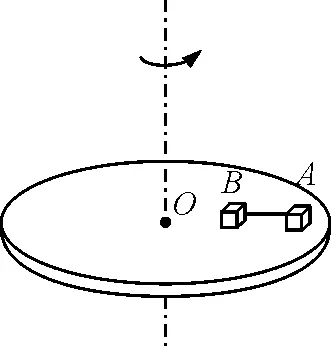
图9

如图9所示，A与B两相同物体用绳子相连放在圆盘上，随圆盘一起转动，当圆盘的角速度为多少时，绳子上开始产生拉力？

设A离轴的距离为2R，B离轴的距离是R，欲使A和B两物体都与盘保持相对静止，圆盘转动的最大角速度为多少？此时剪断绳子，A和B两物体分别做什么运动？

3以问题为主线学会基本方法——通过小结“触类旁通”

爱因斯坦说过，“什么是教育，当你把受过的教育都忘了，剩下的就是教育．”教师引导学生分析题目的目的不是让学生记住这些题目，题目本身学生很快就会忘记，那么“剩下的是什么”，剩下的就是分析这些题目的思路和方法，以及暗含其中的思维方式．所以在完成基本知识和基本模型的学习之后，笔者通过问题引导学生对本节课进行小结，重在掌握解题思路和方法．设有如下问题：

本节课你学习了哪些基本知识、基本模型？

解决圆周运动问题的基本方法是什么？核心方程是什么？

在整个教学过程中，教师创设问题情境，带着问题引导学生进行探究；学生交流合作、积极思考、大胆表达、敢于质疑，通过“问题对话”可以有效促进学生的发展．

(收稿日期：2015-06-30)