把教材缺陷当作一种资源来开发

☉甘肃省西和县稍峪中学　吕　强



把教材缺陷当作一种资源来开发

☉甘肃省西和县稍峪中学吕强

教材，用于教学活动的材料，是教学内容的主要载体.在课程资源中教材是必不可少的重要资源之一，教科书又是教材的核心资源.

《国家基础教育课程改革指导纲要》明确提出了教师应有效开发课程资源组织教学的要求，并且高度概括了这种开发与利用的特点应是“灵活的”、“创造性的”.任何教材到了学校，到了师生手中，都应有一个再加工、再创造的问题，即校本化、生本化的问题，也就是将其内化的问题.最好的教材应该是国家、地方和校本三种教材通过师生创造的“三合一”教材，这样内化了的教材沿袭了国家教材的神韵，接通了地气，又融入校本特色.不开发教材的潜在资源，不挖掘师生的潜能，教材何以内化？怎能“用教材教”出创意呢？

一线教师对教材应该持怎样的态度呢？百分之百的接纳不可取，完全信服甚至迷信教材也是不可取的.相信而不迷信、评判融入传承才是正态.因为对教材保持扬弃态度与立场，所以我们发现了人教版初中数学教材的一些问题与缺陷，虽然它们不是教材的致命“病垢”，但也如同一碗香喷喷米饭里吃出了一粒沙子，难免影响人的食欲.我们一线教师是教材的使用者与实践者，使用教材并对使用情况进行研究，能对教材提出宝贵的意见，反馈意见与建议，使教材更完善.下面通过几个典型案例来分析人教版初中教科书微调整、微变化与微更新的渊源.

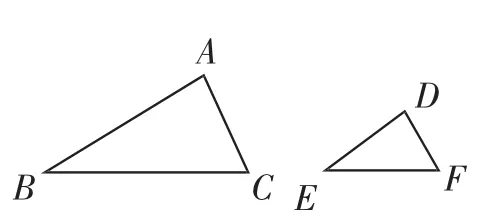
图1

案例1人教版（2004年审定）数学九年级下册第二十七章“相似”第2节“相似三角形的周长和面积”中的例6：如图1，在△ABC和△DEF中，AB=2DE，AC=2DF，∠A= ∠D，△ABC的周长是24，面积是48，求△DEF的周长和面积.

教材缺陷：周长是24，面积是48的△ABC不存在.在这个综合性问题中，相似三角形的判定和性质是问题中的显性关系，三角形的面积与周长的关系是隐性关系，忽视此隐性关系，正是教材缺陷之所在.

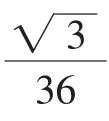
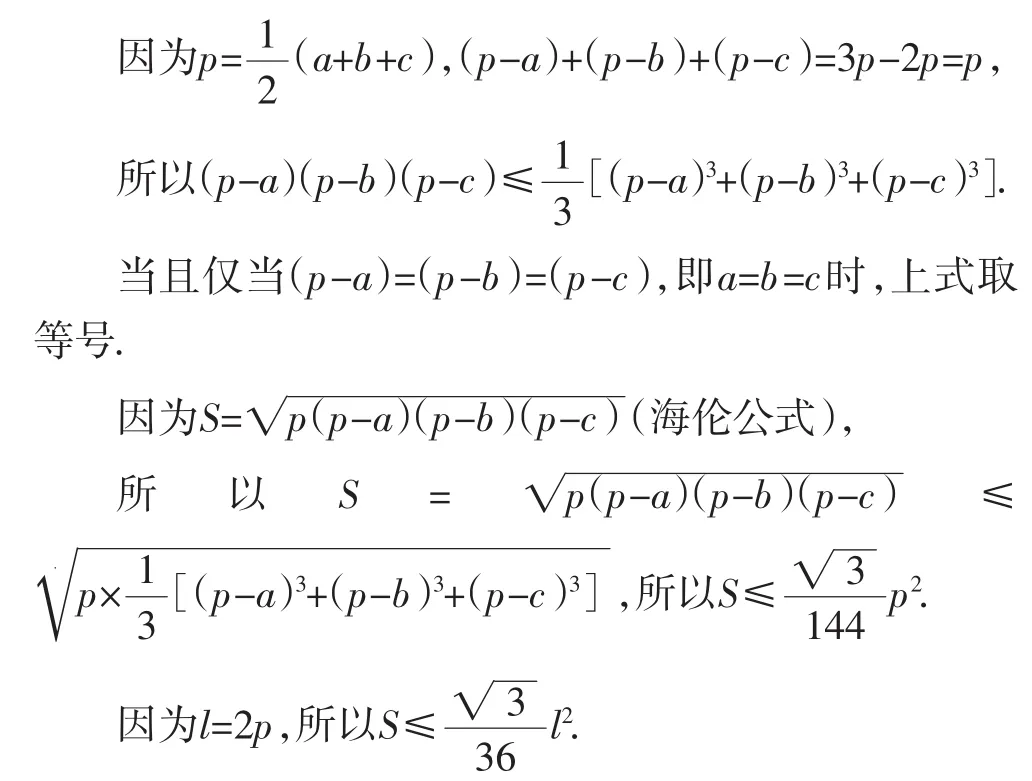
（1）公式①的推导.

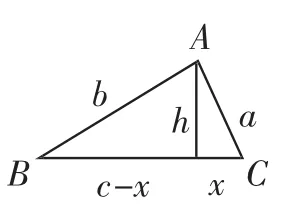
图2

证明：如图2，设h是△ABC的底边c上的高，根据勾股定理，得

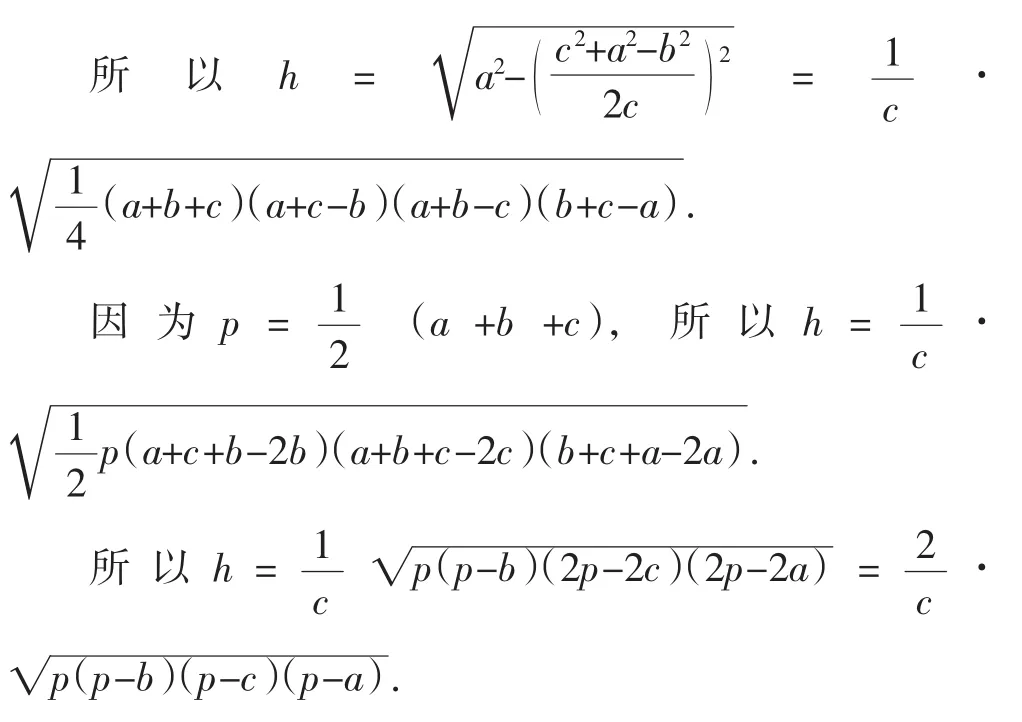
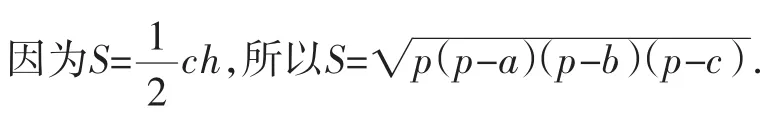
（2）公式②的推导.

由该不等式易知，周长一定的三角形，以等边三角形的面积最大；面积一定的三角形，以等边三角形的周长最小.

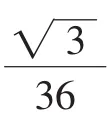
教材回顾：人教版教科书修订改版时，此例改为：如图1，在△ABC和△DEF中，AB=2DE，AC=2DF，∠A=∠D，△ABC的周长是24，面积是求△DEF的周长和面积（见人教版（2013年教育部审定）九年级数学下册第52页）.从而彻底消除了此处的教材缺陷.

案例2义务教育教科书（2004年审定）人教版数学八年级上册第37页的第7题：平面内两条相交直线是轴对称图形吗？如果是，它有几条对称轴？画画看.

教材缺陷：平面内两条相交直线的对称轴有两条.

资源开发：这个问题很简单，简单得无需思考，你就能直呼答案：两条.真的是两条吗？以前从没人质疑过.在数学课上，我们班的学生却给出了另外一个答案——四条，这是任何教参上没有的结论.原来所有的人都用“静”的眼光看这个问题，或者说是凭直觉作出的判断.而我们班的学生是用“动”的眼光来看问题的，他们画了两条相交直线，让一条静止，让另一条旋转，两条直线的相交将呈现特殊的相交——垂直和不垂直的一般相交两种状况，依次对应着四条和两条对称轴（该问题亦用分类讨论的数学思想，分“特殊”和“一般”两种情况来处理）.这是以前任何书籍上都没有的正确结论，一道能有效培养学生思维品质的好题就这样被埋没了若干年，被“误解”了若干年.从教材出发，学生通过自主学习和合作探究，得出“未被前人发现”的正确结论.这就是“创新”，这样就是用“活”教材.

教材回顾人教版教科书修订改版时，将此题修改为：平面内不垂直的两条相交直线是对称轴吗？如果是，它有几条对称轴（见2013年审定人教版八年级数学下册65页）？缺陷彻底消除了，但问题的探究价值大打折扣.

案例3义务教育教科书（2013年审定）人教版数学八年级上册的第17页第7题：如图3，B处在A处的南偏西45°方向，C处在A处的南偏东15°方向，C处在B处的北偏东80°方向，求∠ACB的度数.

教材缺陷：“B处在A处的南偏西45°方向”这一条件是多余的.

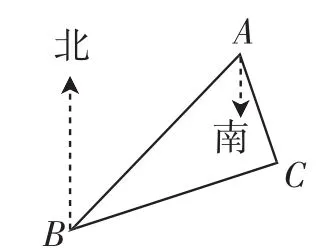
图3

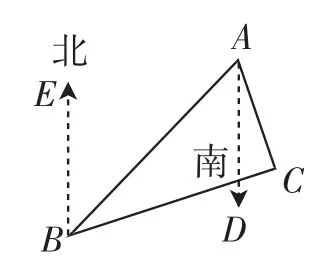
图4

资源开发：教学用书的解法思路为：

如图4，因为BE∥DA，

所以∠EBA=∠DAB=45°.

又因为∠ABC=80°-45°=35°，

且∠BAC=45°+15°=60°，

所以∠ACB=180°-∠BAC+∠ABC=180°-60°-35°= 85°.

解法1：如图4，设AD交BC于点D，

因为BE∥DA，所以∠EBC+∠BDA=180°.

又因为∠EBC=80°，

所以∠BDA=180°-∠EBC=180°-80°=100°.

因为∠BDA=∠ACB+∠DAC，∠DAC=15°，

所以∠ACB=∠BDA-∠DAC=100°-15°=85°.

点评：利用“两直线平行同旁内角互补”和“三角形的任意一个外角等于与它不相邻两个内角和”求解.

解法2：如图4，设AD交BC于点D，

因为BE∥DA，∠EBC=80°，

所以∠ADC=∠EBC=80°.

因为∠ACB+∠DAC+∠ADC=180°，∠DAC=15°，

所以∠ACB=180°-∠DAC-∠ADC=180°-15°-80°= 85°.

点评：利用“两直线平行同位角相等”和“三角形内角和定理”求解，还可利用“两直线平行内错角相等”、对顶角的性质和“三角形内角和定理”求解（解题过程略）.

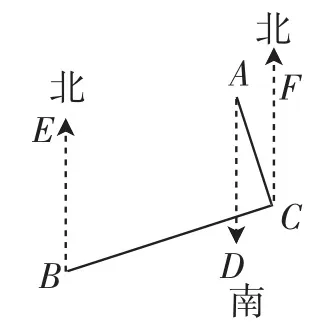
图5

解法3：如图5，过点C作CF∥DA，

则∠FCA=∠DAC=15°.

因为BE∥DA，CF∥DA，

所以BE∥CF.

所以∠EBC+∠BCF=180°.

因为∠BCF=∠ACB+∠FCA，

所以∠EBC+∠ACB+∠FCA=180°.

所以∠ACB=180°-∠EBC-∠FCA=180°-80°-15°= 85°.

点评：仅利用“平行线的性质”求解.

纵观“解法1”、“解法2”和“解法3”的整个解题过程，根本没有用到“∠DAB=45°（即B处在A处的南偏西45°方向）”，正是这三种解法揭示了“B处在A处的南偏西45°方向”这一条件是多余的，所以原题可将其去掉.

教材回顾：“B处在A处的南偏西45°方向”这个多余的条件，仍然留在教科书中.

案例4在过去随着探究性学习兴起，人教版初中数学教科书与时俱进，把“探究活动”作为专题或课题植入教材，让人耳目一新.比如人教版（2001年审定）九年义务教育三年制初级中学代数第二册96页“探究活动：a=bc型数量关系”，这节是被人教版删除的内容却给我们留下非常深刻的印象，它的引例选取了一个源于生活的实际问题，这个问题本身就是很好的教材与学材.如此精致的教材编排，可谓精益求精.下面我们回顾这节的引例“讨论一个实际问题”：有一大捆粗细均匀的电线，现要确定其总长度的值，怎样做比较简便（使用的工具不限，可以从中先取一小段作为检验样品）？

（教科书中）提示：由于电线的粗细是均匀分布的，所以每段同样长度的电线的质量也是相同，想一想，电线的总质量a、总长度b和单位长度c之间有什么数量关系.

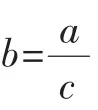
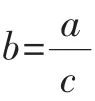
资源开发：在教学中，教师可引导和鼓励学生对本引例展开讨论，得出通过两次测量质量的方法确定电线总长度的种种方案，并归纳如下：

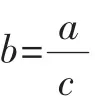
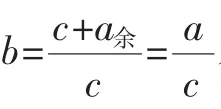
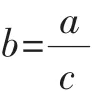
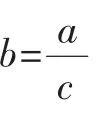
此后，教师可总结：以上我们从不同的角度讨论了确定电线（或电缆线）总长度的方法，引出a=bc型数量关系；现在，我们从不同的角度讨论a=bc型数量关系（引例教学完毕，探究性活动继续展开）.

教材回顾：人教版教科书修订改版时，删除了这节探究性活动，其引例也退出了教科书.一个具有探究价值的引例，只因教科书所给参考答案的失误，使其从教科书中消失了，真是“一只老鼠带害一锅饭”.

通过以上四个案例的探究，我们不难发现：如果教师把教材资源缺陷当作一种资源来开发，教材资源缺陷就会成为一种教育教学资源.其实，有些问题的解决不是缺乏资源，而是缺乏对资源进行开发的思考，而资源往往就是从人的头脑里“开发”出来的.

参考文献：

1.吕强，吕建科.对两道课本例题的再探讨［J］.中小学数学（初中版），2009（10）.

2.吕强.开发教材的隐性资源例说［N］.中国教师报，2011-12-07（16）.

3.吕强，石芳雄.一道课本例题是错题［J］.中学生数学（初中版），2010（12）.

4.吕强，杜仲雄.一道课本习题可以简化［J］.中学生数学（初中版），2011（11）.

5.吕强，邵曙.对一个引例的教学建议［J］.中小学数学（初中版），2005（1）.