搭建支架，步步登高*——基于整体建构的基本作图资源整合教学

☉山东省滨州市北镇中学初中部　邢成云



搭建支架，步步登高*——基于整体建构的基本作图资源整合教学

☉山东省滨州市北镇中学初中部邢成云

*本文系山东省教学研究课题《全息教学论下的跨越式教学》（课题编号：pt-20120126）的延伸研究成果之一：基于资源整合教学的课堂设计.主持人：邢成云.

一、写在前面

五种尺规基本作图（除了最基本的作线段）分散于（人教版）教材的各个部分，跨越2章的空间，这种编排不利于培养学生的基本作图技能，也不利于学生发散思维的培养.作一个角等于已知角的作图是在八年级上册第12章第37-38页12.2的例1之后安排的；八年级上册第12 章12.3一节第48页的第一个思考之后，安排了角的平分线的作法；在八年级上册第14章3.1.2的第62页，通过例1安排了过直线外一点作已知直线的垂线的作图；同一节通过例2安排了线段的垂直平分线的作图.其顺序是：作已知角→作已知角的平分线→过直线外一点作已知直线的垂线→作线段的垂直平分线.其中作垂线中的“过直线上的一点”安置在习题中，而这正是从角平分线到垂线作图的引桥.通过各类作图之间关联的分析，笔者把这些基本作图汇聚于连续的2节课内，先期的作图不限制工具，当把全等三角形、轴对称两章知识完成后，集中安排了尺规作图的学习.

本节以第一节基本作图课（即完成了“作线段等于已知线段；作角等于已知角；作角的平分线”三类作图的学习）为基，形成支架，然后循级而上，完善五种基本作图，其中过直线上一点作垂线等价于作平角的角平分线，这就是本节课的逻辑起点，而后通过化归将其他类型的作图不断转化，直至完成基本作图的整体模块.

二、教学目标

（1）以角的平分线为先行组织者，探寻“过直线上一点作直线的垂线”的尺规作图，继而完成“线段的中垂线”“过直线外一点作直线的垂线”的尺规作图，厘清逻辑顺序；

（2）集中再现五种基本图形的基本画法，熟练掌握其技法，正确理解它们的作图原理，在实际问题中能简单地应用.

三、教学准备

每位同学准备一张练习纸，上有一个钝角∠α（课始作图用）和一个△ABC（以备后面的练习用）.

四、教学过程

1.抓生长点，特殊中筑起支架

设计说明：点与直线有两种位置关系：点在直线上、点在直线外，其中点在直线上是本节课三个作图的基点，过直线上一点作垂线，无非是揭示一般中的特殊，去作以那一点为顶点的平角的角平分线所在直线，这是学生已有的技能，这个根基稳了，其他两类作图的支架就搭建起来了！

师：到现在为止，基本的尺规作图已经完成了哪些？

生：已经学会了三个：作线段等于已知线段；作角等于已知角；作角的平分线.

师：是的，我们步步推进，已经完成了三个基本作图，请同学们打开练习纸，用尺规作∠AOB=∠α，并作出它的角平分线.

（生作图中）

（待学生完成后，用几何画板演示）师：同学们思考下面的问题：若通过直线上一点作这条直线的垂线，该如何实施？请同学们先画出已知图观察，看谁最先破解这个问题.

（生思考中）

生1：我知道.

（师示意生1先不要急于发言，给其他同学思考的机会）

（师巡视中发现有一半以上的同学把思路想出来了，遂示意生1发言）

生1：从图上看就是一个特殊的角——平角，把平角平分不就出现垂线了吗？所以我作了平角的角平分线，再反向延长.

师：其他同学的思路怎样？

生2：和生1思路一样，就这么想的.

师：哦，很好，说明同学们善于利用已知处理未知问题，这在数学上叫什么？

生众：化归.

师：是的，这就是“化归”的作用，把过直线上一点作直线的垂线问题转化为作平角的角平分线问题.

（接着，师用几何画板展示：先测量钝角，然后拉伸，其中有一个状态即为平角状态，发现此时的角平分线恰好与平角形成的直线垂直）

作法归纳（图1）：

（1）以C为圆心，适当长为半径画弧，交直线AB于点E、F；

图1

（3）画直线CD，直线CD即为所求.

2.拾级而上，开放中发现方法

设计意图：只要把直线AB上的线段EF分离出来，立即就会发现CD就是线段EF的垂直平分线，因此，笔者通过问题引领，启导学生观察后发现图中蕴含着EF的垂直平分线，然后诱导学生发现其作法，这个作法就是基于以前的经验，当然离不开垂直平分线性质定理的逆定理的助力.

师：请同学们观察图1，你能发现这个图中有哪些正确的结论？

生3：C为线段EF的中点，CD是线段EF的垂直平分线.

生4：若连接DE、DF，则△DEF为等腰三角形，满足“三线合一”.

师：两位同学说的都很好，谁还有说法？

生众：没有了.

师：就现在研究的问题，请同学们大胆设想一下，我们下一步要干什么？

生5：作一条线段的垂直平分线.

师：对，会作吗？从图1能获得启示吗？请同学们思考.

生6：在这里，线段的中点不知道，因此，要作线段EF的垂直平分线，根据判定方法及前面的经验，需要D那样的点两个，所以再找出另外一个类似的点就行了.

师：分析的非常透彻，这样一来，剩下的任务就是找出那个类似的点，该怎么找？

生6：重复点D的找法就行.

生7：不需要，一次性画弧就行了，在线段的上下两方分别画弧，两弧就会有上下两个交点，然后通过这两点作直线即可.

师：请同学们判断一下，作法是否合理？

生众：合理不合理需要证明.

师：说得好，说明同学们有了很强的规则意识，不是看当然、想当然了，谁来说明？

生8：根据画法，结合垂直平分线定理的逆定理，D点到线段EF两端的距离相等，说明点D在线段EF的垂直平分线上，同理，另外一点也在线段EF的垂直平分线上，根据两点确定一条直线可证.

师：推理充分、得体，说明这个方法可行，同学们明白这回事吗？

生众：明白.

师：请同学们作线段AB的垂直平分线，并梳理其作法.

已知：线段AB.

求作：线段AB的中垂线.

作法（图2）：

图2

（2）过C、D两点作直线.

直线CD即为所求.

3.用好支架，迁移中破解难点

设计意图：过直线外一点作直线的垂线，这是尺规作图的至高点，也是难点，同时也是整节课的难点所在.通过引领学生反观图1和图2，发现其中垂直的端倪，探寻出其核心在于“与直线相交的那条弧”，有了这个支架，前文的作图之法就容易发生迁移，将难点化解.

师：过直线上的点作直线的垂线及线段的中垂线的作法解决了，还剩下哪一类问题需要解决？

生9：过直线外一点作直线的垂线.

师：是的，还有点在直线外这一类情况，试试看，你会作吗？

生10：先通过直线外一点作已知直线的平行线.

师（追问）：平行线！怎么作？

生10：过这一点先任意作一直线与已知直线相交，然后以这一点为顶点作等于两直线夹角的同位角.

师（作惊讶状）：哇，这样一来这一条直线就是原来那一直线的平行线了，我们岂不是顺便发现了“过直线外一点作已知直线的平行线”这一个新的作图吗？这真是“得来全不费工夫”啊！

（学生自发的掌声）

师（追问）：再怎样操作呢？

生10：接下来就是重复过直线上一点作直线的垂线的作法了.

师（面向全体追问）：这样可以吗？

生众：哦，可以！

师：为什么？

生众：通过平行线的性质“同位角相等，两直线平行”可以证明.

点评：出乎老师的预设，没想到学生来了这么一招，纵然这一方法比较复杂，需要作“平行线”当助力，但这是学生鲜活的思路，字字句句流泻出思维的灵动、散发出化归的魅力，无意中捡拾到两颗美丽的珍珠！

师：这位同学充分利用了数学上的核心思想——化归，把这一问题转化成已经解决的问题来处理，值得我们学习！同学们先梳理一下这个方法，并揣摩其中的道理.

（生梳理中）

师：接下来，请同学们借助图1、图2继续思考，除了这一方法，谁还有其他方法？

（生沉默）

师：我们想一想刚才作垂直的方法，其关键在哪里？

（生思考中，陆续有三分之一的同学举手）

生11：找到与直线相交的那条弧.

师：噢，有了这条弧，问题就变成已经解决的问题了，可那条弧该怎么画？

生12：随便画就行.

生13：不能随便，随便画弧不一定能与已知直线相交.

生12：哦，对，需要能与直线相交.

师：能交只是一个定性认识，具体怎样操作？

生13：以直线外那一点为圆心，以大于这点到直线的距离的长为半径画弧.

生14：那样说还不确切，应该具体找一个点，让这个点与直线外那一点分居直线两旁，就能保证交点的存在了.

（生众认可）

师：生14的想法很好，比较具体，能详细表述一下吗？

生14：在直线AB另一侧任取一点K，以点C为圆心，以CK为半径画弧，交直线AB于点D、E，然后按角平分线的作法操作就行.

师：好，表达清晰，下面我们一起归纳一下这一作法.

已知：直线AB和AB外一点C.

求作：AB的垂线，使它经过点C.作法（图3）：

（1）任意取一点K，使K和C在AB的两旁；

（2）以C为圆心，CK的长为半径作弧，交AB于点D和E；

图3

（4）作直线CF.

则直线CF就是所求的垂线.

4.一图“三线”，应用中突出核心

设计意图：通过尺规作三角形的“三线段”，把五类作图中的三种核心作图全盘托出，既是对作图的技法的巩固，又是对三角形三线段的再认识，形成基本尺规作图与概念的对接，明确高线是通过三角形的一个顶点向对边作垂线而获得的，是过直线外一点作垂线的应用；中线则通过作线段的中垂线先获得中点，再与所对顶点连接而成，显然是中垂线作图的应用；角平分线就是地地道道的角平分线作图.在实战中见证学生的技法，同时通过口述作法锻炼学生的语言转换技能，和谐学生的动口、动手、动脑，一举多得.

练习：如图4的△ABC，用尺规分别作出BC边上的高、∠B的平分线、AB边的中线，保留作图痕迹并口述作法.（说明：作法口述，需要同桌之间相互检查）

图4

学生利用练习纸独立完成，笔者巡视、指点，整体完成不错，有一小部分作高线有障碍，通过笔者和部分同学的帮扶基本达标.

（私下交流较多，限于篇幅，在此从略）

5.原理探寻，交流中建构体系

设计意图：通过学生再次梳理与反思，环环相扣、一脉相承的五类基本作图，自然可以凝聚成一个尺规作图的群体，这个群体的携手发力就可以解决相对复杂的作图问题，为几何学习开拓市场，为几何由静返动提供了可感的操作，力图实现小结的点睛之用和凝聚之力.同时通过原理探寻，明确几何原理，“知其然”的同时“知其所以然”，这样作图的根、脉、原理就厘得清清楚楚了.

师：至此，五种基本作图基本达成！反躬自问，自己是否明白了作图的方法及原理，它们之间是怎样关联的？请同学们理出一条线索把5种作图归纳，可相互补充.

生15：整个作图就是一个不断转化的过程.

师：是的，转化是整节课的命脉，通过转化让我们不断走向成功.

生16：截线段在每一个作图中都有体现，我从作角等于已知角开始，再作这个角的角平分线，借助角平分线的作法，过直线上一点作直线的垂线，顺接思路，作线段的垂直平分线，进一步过直线外一点作直线的垂线.

师：这是我们学习基本作图的基本线索，表述的条理清晰，很好！我再提几个问题请大家思考.作一个角等于已知角，用的是什么几何原理？

生17：全等三角形的对应角相等.

师：你通过什么方法判断它们全等？

生17：SSS.

师：作角的角平分线借助了什么原理？

生18：也是全等三角形的对应角相等.

师：通过什么方法判断它们全等？

生18：也是SSS.

师：“过直线上一点作已知直线的垂线”的方法源于哪类作图？

生19：就相当于作一个平角的平分线.

师：是的，通过“作一个角的平分线”的尺规作图的支架作用，我们得出了“过直线上一点作已知直线的垂线”的方法.作线段的垂直平分线呢？

生20：这个复杂，可先分别连接图2中的AC、BC、AD、BD，通过SSS证△ACD与△BCD全等，得∠ACD= ∠BCD，再证AB上的两个小三角形全等即可.

生21：不用再证全等，直接说明DC是∠ACB的角平分线，用三线合一就行了.

生22：一个全等也不需要证，直接利用线段垂直平分线性质的逆定理就行，C、D两点都在AB的中垂线上，根据两点确定一条直线，CD当然就是AB的中垂线了！

（生22说完，有掌声）

师：是的，三种方法都可行，但最简单的还是生22的做法，我们面对一个问题既要发散思维，又要注意优化选择思路.过直线外一点作直线的垂线呢？

生众：证明思路和中垂线的一样.

师：同学们一眼就看穿了，是的，观察图3可以看出思路与中垂线的证明一致.这样一来，前面每一个作图法的合情默认，其合理性在同学们的交流中得到了逻辑认证，现在我们心里踏实了，下一节我们将共同关注作图在现实生活中的应用！

6.分层作业，保底中关注差异

必做题：

（1）整理5种基本作图，写出画法，并体会每一个作图之间的联系.

（2）如图5，已知点M、N和∠AOB，求作一点P，使P到点M、N的距离相等，且到∠AOB的两边的距离相等.

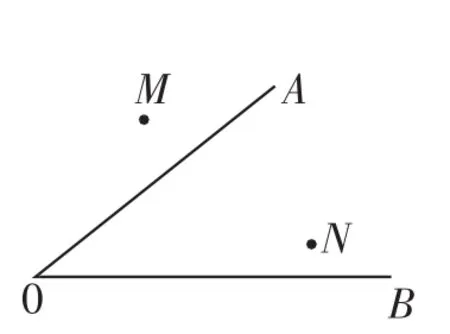
图5

选做题：

如图6，Rt△ABC中，∠ACB = 90°，∠CAB=30°，用圆规和直尺作图，用两种以上方法把它分成两个三角形，且要求其中一个三角形是等腰三角形（保留作图痕迹，不要求写作法和证明）.

图6

设计说明：对于选做题，采用五种尺规作图中的作线段、作线段的垂直平分线、作角平分线、作角中任何一个基本作法都可以完成目标图形，搭建了让学生对每种基本作图一个思维发散的空间，是学生复习巩固和灵活体验五种基本作图方法的一个好题，但根据往年的经验，学生大都集中于画线段的中垂线和角平分线这两种方法，对其他方法熟视无睹，缺乏另外的作图意向，折射出对这五种作图法的熟练和功能理解不够深入，还停留在一种记忆意识与技术层面，没深入到理性的应用意识，存在着知识的应用盲点.一旦遇到像这类作法开放的作图题时，就会暴露出思路不开阔的弱点，因此，透视作图的渊源，熟练每种作图方法和澄澈作图原理，并适度增加作图应用的训练势在必行.

五、写在后面

基本作图的集中呈现，展现了五种作图之间的内在关联，打通了它们之间的横隔，让本来就是技能技法的教学内容，绽放出思想的花蕾、喷涌出思维的泉水.若我们停留在一招一式的技能上，纵然明其理，也弄不清来龙与去脉，彼此孤立，各自为战，会大大削弱数学的内在魅力，基于尺规的作图，把几何直观与逻辑推证拿捏在一起，展露了图形的鲜活与灵动，增添了数学的秀色、彰显出数学的本味！

参考文献：

1.邱海敏.在探索中提高——尺规作图复习课案例［J］.黑龙江教育·中学教学案例与研究，2008（10）.

2.吴瑞.对教学中尺规作图难点的突破［J］.中学时代，2012（22）.

3.肖霄.对初中阶段尺规作图教学的反思和建议［J］.中学数学教学，2012（4）.

4.朱木兰.基本作图［J］.中学数学教学，1995（3）.

5.张建鹏.从学生熟悉的材料开始尺规作图的教学［J］.数学教学通讯（教师版），2011（24）.