精选“数学现实”,践行“用教材教”——以七年级“余角与补角”教学为例
☉江苏省南通市通州区西亭初中 邵 艳
精选“数学现实”,践行“用教材教”——以七年级“余角与补角”教学为例
☉江苏省南通市通州区西亭初中邵艳
近读《中学数学》,严冬梅老师在文1中对专家教师李庾南老师“余角与补角”新授课的教学设计进行了解读和赏析,感受到专家教师辨识学段特征的功夫,同时在初中几何起始教学阶段就重视对学生的推理表达能力的训练,让笔者深受教益.恰好在最近一次教研活动中,笔者有机会执教七年级“余角与补角”新课,借鉴了上述课例中的很多观点和立意,研讨课取得较好的反响和好评.本文整理该课的教学设计,并整体阐释教学立意,与更多同行分享.
一、“余角与补角”教学设计
环节1:由一组习题引入定义
开课之初,在黑板上依次画出一条直线AB,在直线AB上取一点O,利用三角尺引射线OC使∠BOC为直角,再利用三角尺作出∠COD= 30°(如图1).

图1
问题1:图中除平角外,有几个角?如何表示?
问题2:图中有几个锐角?锐角的度数有什么关系?图中钝角的度数是多少?
预设意图:复习角的概念、表示法,并会利用平角、直角的关系求出其他角的度数.“问题2”为进一步定义互余、互补提供“数学现实”情境.
互余的定义:两个角的和等于90°,就说这两个角互为余角,简称互余.
讲解:如果∠1+∠2=90°,就可以说∠1是∠2的余角,或∠2是∠1的余角.如果两个角互余,把两个角粘在一起的话,就构成一个直角.如图2.

图2
互补的定义:如果两个角的和等于一平角(180°),就说这两个角互为补角,简称互补.

讲解:如图3,∠3+∠4=180°,所以∠3,∠4互为补角.∠3是∠4的补角,∠4也是∠3的补角.
注意:提醒互余、互补只是定义了两个角度之间的数量关系,与位置关系无关.但是一些具有特殊位置关系的角,如图1、图2、图4中的两角就同时具有互余或互补的性质.
环节2:一幅三角尺摆放出的互余、互补关系
过渡语:现在同学们都知道了一幅三角尺中两个锐角都是互余关系.下面让我们把一幅三角尺进行如下不同的摆放(图5~8),试分析α、β之间的关系.
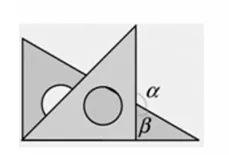
图5

图6

图7

图8
问题3:α与β一定相等的摆放方式有几种?
预设意图:图6、图7中α与β一定相等,这时追问学生推理依据.给学生写出规范的推理语句,并总结性质:同角(等角)的余(补)角相等.
问题4:你发现上述摆放方式中的α与β还有怎样的数量关系?
预设意图:让学生发现互补、互余两种关系.特别是图8中这种互余的关系,在后来的几何解题中有广泛的应用,这里需要让学生熟悉它们互余的道理,如何推证,写出简单的推理语句是这里训练的重点.
环节3:画图探究“双角平分线”基本图形及性质

图9
画图:如图9,画∠AOB=90°,在其内部引射线OC,再用量角器作射线OM、ON,使OM平分∠AOC、ON平分∠BOC.
安排学生度量∠MON的度数并小组内核对度量结果,思考∠MON的度数与∠AOB的度数有何关系?
预设意图:这是一个经典问题,与之前学生在线段双中点问题中积累下来的解答经验类似,需要学会洞察这类问题的深层结构,并学会推证结论.
环节4:课堂小结,当堂检测
引导学生小结本课所学互余、互补的概念和性质之后,进行5分钟的限时检测.
二、教学立意的整体阐释
1.精选数学现实,贴近学生最近发展区引入新课
《义务教育数学课程标准(2011年版)》倡导数学情境包括生活现实、数学现实及其他学科现实,对于初中几何教学来说,特别是一个知识板块中的几何内容,注意从前后一致、逻辑连贯的角度预设开课情境.像本课余角、补角的教学,很多教材上都是从一幅三角尺中两个锐角互余出发,引入新课,这种引入方式固然有一定的合理性,学生也能接触互余、互补的概念.然而从几何知识的逻辑严密性来看,前面刚学习线段、角的初步知识,并没有学习三角形内角和定理,而使用三角尺来引入余角的定义显得有些逻辑性上的缺陷.基于上述认识,我们选择了在图1中先画平角、再画直角、再画30°角这样渐进式画图的方式,呈现出一些角度之间的关系,既是对前面所学几何内容(特别是角的表示法及度量角度等)的复习,又为定义余角提供了有效的数学情境.从这个意义上看,我们所谓的“贴近学生最近发展区”就不仅是学生已有的经验,还需要从所教学内容的逻辑性、前后一致的高观点来审查、取舍教学情境的预设.
2.预设画图活动,发展学生几何文字语言与图形的对应能力
本课中,我们预设了多处画图活动,不仅开课时由教师示范作图,并成为开课阶段的一个有效的数学现实情境;在教学环节3中,又安排学生画一个直角的“双角平分线”图形,并经历度量、验证等环节,应该说前面的画图是发展学生几何文字语言与图形的对应能力,后面的验证则是初步训练学生的推理能力.根据教学经验,一些几何适应性偏弱的学生,常常是几何文字语言与图形之间的对应、转译能力存在障碍.一个教学现实是:不少学生面对文字命题常常表现出较低的适应性,而很多文字命题往往又会出现图形位置的不确定性,需要分类讨论.可见,几何起始阶段教学,重视文字语言与图形语言、符号语言之间的对应或转译是十分重要的.
3.辨别学段特征,几何起始教学时做好推理语句的示范与引领
初中几何学习不同于小学图形的学习,初中几何主要是欧氏几何系统,以训练学生的逻辑思维、理性精神为主.上述学段特征明确之后,就需要排除大量现实情境的干扰,引导学生善于抽象分离出几何图形并初步使用推理语言进行表达、推理或说明.在上面课例中,我们在环节2中,结合三角尺摆放后出现的α、β相等的情况,引导学生从推理的角度说明,借助学生在方程学习中已有的等式性质推理说明.事实上,就后续几何证题所需要的解题能力来看,等式性质参与下的几何解题技能是普遍使用的,特别是在全等三角形证明过程中对于间接条件的处理.
4.注重变式设问,培养学生洞察问题深层结构的能力
在教学环节3中,通过“双角平分线”基本图形的研究,引导学生感受这个问题结构与之前线段学习时积累到的“双中点”基本图形的经验,能培养学生洞察问题深层结构的能力.而这种深刻的洞察力、敏锐的捕捉力恰恰是后续繁杂图形问题能否快速贯通思路的关键.
三、结束语
有人说,越简单的教学内容往往越难教学.多轮循环教学之后,笔者教过“余角和补角”不下十余次,此前多是简单照搬教材内容,照本宣科,没有能从“教教材”走向“用教材教”.这次算是一次初步尝试,虽然获得听课同行的好评,也引发一些人的议论,期待听到更多的批判与建议,更欢迎类似案例跟进,让“用教材教”这种教学“风气”得到进一步传播.
参考文献:
1.严冬梅.辨识学段特征,重视推理训练——李庾南老师“余角与补角”课例赏析[J].中学数学(下),2015 (9).
2.中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
3.李庾南.自学·议论·引导教学论[M].北京:人民教育出版社,2013.
4.刘东升.辨别学段特征:初中几何教学的用力点——以“圆(第1课时)”教学为例[J].中学数学教学参考(中),2015(3).

