陈题改编:老歌如何新唱——以2015年上海市中考卷第25题的改编为例
☉江苏省如皋市九华镇九华初级中学 石高丽
陈题改编:老歌如何新唱——以2015年上海市中考卷第25题的改编为例
☉江苏省如皋市九华镇九华初级中学石高丽
中考复习备考期间,会有多轮的复习测试(或模考),试题的编拟虽然不能像期末卷、中考卷那样追求原创或深度改编,但尽量少用原题,减少直接“拿来主义”应该成为模考命题时的一种追求,将教材上的经典考题、本地区历年来的高频考题进行必要的变式改编,再用到模考卷中,即使有学生练习过原题,也能起到较好的检测反馈作用.本文讲述最近一次模考命题时笔者改编2015年上海市中考卷第25题的亲身经历,最后围绕陈题改编这个话题阐释几点思考,提供研讨.
一、2015年上海市中考卷第25题的变式与改编


图1
(1)求证:AP=OQ;
(2)求y关于x的函数关系式,并写出它的定义域;
(3)当△OPE是直角三角形时,求线段OP的长.
思路简述:(1)连接OD,证△AOP≌△ODQ,可得AP=OQ.(过程略)
(2)作PH⊥OA于点H.解Rt△OPH可用含x的代数式表示PH的长,则△AOP的面积可用含x的代数式表示.易证△PFC∽△PAO,根据相似三角形的面积比与对应边的比之间的关系可确定y关于x的函数关系式.
(3)当△OPE是直角三角形时,由于没有确定哪个角为直角,则需分∠POE=90°或∠OPE=90°或∠OEP= 90°三种情况进行分类讨论并取舍.


图2
(1)用含m的代数式表示DE的长;
(2)记△DEM的面积为S,求S关于m的函数关系式,并写出自变量m的取值范围;
(3)若动点N在弦CD上,且CN=OM,射线BM与射线OQ相交于点F,当△OMF是直角三角形时,求DE的长.

模考题:已知:如图2,半圆O的直径AB的长是20,弦CD∥AB,动点M在半径OD上,射线BM与弦CD相交于点E(点E与点C、D不重合).设OM=m.
(1)用含m的代数式表示DE的长;
①记△DEM的面积为S,求S关于m的函数关系式,并写出自变量m的取值范围;
②若动点N在弦CD上,且CN=OM,射线BM与射线ON相交于点F,当△OMF是直角三角形时,求DE的长.



图3
如图4,连接BC交OD于点M,作OG⊥CD于点G,所以CD=2CG.

图4
②分三种情况讨论:
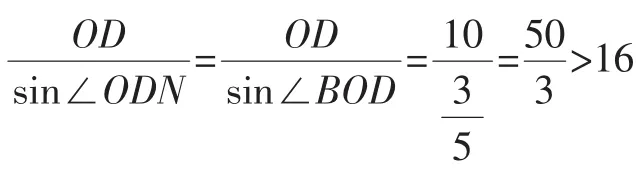

图5

图6


图7
(iii)∠OFM不可能为90°.理由如下,如图7,连接CO,因为OC=OD,所以∠C=∠D.因为CD//AB,所以∠D=∠BOD.所以∠C=∠BOD.
所以△OBM≌△CON(SAS),所以∠CNO=∠OMB.
又CD//AB,所以∠CNO=∠BON,所以∠BON= ∠OMB.在△BOF与△BOM中,∠BOF=∠OMB,∠B= ∠B,所以∠OFB=∠BOD.
因为∠BOD是锐角,所以∠OFB(即∠OFM)是90°这种情况不存在.
评分说明:第(2)问的第②小问主要考查学生对分类讨论思想掌握的熟练程度,需要分三种情况讨论,缺少一种扣1分.其中“∠OFM不可能为90°”说明方法不唯一,评卷时注意辨别学生不同的说理方式,不必拘泥于上述说理方式.
二、关于陈题改编的两点思考
1.精选陈题,明确训练方向
我们知道,教学中的三个经典问题(即教什么,教给谁,怎么教),作为陈题改编首先需要思考的仍然是“选什么”的问题,题海茫茫,陈题众多,复习阶段选择哪些陈题是每个编题者首先要思考的.笔者基于多年教学实践,提出一些个人的经验:第一,认真研究教材例习题,对那些揭示问题深层结构的优秀教材例习题要多选,功利一点说,各地中考命题也是以课本为本,绝大多数中考题多源自教材;第二,认真研究本地区近五年中考试题,挑出一些有关联的、富于变式的经典考题进行变式考查,这样复习下来就能让学生熟悉本地区考查的风格、难度、题型等,做到有备而无患,也所谓知己知彼;第三,关注北京、上海或较大的省会城市的中考数学卷,客观地说,这些地区的命题组实力相对较强,对数学的理解、对学生的理解、对教学的理解都显示出深厚的功夫.
2.陈题改编,老歌唱出新意

三、结束语
本文以一道考题的变式改编为例,兼说了陈题改编的两点思考,辞不达意,主体还是呈现了一道考题的改编,特别是参考答案与评分标准的制定,这也是想着重表达一种认识:行胜于言.因为与更多的立意阐释相比,能否精选陈题、恰当变式,提供给学生高质量的复习资料,做到精准备考,特别是,在顾及学生眼前利益的同时也能通过这些变式问题的训练促进学生变得更聪明、更智慧.
参考文献:
1.章建跃.发挥数学的内在力量,为学生谋取长期利益[J].数学通报,2013(2).
2.贺信淳.从多角度审视一道中考试题说开去——谈对初中数学教育现状之惑[J].数学通报,2013(12).
3.何明.由博返约,追求简约——一道“双曲线”综合题的命题过程[J].中学数学(下),2015(11).

