一道新定义考题的思路突破与教学思考

☉江苏省如皋初级中学　季　群



一道新定义考题的思路突破与教学思考

☉江苏省如皋初级中学季群

关注北京市近年来中考数学试题的同行应该知道，“新定义”把关题成为地方命题特色，作为一种风向标考题，北京市各区、各校各自的期中、期末试卷的把关题也都把“新定义”考题作为一道必考题.本文选取最近北京海淀区九年级第一学期期末卷上的把关题，首先展开思路贯通，并围绕该题给出教学设计，供研讨.

一、考题与思路突破

考题：（2015-2016学年北京海淀区九年级第一学期期末数学试卷，第29题）在平面直角坐标系xOy中，定义直线y=ax+b为抛物线y=ax2+bx的特征直线，C（a，b）为其特征点.设抛物线y=ax2+bx与其特征直线交于A、B两点（点A在点B的左侧）.

（1）当点A的坐标为（0，0），点B的坐标为（1，3）时，特征点C的坐标为_______.

（2）若抛物线y=ax2+bx如图1所示，请在所给图中标出点A、点B的位置.

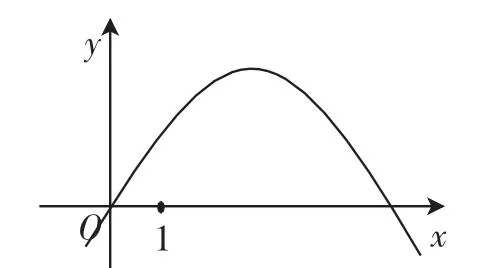
图1

（3）设抛物线y=ax2+bx的对称轴与x轴交于点D，其特征直线交y轴于点E，点F的坐标为（1，0），DE∥CF.

①若特征点C为直线y=-4x上一点，求点D及点C的坐标；

思路突破：对于（1），关键是确定a、b的值，只要把点A的坐标（0，0）、点B的坐标（1，3）代入直线y=ax+b的解析式即可求出a、b的值，从而明确特征点C的坐标为（3，0）.

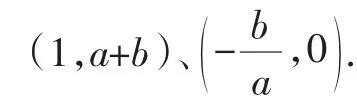
图2

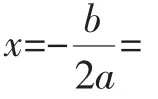
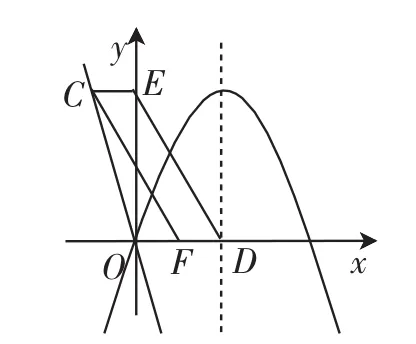
图3

图4

②这是一个填空题，然而情况较复杂，要想获得解答，需要深入思考，主要是a、b的取值范围不同，有不同的构图需要考虑.

（i）当a＜0、b＞0时，构图（如图4，注意：点D应该在点F的右边，否则不能符合DE∥CF）.

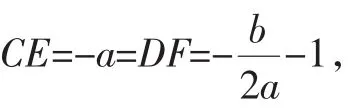
图5

（ii）当a＞0、b＜0时，构图（如图6、图7）.

图6

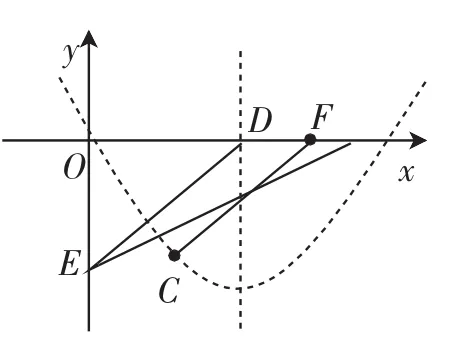
图7

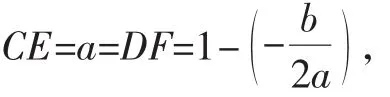
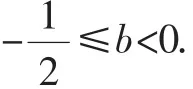
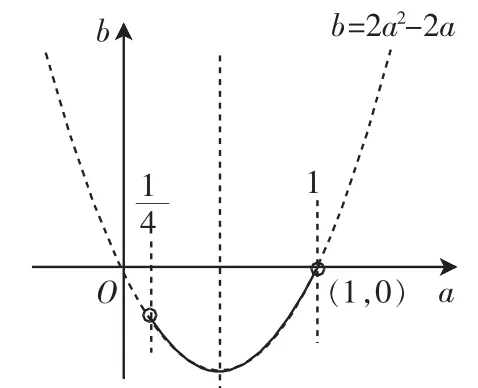
图8

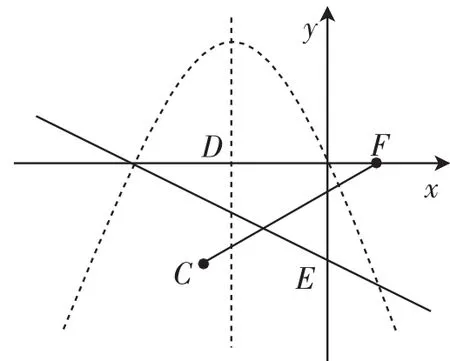
图9

（iii）当a＜0、b＜0时，构图（如图9），容易发现，此时特征点C在第三象限，不符合DE∥CF，故此种情况舍去.

（iv）当a＞0、b＞0时，构图（如图10）.

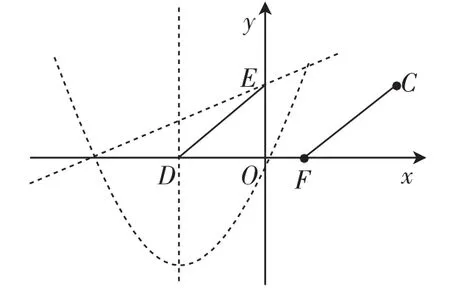
图10

二、解后回顾与赏析

这道新定义考题经过以上思路突破获得了解答，为了避免“入宝山而空返”，下面再给出必要的回顾与赏析.

1.思路贯通的关键

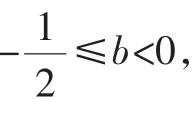
2.数形结合的思想

除初始问题并不一定要构造出图形辅助思考，后续问题都需要构造出恰当的图形辅助思路，在最后一问的四种情况讨论时，更是需要画出可能的图形，求解过程中以形助数、数形互助的求解策略体现得十分充分，值得认真体会.

3.前后呼应的设计

红楼梦的艺术特色是“草蛇灰线，伏脉千里”，本题的几个设问充分体现了这一艺术特色.具体来说，初始问题帮助理解新定义，接下来画出两个交点为后续第三问研究提供了必要的基础，防止部分学生还不能明确两个交点的特点；在（3）①中，先给出一个特例引路，让点C在直线y=-4x上，帮助学生确认可能的图像位置，与（2）中的图像做到一次呼应；又启发和引导着（3）②研究的路径与方法，环环相扣，渐入佳境，易进难出，是一道不可多得的把关试题.

三、考题的解题教学设计

设想针对本题开展试题讲评或以该题为例开展解题教学，以下给出围绕该考题的解题教学的简要教学设计.

环节（一）开课阶段，熟悉“定义”

给出定义：在平面直角坐标系xOy中，定义直线y= ax+b为抛物线y=ax2+bx的特征直线，C（a，b）为其特征点.

问题1：当点A的坐标为（0，0）、点B的坐标为（1，3）时，求特征点C的坐标.

追问1：在“问题1”条件下，此时抛物线y=ax2+bx与其特征直线是否有交点？如果有，写出两点的坐标；如果没有，说明理由.

追问2：设抛物线y=ax2+bx与其特征直线交于A、B两点（点A在点B的左侧）.若抛物线y=ax2+bx如图1所示，请在图中标出点A、点B的位置.

环节（二）运用“定义”，展开研究

问题2：设抛物线y=ax2+bx的对称轴与x轴交于点D，其特征直线交y轴于点E，点F的坐标为（1，0），DE∥CF.

追问1：当a<0、b>0时，试写出b关于a的函数关系式.

追问2：若特征点C为直线y=-4x上一点，求点D及点C的坐标.

环节（三）变式再练，检测反馈

根据多年来解题教学的经验，如果教师只是满足于课堂上讲解、启发或部分追问一些学生的理解，则很多学生即使听懂了，依然不会做，更不能深刻理解类似的较难试题，这里一个可行的办法就是在讲解之后，将问题做简单的变式改编后安排学生限时再练，检测反馈，这样往往能取得较好的教学效果.限于篇幅，我们不给出变式题，比如将问题中的系数a、b改成“直线y=mx+n为抛物线y=mx2+nx的特征直线”就是一种可行的简单改编，或者把后续问题的呈现台阶再次增加，比如在第三问增加“当m>0、n>0时，试写出n关于m的函数关系式”等.

四、继续思考

参考文献：

1.肖维松.回到概念：解题教学的一种取向——以2014年江苏泰州卷第25题教学为例［J］.中学数学教学参考（中），2014（7）.

2.罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，2008.

3.【美】波利亚，著.怎样解题［M］.阎育苏，译.北京：科学出版社，1982.

4.邓东皋，孙小礼，张祖贵.编.数学与文化［M］.北京：北京大学出版社，1999.