分层导学：在层和导上“做文章”——以“直线、射线、线段”复习为例

☉江苏省如皋市石庄镇初级中学　张　霞



分层导学：在层和导上“做文章”——以“直线、射线、线段”复习为例

☉江苏省如皋市石庄镇初级中学张霞

合作学习是目前较为流行的一种学习方式，在很多地方的数学课堂中得到了广泛的应用.作为合作学习的重要补充，分层导学对每一名学生的发展都有着巨大的推动作用，所以，分层导学被很多老师应用到初中数学课堂中.为了将“分层导学”的教学应用进一步推进，我市近期举行了“分层导学”专题研讨活动，笔者有幸开设了一节公开课.现结合这节公开课上的一则教学片断谈谈笔者的感悟，不足之处敬请指正.

一、例题设置及分析

1.例题

A级：如图1，点M为线段AB的中点，点C将线段MB分成MC∶CB=1∶3，若AB=16cm，求线段AC的长.

图1

B级：如图1，点M为线段AB的中点，点C将线段MB分成MC∶CB=1∶3，若AC=10cm，求线段AB的长.

C级：已知点M为线段AB的中点，点C在线段AB上且满足MC∶CB=1∶3，若AC=10cm，求线段AB的长.

教学要求：请同学们阅读上面三级例题，并从中选择一道你能够解答的最高级例题进行求解.完成解答后，到对应的交流区交流以下内容：（1）解题结果；（2）解题思路；（3）解题注意点.

2.简析

三级例题梯度明显：A级题，线段计算中的基础题，难度很小；B级题，三个条件关联不大，直接推理得出结果较难，如果能设未知数建立方程的模型来化解问题应该不是难事，所以将此题编排给班级中等学生解答；C级题，本题直接以文字语言形式出现，学生需要认真阅读，并根据点C的位置分类讨论，用图形直观呈现出问题情境，再去利用化解B级题的方法求解，很明显，C级题为学生留出了探索的空间，适宜于班级中学有余力的学生解答.

张奠宙教授说“变式练习是中国教育的一个创造”.这里，教者以B级题为原型，通过难度的增减实现了例题的梯度设计.与例题配套的教学要求将学生的解题目标和交流内容进行了明确，为学生进行自主探索交流指明了方向.

二、教学片断

根据“教学要求”，学生阅读三级例题，并选择自己能够解答的最高级别例题自主解答.8分钟后，学生进入对应交流区展开小组交流，教师巡视指导，并参与部分小组的交流.5分钟后，教师让学生再度熟悉了一下这里的三级例题，接下来对这三道例题进行了全班交流.

教师：我们先请解答A级例题的同学来交流一下你们的解题过程.

学生1：根据条件“MC∶CB=1∶3”，我设MC=xcm，则CB=3xcm.所以，MB=4xcm.根据“点M为线段AB的中点”可得AB=2MB=8xcm，AM=BM=4xcm，这样一来，我们就可以得到方程8x=16，所以x=2.易得AC=AM+MC=5xcm= 10cm.

学生2：我是用比例来做的.

教师：说说你的过程.

学生2：根据“MC∶CB=1∶3”，可得MC∶MB=1∶4.由“M为线段AB的中点”，得AM=BM=AB=8cm，MC∶AB=1∶8.所以MC=AB=2cm.易得AC=AM+MC=10cm.

教师：看来，无论是列方程还是用比例，都能得出最终的答案.那么，细细分析这两种解法，哪一种更简单些呢？

学生3：列方程简单些，而且解题过程容易说清楚.

教师：好的！学习了一元一次方程后，在解决问题时，我们要努力用好这一数学模型.接下来的B级题目也用到方程了吗？

学生（齐）：用到了！

教师：具体说说！

学生4：还是设MC=xcm，则CB=3xcm.易得AB=2MB= 8xcm，AM=BM=4xcm.所以AC=AM+MC=5xcm.得方程5x= 10.所以x=2.所以AB=16cm.

教师：用比例的方法也可以解吗？

学生5：可以，和问题1中用比例求解过程基本差不多，比方程求解要烦一点点.

教师：嗯！看来方程真是解决问题的好工具.来看C级问题.

学生6：C级例题比B级例题难了不少.首先，题目中没有图形，要作图.“点C在线段AB上”，C点的位置没有确定是在M点的哪一侧，所以，这里要结合“MC∶CB=1∶3”分类作图.图1是其中的一种情形，图2中点C在点M的左侧，这是另一种情形.

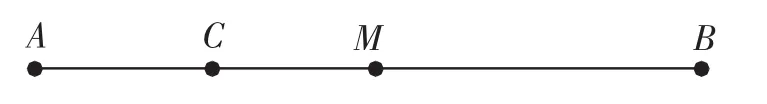
图2

教师：根据这两幅图，你能分别求出AC的长吗？

学生6陈述求AC长的过程，教师将其解题过程同步投影并进行了点评.

教师：通过这三道例题的解答与交流，你有哪些收获？

学生7：我知道了线段的计算也可以用一元一次方程求解.

学生8：这里的C级题目没有图形，遇到此类题目时，我们要根据题意作出图形，再去求解.

学生9：就是要数形结合呗！

学生10：我觉得作图的时候，还要考虑点的不同位置，必要时，应分类讨论.

教师：是的！随着学习的深入，不光要关注点的位置，有时还要从线或组合图形的位置的角度进行分类.今天的这些收获，对我们今后学习数学是很有帮助的.

三、片断分析

为了突出“分层导学”的研讨专题，教者从多个角度进行了精心设计.无论是教师的教学预设，还是学生的丰富生成，都很好地诠释了分层导学的内涵.学生的选择解答将分层的主动权交给了学生，他们在对三级例题详细阅读后，作出了符合自己探索需求的解答选择，这样的过程经历，给下面的小组与全班交流积累下很多可用的素材.于是交流时，每一个个体都有发出自己的声音的机会与权力，他们在组内和班上对不同级别的例题给出了两种不同角度的解法.一种来自于小学中“比例”认知的自然延续，另一种则来自于上一单元“一元一次方程”的适度延伸，一切都十分自然.全班交流，教师引导学生从A级例题开始，将数学认知水平较低的同学推上了前台，步步追问，让例题的交流从低级逐步走向高级，学生的数学思维不断深入，每一名学生的“学有所获”成为了现实.

四、两点感悟

1.分层导学应给予学生选择的机会

正如片断分析中所说，教学不仅要强化学生学习的内在驱动，还要彰显教师的人文情怀.给学生自主选择的机会，这不仅体现对学生的尊重，还让学生在有限的时空中最大可能地发挥出自己的潜能，使得其在数学上得到最大幅度的发展.因此，我们应给予学生自主选择解答例题的机会，让他们在读题后很好地认识自己的现状，知晓自己的知识与能力，并作出符合自己知识与能力现状的选择，从而推动每一名学生在自己所能达到的最大高度上尽快地成长.

2.解题要求及交流提示要清晰明了

基于“分层导学”的教学，教师是课堂的组织者、引导者，在教学中最大的作用就是“穿针引线”.所以，发给学生的导学案（或学习单、导学单、活动单等）应对学生的活动提出明确的要求，尤其是例题教学的要求应十分明确.教学设计时，不仅要有呈现明确的解题要求，还应给出具体的交流要求，要说清在什么时候交流什么内容，甚至连交流到何种程度都可以一并在给出的学习材料中加以展示.确保学生学习过程能按照既定的步骤稳步前进，不受太多的干扰.