纵横交叉算法在配电网故障定位中的应用

殷 豪，李德强，孟安波，魏明磊，洪俊杰

纵横交叉算法在配电网故障定位中的应用

殷 豪，李德强，孟安波，魏明磊，洪俊杰

(广东工业大学，广东 广州 510006)

基于人工智能算法具有较好的容错性，引入纵横交叉算法(CSO)应用在配电网故障定位过程中。CSO中的横向交叉机制和纵向交叉机制在与竞争算子的配合下提供了较强的搜索能力，能够快速解决多变量非线性优化问题，为准确解决故障定位提供了基础。在多电源分区故障定位中改进适应度函数，对不同区域适应度函数设置区域权值，区域权值由反馈故障电流决定。这种设置方式可以增强算法的容错性，使得输出结果不会因为故障信息在传送过程中发生畸变而误判或者漏判。仿真部分由双电源配电网系统和三电源配电网系统组成，并通过算法进行了验证，每次反馈信息都由一次正常信息和畸变信息组成。从仿真结果可以看出CSO拥有较强的稳定性。

纵横交叉算法(CSO)；故障定位；适应度函数；容错性；稳定性

0 引言

随着配电网智能运行水平提高，配电网自动化技术应用不断增加。故障定位是实现配电网自动化技术的一个重要分支[1-2]，其原理是通过馈线终端单元(Feeder terminal unit，FTU)和远程终端单元(Remote terminal unit)等自动化设备实现对网络信息的实时监测和通报，在由控制系统进行信息处理得出故障位置，精确的故障定位可以提高供电可靠性和系统稳定性。

目前，常用的故障定位方法有两类：一类是直接法，这种方法以矩阵算法[3-4]为代表，矩阵算法具有着实时定位故障位置的特点，是故障定位的常用方法。但是，因为终端设备通报的信息存在误报和漏报，使得数据处理出现差错，最终导致出现误判情况，这种因素使得矩阵算法受到了一定的限制。随着人工智能算法的不断发展，众多专家采用人工智能算法解决电力领域相关问题[5-7]，其中应用在故障定位中的有遗传算法[8-9]、蚁群算法[10-11]、粒子群算法[12]、蝙蝠算法[13]。这些算法具有容错性高和并行处理优化问题的能力。如文献[8]，充分利用遗传算法 0、1编码方式的优势来表示配电网的运行状态，在通过遗传、交叉和变异来对适应度函数寻优，其中适应度函数进行了改进，避免了故障定位中一值多解的问题。文献[10]是改进蚁群算法运用到配电网故障定位中，其中蚁群算法的正反馈能够提高运算速率、分布式计算能够跳出寻优过程中的早熟问题，这些优势都能够提升故障定位程序运行的效率。

本文在配电网故障定位的求解中应用CSO[14]，这种算法采用双搜索机制分别是横向交叉算子和纵向交叉算子，搜索过程是横向交叉算子和纵向交叉算子共同搜寻问题的最优解。在配电网故障定位中，横向交叉算子是两个不同的解之间的所有维进行的一种运算；纵向交叉算子是同一个解不同维度之间的运算，这种机制提升了故障定位容错性，充分利用故障信息的关联性。竞争算子是淘汰掉适应度差的解，使得算法收敛加快。目标函数结合文献中提出的方法并进一步改进，具体是通过故障电流回馈信息构造函数阀值。这种方法使得目标函数不会因为信息畸变而导致错误判断故障位置。仿真部分是由两个典型的配电系统组成，结果证明CSO具有较好的容错性和较强的稳定性。

1 CSO故障定位的基本原理

CSO由3部分组成，分别是横向交叉算子、纵向交叉算子和竞争算子。其搜索过程是粒子经过横向交叉运算后引入竞争算子，保留适应度更强的粒子参与纵向交叉运算过程，然后经过纵向交叉运算后引入竞争算子，接着将两代粒子中适应度更强的粒子保留到下一次迭代运算。

1.1 编码方式

编码方式是整体运算的前提，故障定位的编码通常采用0和1的编码方式，0表示网络设备正常状态，1表示设备故障状态。整体网络用0和1数字组成的字符串来表示其对应设备的状态。

1.2 横向交叉算子

横向交叉算子是两个不同解所有维交叉的一种算术交叉。假设交叉前的解为父代解，则交叉后的解为子代解，具体公式为

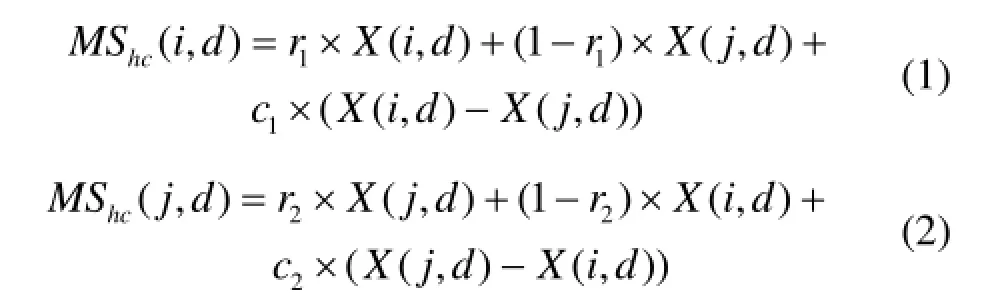
式中：r1和r2是0~1之间的随机数；c1和c2是-1~1之间的随机数。X(i, d)和X(j, d)是两个不同的父代解；MShc(i, d) 和MShc(j, d)是父代解经过运算后的子代解。解的构成是字符串所表示的网络设备状态。

1.3 纵向交叉算子

纵向交叉算子是把一个解的不同维度交叉的一种算术运算。交叉前的解为父代解，交叉后的解为子代解，具体公式为

式中：r是0~1之间的随机数；MSvc(i, d1) 是个体X(i)不同维度纵向交叉产生的后代。

1.4 竞争算子

竞争算子是父代与子代的一种淘汰机制，将父代解与子代解的适应度进行对比，保留适应度更强的解参与下一次迭代。流程图如图1。

图1 竞争算子的流程Fig. 1 Procedure of the competitive operator

竞争算子是解群进化的一个重要机制，通过设定一定的竞争率使得整体解群朝着最好的方向前进。

1.5 运算后的离散化

在经过横向交叉算子和纵向交叉算子后的解不能维持设备表示的状态(0和1)，这时引入阀值函数将运算后的解离散化。离散化约束条件为

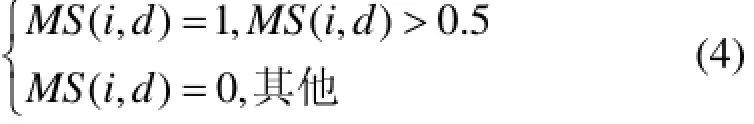
MS(i, d)是经过交叉运算后得出第i个解的第d维，经过离散化后的解就可以参与整体运算。

2 配电网故障定位的数学模型及原理

2.1 适应度函数

适应度函数是故障定位基础，在故障发生以后，测控点中FTU和RTU返回故障信息，将故障信息代入适应度函数中进行计算，接着用算法不断逼近故障信息即可得出故障位置。适应度函数为

式中：f(X)为目标函数的适应度；X为网络中设备状态；Ij为第j个测控点中FTU和RTU返回的实际状态，0表示测控点上没有流过过电流，1表示测控

一个简单配电网（图 2）为例对期望状态模型做如下解释。

图2 单电源辐射配电网Fig. 2 Radiate distribution network of single power source

图中的 CB1是进线断路器，S1~S3是均装有FTU的分段开关，Z1~Z4是4段馈线，期望状态模型为

式中：x(1)~x(4)是馈线区段(设备)的状态信息，0表示正常，1表示故障；Ú为逻辑或运算。

测控点中上传的实际数据与测控点期望状态相差最小时，得出计算出的故障位置。所以故障定位就是寻找式(5)中的最小解。

由式(6)—式(9)可知，当馈线Z4发生故障，测控点返回电流I1、I2、I3、I4全部为1，为了使适应度函数最小，应全部为1，但是此时中的x(1)~x(3)可以为1也可以为 0，两种取值不影响其最终结果，但是容易输出错误故障位置，造成误判。这是因为逻辑Ú的运算产生的影响。根据故障诊断理论中的 “最小集”概念，这时对适应度函数进行改进如式(10)。式中：x(j)是配电网中第j段馈线的状态信息，0表示处于正常状态，1表示故障状态；w是设备故障数和的系数，通常取0.5。

改进后的适应度函数可以减少误判的问题，能提高算法的正确率。当图2中的Z4段发生故障时，情况如下：

(1) 测控点返回电流1I,2I,3I,4I值均为1，此时为了使f(x) 最小，也应该为1，当w取值为0.5时，如果x(1)~x(3)取值为0，x(4)取值为 1，式(10)中的第一项为 0，第二项为0.5，f(x)为0.5。

(2) 测控点返回电流1I,2I,3I,4I值均为1，此时为了使f(x) 最小，也应该为 1，如果 x(1)和x(3)取值为0，x(2)、x(4)取值为1，式(10)中的第一项为0，第二项为1，f (x)为1。

根据适应度函数的目标函数取最小值，(1)中的结果比(2)中的小，所以采用(1)，输出结果如表1。

表1 优化结果Table 1 Results of optimization

可以看出状态信息与故障位置相同，得出最佳结果，说明改进后的适应度函数具有良好的容错性。

2.2 双电源分区故障

环网开环运行的配电网中，因为联络开关的作用使得不同的配电区域相互不受影响。文献[15-16]都提到了关于配电网分区故障定位问题。其中文献[15]中改进了期望函数模型，设定了每个区域故障个数，从而使得模型减少了误判的可能性。同时每个区域的适应度函数设定一个权重因子，当与权重因子相对应的区域发生故障时，赋值为1，否则为0。文献[16]中根据首段变电站变压器低压侧开关是否上报故障信息为依据，来判断故障发生区域。同时将上报信息的权重因子赋在不同区域的适应度函数上，当对应区域发生故障时赋值为 1，没有发生时赋值为 0。但是没有考虑到首段反馈信息在传输过程中发生畸变的情况，这样容易出现漏判情况，降低了算法的容错性。

本文改进权重因子，将权重因子设定与对应区域的所有回馈电流相关联，这样的设定方法增加了算法的容错性，使得算法不会因为某一个回馈信息发生畸变而出现漏判情况。

图3中的CB1和CB2为进线断路器，S1~S3、S5~S7是均装有FTU的分段开关，Z1~Z8是8段馈线，SL是联络开关，A和B是以联络开关为分界线的两个区域。对于分区的配电网络的适应度函数改进如下。

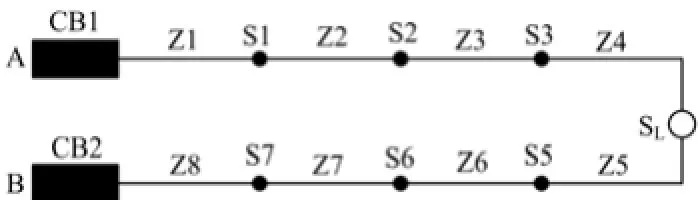
图3 双电源开环运行配电网Fig. 3 An open-loop operating distribution network with double power sources

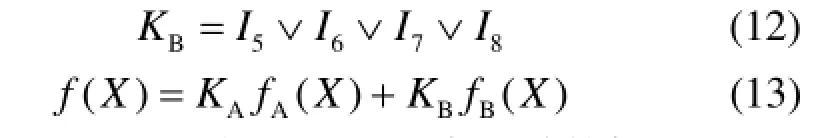
式中：KA和KB分别为A和B两个区域的权重因子；I1~I8是图2中FTU和RTU返回的实际状态，0表示测控点上没有流过过电流，1表示测控点流过过电流；fA(X)和fB(X)的公式如式(10)所示。可以看出这样构造权重因子的方法可以改变因为反馈电流信息发生突变而出现的误判。图3的期望状态模型为

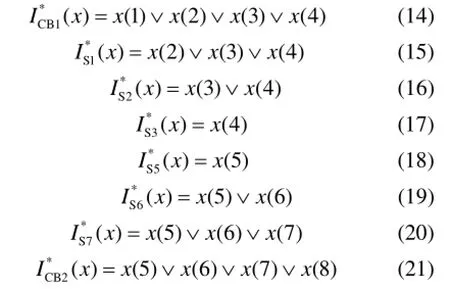
2.3 算法流程图(图4)

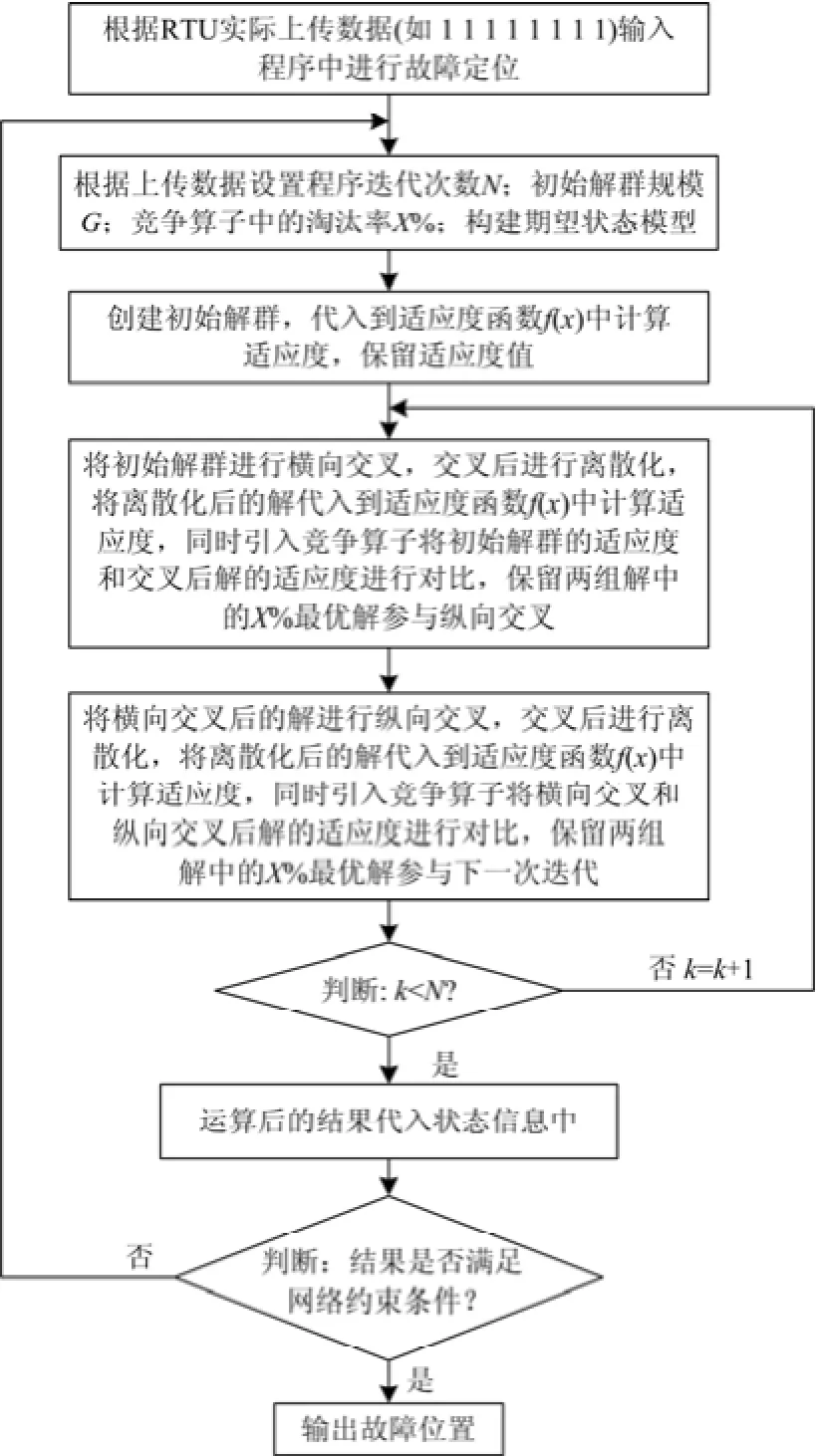
图4 CSO流程图Fig. 4 CSO algorithm flow chart

3 算例

3.1 算例1

如图3中的简单配电网所示，FTU上传三组信息分别是A区单一故障、B区单一故障和A和B区同时单一故障，每组包括一个正常故障信息和一个畸变信息, 故障发生位置分别在 Z4、Z5、Z4和Z5。同时设置算法的迭代次数为30，及初始解群规模为10，竞争算子的淘汰率为50%。将以上信息输入到故障定位的程序中，得出结果如表2所示。

信息状态 上传信息 测试结果第一组 畸变 00001101 00001000正常 11110000 00010000正常 00001111 00001000第二组 畸变 10110000 00010000第三组 畸变 10111101 00011000正常 11111111 00011000

由表2可以看出在得到三组反馈信息后，输入到CSO中进行故障定位都能得到正确的故障位置，同时算法能包容上述的畸变信息，说明CSO在双电源开环运行的配电网中具有良好的容错性。

3.2 算例2

图5是一个典型配电网，CB1~CB3为进线断路器，S1~S8为均装有FTU的分段开关，Z1~Z12为馈线， SL1~ SL3是联络开关，A、B、C是以联络开关为分界线的三个区域。同时设置算法的迭代次数为 30，初始解群规模为 10，竞争算子的淘汰率为50%。其中带箭头的是发生故障的区域，可以看出每个区域均发生单一故障。

图5 三电源开环运行配电网Fig. 5 An open-loop operating distribution network with three power sources

将3种故障情况输入到程序中运算，得出以下结果。

1) 当图5中发生单一故障时，故障点发生在Z4馈线段上，信息在没有发生畸变的情况下，上传信息是[11110 00000 00]，输入到程序中得出测试结果是[00010 00000 00]。当输入信息发生畸变时上传信息是[11110 00100 00]，得出测试结果是[00010 00000 00]。

2) 当图5中发生复故障时，故障点发生在Z4、Z7馈线段上，信息在没有发生畸变的情况下，上传信息是[11111 11000 00]，输入到程序中得出测试结果是[00010 01000 00]。当输入信息发生畸变时上传信息是[11011 11000 00]，得出测试结果是[00010 01000 00]。

3) 当图5中发生复故障时，故障点发生在Z4、Z7、Z12馈线段上，信息在没有发生畸变的情况下，上传信息是[11111 11011 01]，输入到程序中得出测试结果是[00010 01000 01]。当输入信息发生畸变时上传信息是[11110 11011 01]，得出测试结果是[00010 01000 01]。

为了验证算法的容错性和稳定性，将以上 6种情况输入到程序当中，每种进行20次运算，结果如表3。

表3 三电源分区故障测试结果Table 3 Results of failure which happens in three source

从表3中可以看出，仅在Z4、Z7、Z12点发生故障及没有畸变信息时发生了一次误判，其余均没有误判发生，说明本文提出的CSO具有较强的稳定性。

4 结论

本文提出将 CSO应用于配电网故障定位过程中，同时用双电源配电系统和三电源配电系统作为仿真系统得出以下结论：

1) CSO在配电网故障定位中拥有较强的搜索能力和较好的鲁棒性，为快速解决故障定位提供了基础。

2) 通过改进适应度函数使得算法的容错性增强，从算例1和算例2的测试结果中可以看出，在解决多电源分区故障定位的问题上大大减少了因为信息畸变而发生的误判或漏判。

3) 同时从算例中可以看出 CSO不会因为系统规模的改变而变化，所以此算法可以应用在大规模的配电网系统中进行故障定位。

[1] 孙刚, 时伯年, 赵宇明, 等. 基于MMC的柔性直流配电网故障定位及保护配置研究[J]. 电力系统保护与控制, 2015, 43(22): 127-133.

SUN Gang, SHI Bonian, ZHAO Yuming, et al. Research on the fault location method and protection configuration strategy of MMC based DC distribution grid[J]. Power System Protection and Control, 2015, 43(22): 127-133.

[2] 范国琛, 朱永利, 史金茂, 等. 基于Kaiser自卷积窗的相位比较式输电线路故障定位方法[J]. 电力系统保护与控制, 2015, 43(7): 143-148.

FAN Guochen, ZHU Yongli, SHI Jinmao, et al. Fault location scheme for transmission lines using Kaiser selfconvolution windowed FFT phase comparison[J]. Power System Protection and Control, 2015, 43(7): 143-148.

[3] 夏雨, 姚月娥, 刘全志, 等. 配电网故障定位和隔离的新统一矩阵算法[J]. 高电压技术, 2002, 28(3): 4-5, 8.

XIA Yu, YAO Yuee, LIU Quanzhi, et al. A new general matrix arithmetic on the location and isolation of the fault section in power distribution networks[J]. High Voltage Engineering, 2002, 28(3): 4-5, 8.

[4] 王飞, 孙莹. 配电网故障定位的改进矩阵算法[J]. 电力系统自动化, 2003, 27(24): 45-46, 49.

WANG Fei, SUN Ying. An improved matrix algorithm for fault location in distribution network of power system[J]. Automation Electric Power Systems, 2003, 27(24): 45-46, 49.

[5] 赵阳, 夏欢, 邱晓晖, 等. 基于独立分量分析算法的医疗电子设备辐射电磁干扰EMI噪声分析方法[J]. 电工技术学报, 2015, 30(17): 180-190.

ZHAO Yang, XIA Huan, QIU Xiaohui, et al. The radiated EMI analysis method for electromedical equipments based on ICA[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 180-190.

[6] 龙虹毓, 张晓勇, 胡晓锐, 等. 蚁群优化小波阈值算法用于变电设备状态信号提取[J]. 电工技术学报, 2015, 30(12): 422-428.

LONG Hongyu, ZHANG Xiaoyong, HU Xiaorui, et al. Extraction of condition signals of electrical plants by ACO wavelet threshold estimation[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 422-428.

[7] 叶满园, 周琪琦, 蔡鸿, 等. 基于多种群遗传算法的多电平逆变器多波段SHEPWM技术[J]. 电工技术学报, 2015, 30(16): 111-119.

YE Manyuan, ZHOU Qiqi, CAI Hong, et al. Multiplepopulation genetic algorithm based on multi-band SHEPWM control technology for multi-level inverter[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 111-119.

[8] 郭壮志, 陈波, 刘灿萍, 等. 基于遗传算法的配电网故障定位[J]. 电网技术, 2007, 31(11): 88-92.

GUO Zhuangzhi, CHEN Bo, LIU Canping, et al. Fault location of distribution network based on genetic algorithm[J]. Power System Technology, 2007, 31(11): 88-92.

[9] 杜红卫, 孙雅明, 刘弘靖, 等. 基于遗传算法的配电网故障定位和隔离[J]. 电网技术, 2000, 24(5): 52-55.

DU Hongwei, SUN Yaming, LIU Hongjing, et al. Fault section diagnosis and isolation of distribution network based on genetic algorithm[J]. Power System Technology, 2000, 24(5): 52-55.

[10] 王林川, 李庆鑫, 刘新全, 等. 基于改进蚁群算法的配电网故障定位[J]. 电力系统保护与控制, 2008, 36(22): 29-33, 53.

WANG Linchuan, LI Qingxin, LIU Xinquan, et al. Distribution network fault location based on the improved ant colony algorithm[J]. Power System Protection and Control, 2008, 36(22): 29-33, 53.

[11] 陈歆技, 丁同奎, 张钊. 蚁群算法在配电网故障定位中的应用[J]. 电力系统自动化, 2006, 30(5): 74-77.

CHEN Xinji, DING Tongkui, ZHANG Zhao. Ant colony algorithm for solving fault location in distribution networks[J]. Automation of Electric Power Systems, 2006, 30(5): 74-77.

[12] 李超文, 何正友, 张海平, 等. 基于二进制粒子群算法的辐射状配电网故障定位[J]. 电力系统保护与控制, 2009, 37(7): 35-39.

LI Chaowen, HE Zhengyou, ZHANG Haiping, et al. Fault location for radialized distribution networks based on BPSO algorithm[J]. Power System Protection and Control, 2009, 37(7): 35-39.

[13] 付家才, 陆青松. 基于蝙蝠算法的配电网故障区间定位[J]. 电力系统保护与控制, 2015, 43(16): 100-105.

FU Jiacai, LU Qingsong. Fault sections location of distribution network based on bat algorithm[J]. Power System Protection and Control, 2015, 43(16): 100-105.

[14] MENG A, CHEN Y, YIN H, et al. Crisscross optimization algorithm and its application[J]. Knowledge-Based Systems, 2014, 67(3): 218-229.

[15] 卫志农, 何桦, 郑玉平. 配电网故障区间定位的高级遗传算法[J]. 中国电机工程学报, 2002, 22(4): 127-130.

WEI Zhinong, HE Ye, ZHENG Yuping. A refined genetic algorithm for the fault sections location[J]. Proceedings of the CSEE, 2002, 22(4): 127-130.

[16] 郑涛, 潘玉美, 郭昆亚, 等. 基于免疫算法的配电网故障定位方法研究[J]. 电力系统保护与控制, 2014, 42(1): 77-83.

ZHENG Tao, PAN Yumei, GUO Kunya, et al. Fault location of distribution network based on immune algorithm[J]. Power System Protection and Control, 2014, 42(1): 77-83.

(编辑 周金梅)

Fault location for distribution network based on crisscross optimization algorithm

YIN Hao, LI Deqiang, MENG Anbo, WEI Minglei, HONG Junjie
(Guangdong University of Technology, Guangzhou 510006, China)

Based on good fault tolerance performance of artificial intelligence algorithm, crisscross optimization algorithm (CSO) is applied in the process of fault location for distribution network. In the CSO algorithm, the horizontal crossover mechanism and the vertical crossover mechanism in cooperation with competitive operator provide strong search ability, which could quickly solve multi variable and nonlinear optimization problems and supply the basis foundation to solve fault location problems. Improving fitness function in the multi-source sections fault location problem and setting section weight values for different section fitness functions, this setting mode can enhance fault tolerance of algorithm, then the output results won’t erroneous judgment or missing judgment when the fault message distorted during the transformation. The simulation part is composed of the distribution networks system of double and third power sources, which is verified by the algorithm. The regular message and distortion message make up the each time feedback message. The results prove that CSO algorithm has strong stability. This work is supported by National Natural Science Foundation of China (No. 51407035).

crisscross optimization algorithm (CSO); fault location; fitness function; fault-tolerance; stability

2015-10-31；

2016-03-01

殷 豪(1972-)，女，硕士，副教授，研究方向为电力系统稳定与控制；E-mail: 523539650@qq.com

李德强(1991-)，男，通信作者，硕士研究生，主要研究方向为智能算法在电力系统中的应用；E-mail: 928752686@qq.com

孟安波(1971-)，男，博士，副教授，研究方向为人工智能算法在电力系统中的应用。E-mail: menganbo@vip. sina.com

10.7667/PSPC151919

国家自然科学基金资助项目(51407035)