一种基于拉格朗日插值的微网虚拟功率下垂控制方法

颜湘武，王星海，王月茹

一种基于拉格朗日插值的微网虚拟功率下垂控制方法

颜湘武，王星海，王月茹

(华北电力大学电气与电子工程学院，河北 保定 071003)

低压微电网线路阻性成分大，下垂控制的直接应用会导致功率的耦合问题，而经过坐标变换后的虚拟功率下垂控制方法可以实现功率的解耦控制。针对采用固定的虚拟功率下垂系数无法保证微网孤岛运行时的频率与电压质量的问题，提出了一种基于拉格朗日插值方法的虚拟功率下垂控制策略，可以保证当微源的输出功率不超过允许范围时，其频率与电压符合电能质量要求。为了实现并联微源输出功率的合理分配，加入了功率分配鲁棒控制方法，使得虚拟无功功率的分配不受线路阻抗影响。利用该方案对通过不同线路并联的两台同容量逆变器并联进行了仿真，并与固定下垂系数方法进行了对比分析。结果表明，新型下垂控制方法可以保证优质的电能质量与并联微源间功率的合理分配。

微电网；功率耦合；虚拟功率；拉格朗日插值；电能质量；功率分配

0 引言

伴随着全球能源的日益枯竭，新能源发电技术在世界范围内得到了大力推广与发展，大规模的分布式电源(Distributed Resources，DR)通过微网接入常规电网，微网存在联网与孤岛两种运行模式[1-2]。相对于单台大功率的逆变器而言，采用多台逆变器并联可以扩大供电系统的容量，其最突出的优点是可以实现稳定可靠的冗余供电[3]。下垂控制模拟了传统电网中同步发电机的调压调频特性，目前已被广泛应用于孤岛模式下多逆变器的并联控制中[4-5]，但由于低压微网线路的阻性成分大，各微源地理位置上具有分散性，线路阻抗大小存在差异，并联逆变器孤岛运行模式下的下垂控制需要解决功率耦合、电能质量及功率分配等问题。

针对低压微网的功率耦合问题，文献[6]提出了引入虚拟电抗以消除功率耦合的方法，文献[7]从理论上对虚拟电抗的解耦作用进行了论证，但引入较大的虚拟阻抗会影响电压质量[8]。文献[9]通过设计控制器参数，使逆变器的输出阻抗呈感性，但该方法受制于控制器参数。文献[10]提出了有功-电压、无功-频率反下垂控制方法，但该方法只适用于线路电阻远大于感抗的情况，不具有普遍适用性。文献[11]提出了虚拟电压-频率控制方法以实现功率解耦，但该方法不符合频率与电压的电能质量评价体系，难以在实际工程中应用[12]。

虚拟功率下垂控制方法[12-13]根据线路阻抗大小对功率进行线性组合，以得到虚拟有功与频率、虚拟无功与电压之间近似的对应关系，进而实现功率的解耦控制，具有普遍适用性。本文采用了该方法以实现低压微网的解耦控制，并提出了一种基于拉格朗日插值的虚拟功率下垂控制方法，保证并联微源输出功率在允许的安全范围内时，其频率与电压符合电能质量的相关要求。同时，虚拟无功-电压控制中加入了功率鲁棒分配控制策略，使虚拟无功的分配不受线路阻抗影响，进而保证并联微源输出功率的合理分配。本文所提出的控制方法在实现低压微网功率解耦控制的同时，保证了良好的电能质量与并联微源功率的合理分配。

1 虚拟功率下垂控制方法

图1为两台逆变器经线路并联的简化示意图，以此来分析逆变器的输出功率与电压及功角的关系。忽略逆变器的输出阻抗，将其等效为理想电压源，iE为其输出电压的有效值，di为其电压超前公共耦合点(Point of Common Coupling, PCC)电压的角度，为线路阻抗，V为PCC处的电压有效值，为并联逆变器的公共负荷，其中i=1,2。

逆变器i的输出功率为

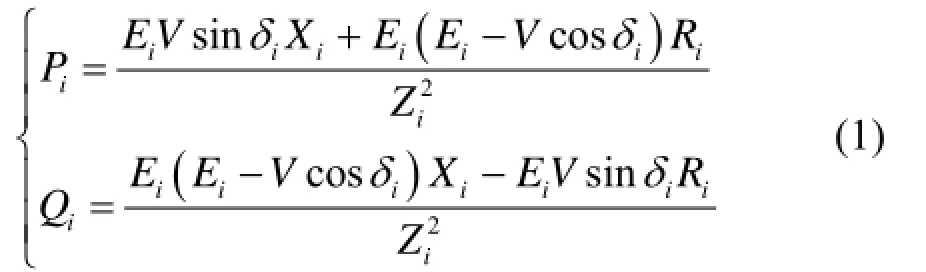
低压微网中线路的电阻和感抗为同一数量级[14]，往往均不可忽略，由式(1)可知，逆变器输出的有功、无功功率均与功角差和电压差都相关，因此传统有功-频率、无功-电压的控制方法在低压微网中直接应用必然会导致有功、无功功率控制的耦合。

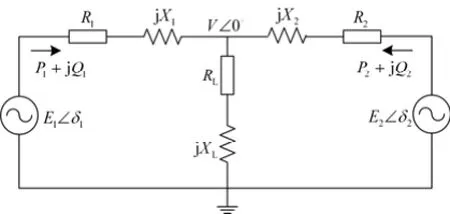
图1 并联逆变器简化模型Fig. 1 Simplified model of parallel inverters

针对低压微网的功率耦合问题，文献[12-13]根据线路阻抗的大小，对功率进行坐标变换，通过引入虚拟功率实现了功率的解耦，坐标变换的实现方式如式(2)所示。

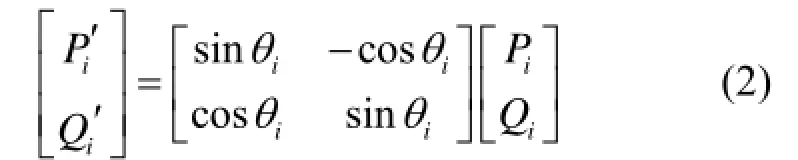
式(2)中， qi满足：定义为变换矩阵，为虚拟有功和虚拟无功功率，将式(1)代入式(2)，并近似认为di较小，即成立，可以得到：

式(3)中，可以近似认为Pi与di、Qi与Ei-V之间呈一一对应关系，因此可以采用虚拟有功-频率、虚拟无功-电压的下垂控制方式以解决由于线路阻抗而引起的功率耦合问题，下垂方程式为

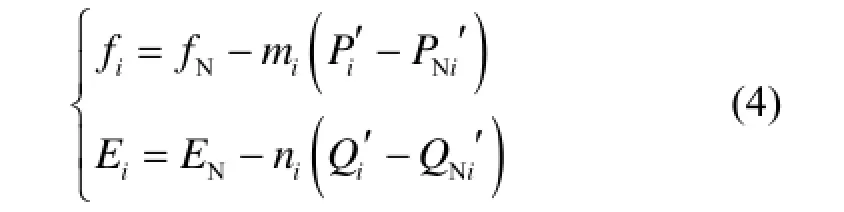
式中：fN、EN为逆变器输出电压的额定频率与有效值；mi、ni为下垂系数；为逆变器的额定虚拟有功与虚拟无功功率。

并联逆变器实现功率解耦控制的同时，必须保证出力的合理分配。采用虚拟功率下垂控制方法后，频率、电压只能起到虚拟功率分配的通信媒介的作用，因而实际功率的合理分配必须借助于虚拟功率来实现。虚拟功率下垂控制的实质是将逆变器的输出功率进行了坐标变换，因而最简单易行的功率控制方式是对并联逆变器进行相同的坐标变换，进而通过控制虚拟功率按逆变器的额定容量成比例分配，即可实现实际功率的合理分配。低压微网线路的电阻一般会大于电抗，但微网中仍存在一些输出端有大电感或者变压器的逆变器，其线路等效阻抗一般呈感性，为了兼顾微网线路阻抗的复杂性，同时考虑到线路精确的阻感比可能难以获取，故选取变换矩阵的阻抗角。

2 新型虚拟功率下垂控制方法

下垂控制的特点是根据负荷需求的变化对逆变器输出电压的频率和幅值进行调整，因此微网孤岛运行时其频率和电压幅值可能会存在一定偏差，严重时可能不满足电能质量的要求。国家《GB/T 15945-2008 电能质量电力系统频率偏差》标准中规定：电力系统正常运行条件下频率偏差限值为当系统容量较小时，偏差限值可以放宽到《GB/T 12325-2008 电能质量供电电压偏差》标准中规定：20 kV及以下三相供电电压偏差为标称电压的 7±%。本文的研究对象为小容量低压微电网，采用380 V三相供电方式，因此微网孤岛运行时的频率偏差不允许超过 0.5± Hz，而电压偏差不允许超过 7±%。

2.1 频率下垂控制方法

设逆变器的额定有功功率为NP、无功功率为0，其安全运行范围为采用阻抗角 45º对功率进行坐标变换，得到变换前后的功率关系如图2所示。

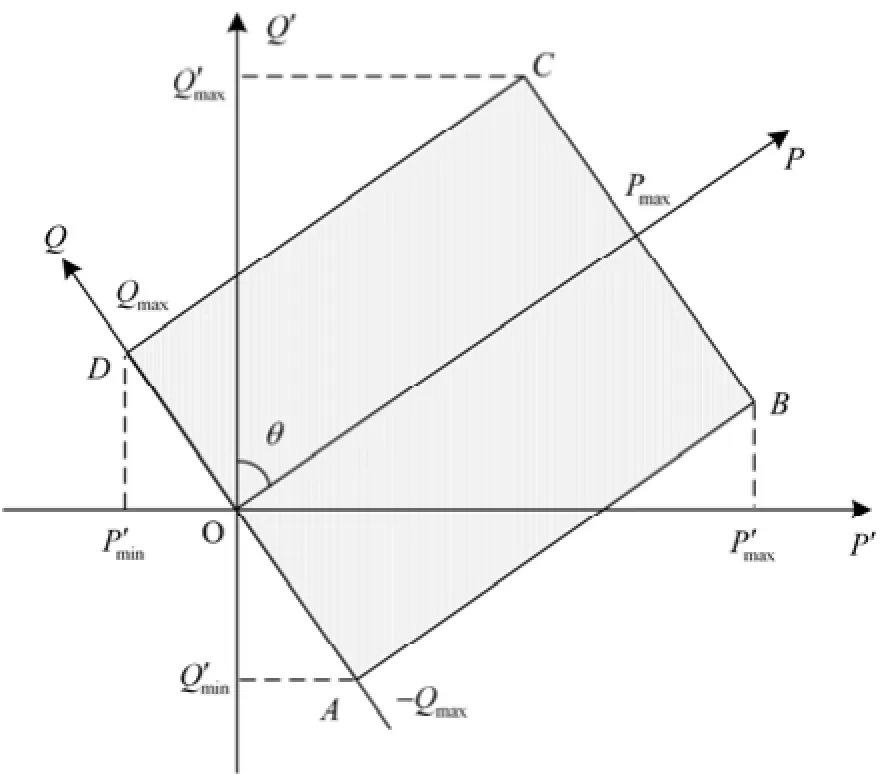
图2 坐标变换示意图Fig. 2 Coordinate transformation scheme

根据图2易得，逆变器的虚拟有功功率范围为

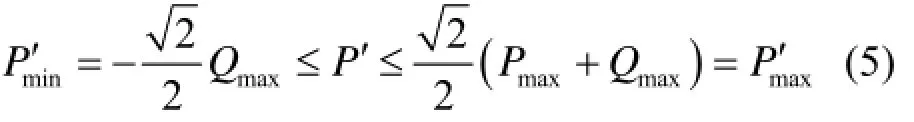
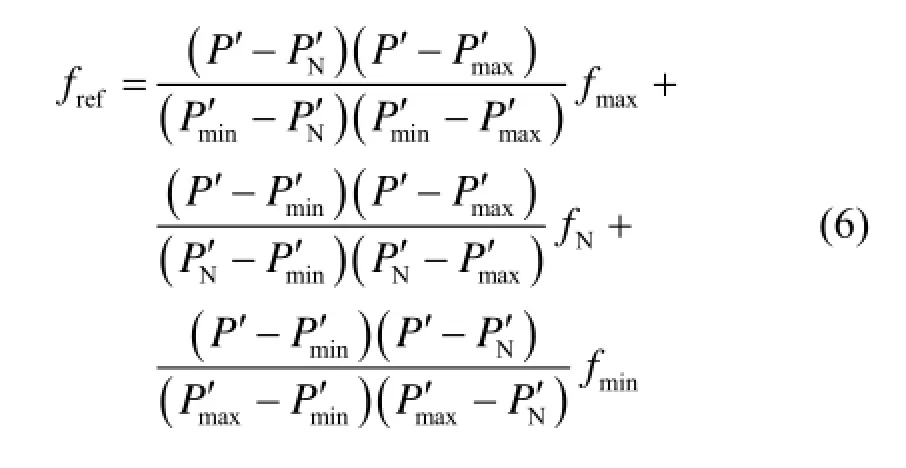
式中，reff 为逆变器电压环频率的给定值。

2.2 电压下垂控制方法及其改进措施

并联系统稳态时的频率处处相等，因此虚拟有功功率可以按逆变器容量成比例分配。如果电压控制采取与频率相同的方法，由于逆变器出口线路的长度与型号等可能不完全相同，导致线路阻抗存在差异，并联逆变器输出电压的幅值稳态时无法保证相等，故虚拟无功功率的合理分配无法保障。由于坐标变换矩阵为非奇异矩阵，因而逆变器实际输出功率的合理分配无法实现。

针对虚拟无功功率的分配问题，本文借鉴文献[15]的并联功率鲁棒控制方法，其通过在电压下垂控制环中增加积分器，实质相当于在逆变器电压电流双闭环控制的基础上，增加了公共耦合点电压的反馈控制，使得下垂控制得到的电压值相当于PCC点电压的给定值。对于并联逆变器而言，PCC点的电压是相同的，稳态时积分器的输入为零，因此各并联逆变器下垂控制得到的电压给定值均等于PCC点的电压，故虚拟无功功率可以实现按容量比例分配，进而可以实现逆变器实际输出有功和无功功率的合理分配。同时，增加PCC点电压反馈之后，电压下垂特性的作用对象是PCC点的电压，当逆变器的虚拟无功功率在范围内时，可以保证PCC处的电压幅值始终满足电能质量要求，避免了线路阻抗上的压降而导致的电压跌落问题。

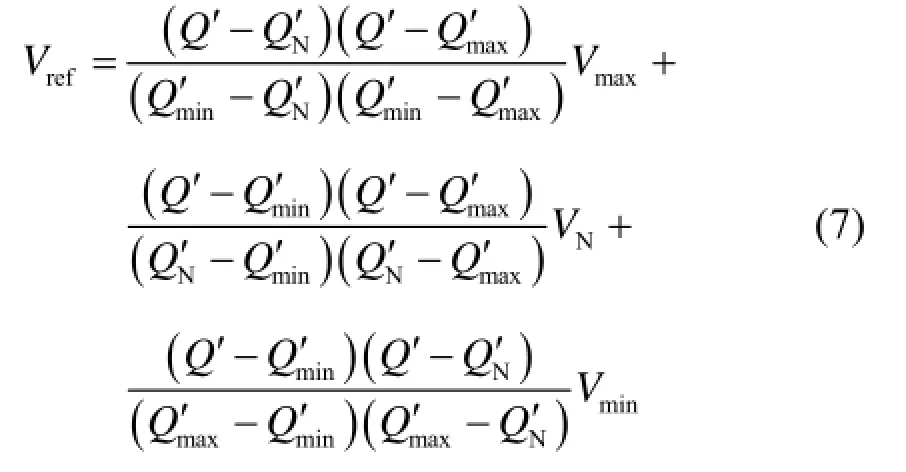
改进后的虚拟无功-电压下垂控制方程式为式中：Vref为PCC处电压的给定值；额定虚拟无功功率为，且Q应满足式(8)的要求。

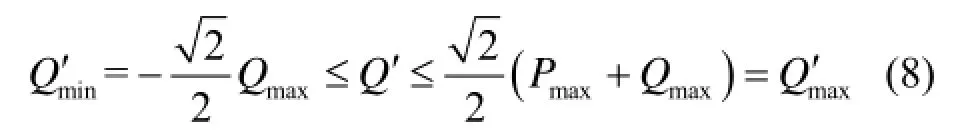
由式(7)得到的 PCC点电压给定值与实际值之差作为积分器的输入，其输出作为逆变器电压环的给定。改进后的虚拟功率下垂控制的整体结构如图3所示。

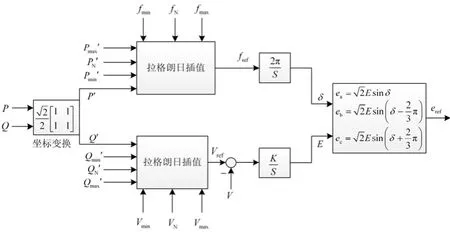
图3 新型虚拟功率下垂控制框图Fig. 3 Block diagram of new virtual power droop control

3 算例分析与仿真验证

为了验证新型虚拟功率下垂控制方法的正确性与有效性，以两台同容量逆变器并联孤岛运行为例搭建了仿真模型，仿真参数如表1所示。

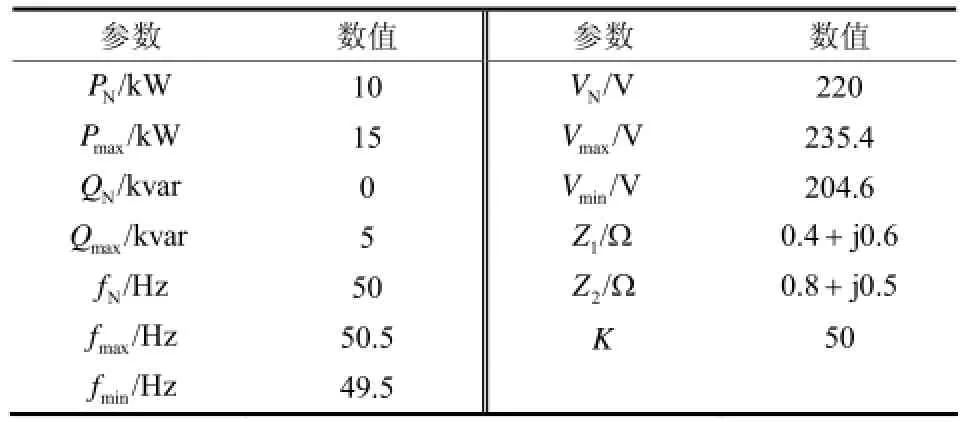
表1 仿真参数Table 1 Simulation parameters

根据表1的数据及虚拟功率与实际功率的转化关系，可得虚拟功率各相关参数如表2所示。

当采用式(4)的固定下垂系数方法时，以虚拟有功-频率控制为例，下垂系数的求解有两种途径，即根据虚拟有功额定值与上限值及其对应的频率求解，或者根据虚拟有功额定值与下限值及其对应的频率求解，以本文参数为例，由两种途径求得的下垂系数m的取值分别如式(9)、式(10)中m1、m2所示。

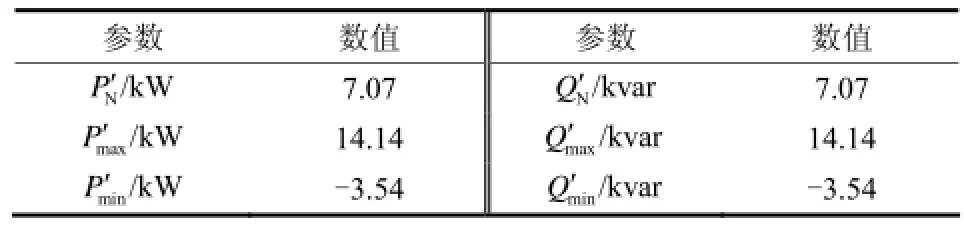
表2 虚拟功率相关参数Table 2 Parameters related to virtual power

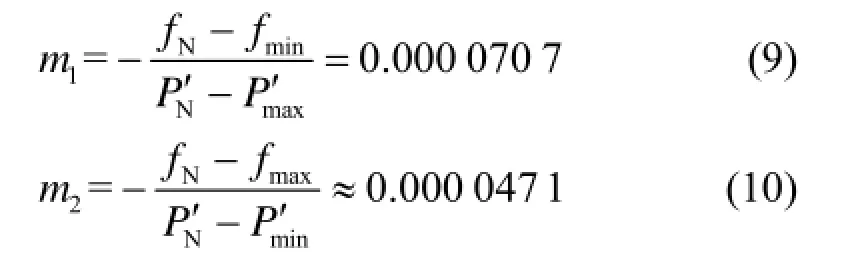
由以上分析可知，通过两种途径求得的下垂系数不相同，当选取m1作为频率下垂系数时，易知当逆变器的虚拟有功功率接近Pmin时，频率会大于此时不符合电能质量要求；当选取m2作为下垂系数时，虽然不会出现频率超出其允许偏差的情况，但其并没有充分利用到频率的可调整范围。

同理，电压下垂系数n的取值也有两种情况，

为了验证本文所提出的下垂控制方法不存在上述提到的基于固定下垂系数的虚拟功率控制方法所存在的问题，利用Matlab/Simulink对两种控制方法进行了仿真验证与结果对比。仿真时间长度为1.8 s，其中0~0.6 s，并联系统的公共负荷为6 kW、8 kvar，0.6~1.2 s之间，系统的负荷为6 kW，1.2 s之后，系统公共负荷变为6 kW、-8 kvar，固定下垂系数选取m10.000 070 7、 n10.00218。图4、图5分别给出了固定下垂系数与本文提出的基于拉格朗日插值的下垂方法的仿真结果。

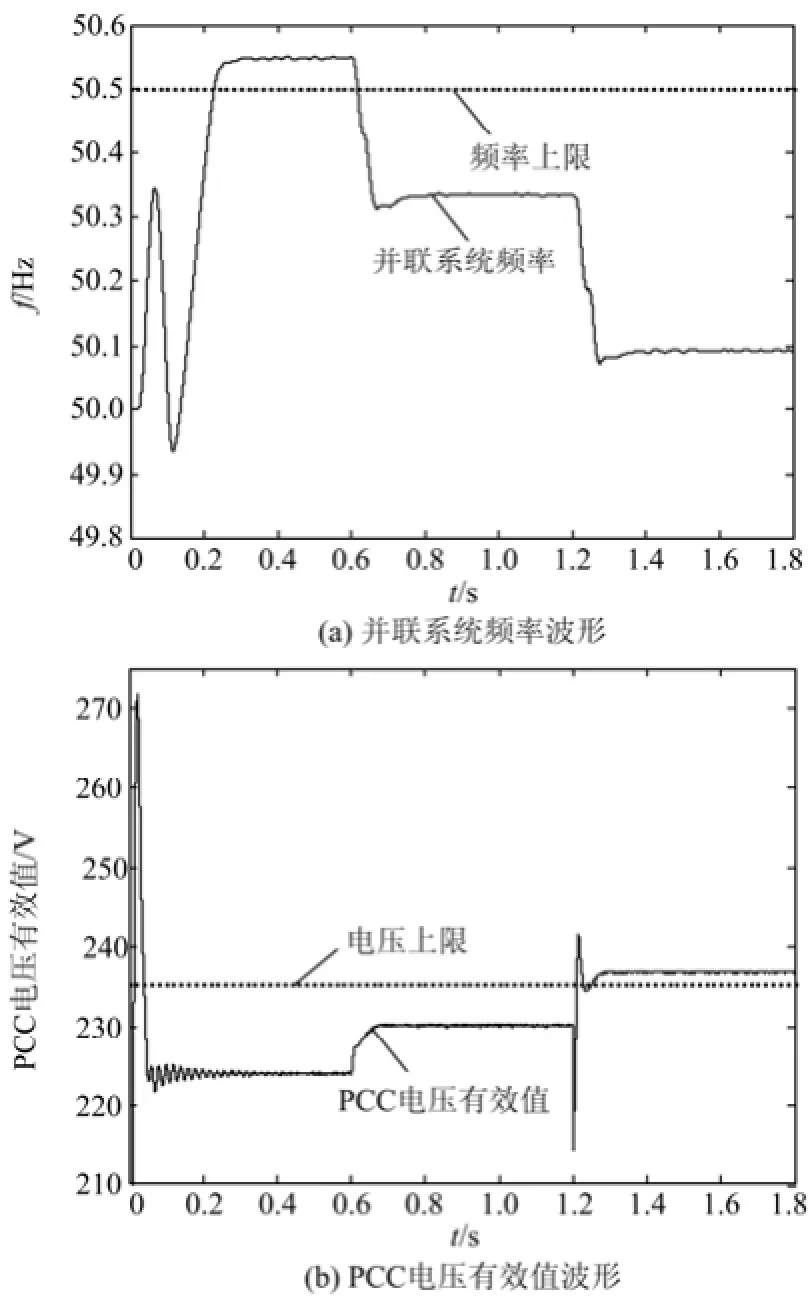
图4 固定下垂系数仿真结果Fig. 4 Simulation results of fixed droop coefficient

仿真条件中设置的负荷大小均在逆变器的允许运行范围之内，但由图4可以看出，由于仿真时选取了频率、电压下垂系数中较大的一组，当并联系统带6 kW、8 kvar负荷时，如图4(a)中0~0.6 s之间所示，系统的稳态频率超出了频率上限50.5 Hz，而当系统带 6 kW、-8 kvar负荷时，如图 4(b)中1.2~1.8 s之间所示，PCC的稳态电压已超出电压上限235.4 V，显然不符合电能质量要求。采用基于拉格朗日插值的虚拟功率下垂控制方法后，由图5(a)、(b)可以看出，相同仿真条件下，系统稳态时的频率与PCC的电压幅值均符合电能质量的要求；且由图5(c)、(d)可以看出，两逆变器稳态时的输出有功和无功功率都可以均分，故本文所提出的新型虚拟功率下垂控制方法可以保障并联逆变器稳态输出功率的合理分配。

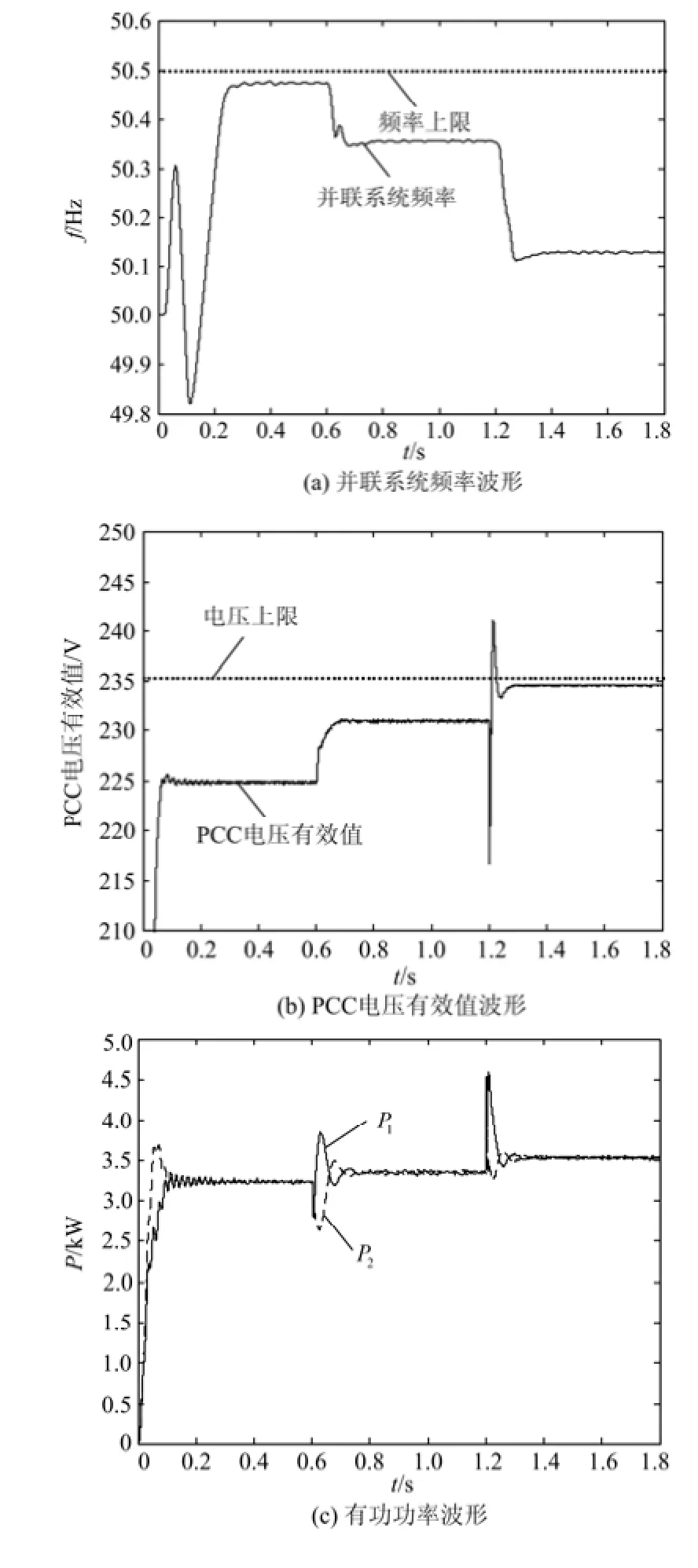
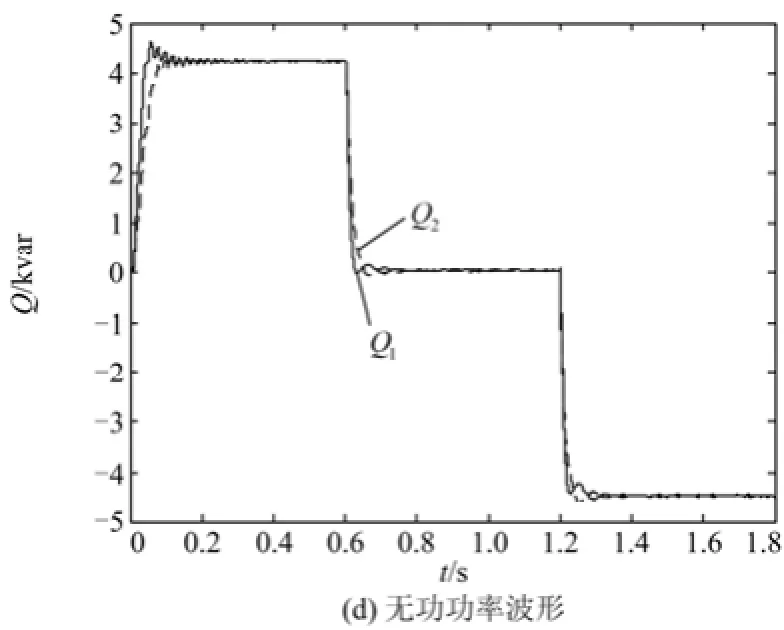
图5 新型下垂控制仿真结果Fig. 5 Simulation results of new droop control

4 结论

本文采用了经过坐标变换的虚拟功率下垂控制方法以实现低压微网的功率解耦控制。在解耦的基础上，为了保障微网孤岛运行时的频率和电压质量，

提出了一种基于拉格朗日插值方法的虚拟功率下垂控制策略，保证当并联微源输出功率在其允许范围内时，系统的频率和电压均符合电能质量的要求。同时，加入了并联功率鲁棒控制方法，保证并联微源可以实现功率的合理分配。仿真结果表明，该方案在实现低压微网功率解耦的基础上，可以保障优质的电能质量和功率的合理分配。

[1] 王成山, 肖朝霞, 王守相. 微网综合控制与分析[J]. 电力系统自动化, 2008, 32(7): 98-103.

WANG Chengshan, XIAO Zhaoxia, WANG Shouxiang. Synthetical control and analysis of microgrid[J]. Automation of Electric Power Systems, 2008, 32(7): 98-103.

[2] 陈娜, 王劲松. 微电网模式控制器研制与应用[J]. 电力系统保护与控制, 2015, 43(11): 115-120.

CHEN Na, WANG Jinsong. Development and application of microgrid’s connect & off-grid device[J]. Power System Protection and Control, 2015, 43(11): 115-120.

[3] 徐玉琴, 马焕均. 基于改进下垂控制的逆变器并联运行技术[J]. 电力系统保护与控制, 2015, 43(7): 103-107.

XU Yuqin, MA Huanjun. Parallel operation technology of inverters based on improved droop control[J]. Power System Protection and Control, 2015, 43(7): 103-107.

[4] 荆龙, 黄杏, 吴学智. 改进型微源下垂控制策略研究[J]. 电工技术学报, 2014, 29(2): 145-152.

JING Long, HUANG Xing, WU Xuezhi. Research on improved microsource droop control method[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 145-152.

[5] 张明锐, 杜志超, 王少波. 微网中下垂控制策略及参数选择研究[J]. 电工技术学报, 2014, 29(2): 136-144.

ZHANG Mingrui, DU Zhichao, WANG Shaobo. Research on droop control strategy and parameters selection of microgrids[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 136-144.

[6] LI Yunwei, KAO Chingnan. An accurate power control strategy for power-electronics-interfaced distributed generation units operating in a low-voltage multibus microgrid[J]. IEEE Transactions on Power Electronics, 2009, 24(12): 2977-2988.

[7] 程军照, 李澍森, 吴在军, 等. 微电网下垂控制中虚拟电抗的功率解耦机理分析[J]. 电力系统自动化, 2012, 36(7): 27-32．

CHENG Junzhao, LI Shusen, WU Zaijun, et al. Analysis of power decoupling mechanism for droop control with virtual inductance in a microgrid[J]. Automation of Electric Power Systems, 2012, 36(7): 27-32.

[8] 闫俊丽, 彭春华, 陈臣. 基于动态虚拟阻抗的低压微电网下垂控制策略[J]. 电力系统保护与控制, 2015, 43(21): 1-6.

YAN Junli, PENG Chunhua, CHEN Chen. Droop control strategy based on dynamic virtual impedance in low-voltage microgrid[J]. Power System Protection and Control, 2015, 43(21): 1-6.

[9] 王成山, 肖朝霞, 王守相. 微网中分布式电源逆变器的多环反馈控制策略[J]. 电工技术学报, 2009, 24(2): 100-107.

WANG Chengshan, XIAO Zhaoxia, WANG Shouxiang. Multiple feedback loop control scheme for inverters of the micro source in microgrids[J]. Transactions of China Electrotechnical Society, 2009, 24(2): 100-107.

[10] 牟晓春, 毕大强, 任先文. 低压微网综合控制策略设计[J]. 电力系统自动化, 2010, 34(19): 91-96.

MOU Xiaochun, BI Daqiang, REN Xianwen. Study on control strategies of a low voltage microgrid[J]. Automationof Electric Power Systems, 2010, 34(19): 91-96.

[11] LI Yan, LI Yunwei. Decoupled power control for an inverter based low voltage microgrid in autonomous operation[C] // Proceedings of the Power Electronics and Motion Control Conference, Wuhan, 2009: 2490-2496.

[12] 周贤正, 荣飞, 吕志鹏, 等. 低压微电网采用坐标旋转的虚拟功率 V/f下垂控制策略[J]. 电力系统自动化, 2012, 36(2): 47-51.

ZHOU Xianzheng, RONG Fei, LÜ Zhipeng, et al. A coordinate rotational transformation based virtual power V/f droop control method for low voltage microgrid[J]. Automation of Electric Power Systems, 2012, 36(2): 47-51.

[13] DE BRABANDERE K, BOLSENS B, VAN DEN KEYBUS J, et al. A voltage and frequency droop control method for parallel inverters[J]. IEEE Transactions on Power Electronics, 2007, 22(4): 1107-1115.

[14] 李鹏, 杨世旺, 王阳, 等. 基于相对增益分析的目标函数对角化微网功率解耦控制方法[J]. 中国电机工程学报, 2014, 34(13): 2039-2046.

LI Peng, YANG Shiwang, WANG Yang, et al. Objective function diagonalization decoupling control of microgrid power based on relative gain analysis[J]. Proceedings of the CSEE, 2014, 34(13): 2039-2046.

[15] 吕志鹏, 罗安. 不同容量微源逆变器并联功率鲁棒控制[J]. 中国电机工程学报, 2012, 32(12): 35-42.

LÜ Zhipeng, LUO An. Robust power control of paralleled micro-source inverters with different power ratings[J]. Proceedings of the CSEE, 2012, 32(12): 35-42.

颜湘武(1965-)，男，博士，教授，博士生导师，研究方向为新能源电力系统与微网技术、现代电力变换、新型储能与节能；E-mail: xiangwuy@ncepu.edu.cn

王星海(1990-)，男，硕士研究生，研究方向为新能源电力系统与微网技术；E-mail: xinghai_neptune@126.com

王月茹(1991-)，女，通信作者，硕士研究生，研究方向为新能源电力系统与微网技术。E-mail: wyr_ncepu@ 126.com

(编辑 魏小丽)

A Lagrange interpolation based virtual power droop control method for microgrid

YAN Xiangwu, WANG Xinghai, WANG Yueru
(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)

In low voltage microgrid, the transmission line is relatively resistive and that is the reason why power coupling problem will be caused when conventional droop control method is adopted. Virtual power droop control method based on coordinate transformation could realize power decoupling control. Aiming at the problem that the frequency and voltage quality of the microgrid in islanding operation cannot be guaranteed by the fixed virtual power droop coefficient, a new virtual power droop control strategy based on Lagrange interpolation is proposed, which could guarantee the frequency and voltage quality while the output power of the inverter is within its allowable range. The robust power allocation method is adopted to achieve reasonable power allocation of parallel inverters, which makes the virtual power distribution not be affected by the line impedance. A parallel model of two inverters with different line impedances using the above strategy and the fixed droop coefficient strategy are simulated respectively. Simulation results indicate that the new droop control method could guarantee good power quality and reasonable power allocation between parallel micro-sources. This work is supported by National High-tech R & D Program of China (863 Program) (No. 2015AA050603).

microgrid; power coupling; virtual power; Lagrange interpolation; power quality; power allocation

2015-10-28；

2016-01-22作者简介：

10.7667/PSPC151901

国家高技术研究发展计划(863计划) (2015AA050603)；河北省科技计划项目(15214307D)；河北省自然科学基金项目(E2015502046)；国家电网公司科学技术项目(SGTYHT/14-JS-188)