考虑大规模电动汽车接入电网的双层优化调度策略

胡文平，何立夫，陈杰军，于腾凯，孟 良

考虑大规模电动汽车接入电网的双层优化调度策略

胡文平1，何立夫2，陈杰军3，于腾凯1，孟 良1

(1.国网河北省电力公司电力科学研究院，河北 石家庄 050021；2.国网湖南省电力公司防灾减灾中心，湖南 长沙 410129；3.武汉大学电气工程学院，湖北 武汉 430072)

随着经济发展和化石燃料短缺、环境污染严重的矛盾日益尖锐，电动汽车(Electric Vehicle, EV)的发展和普及将成为必然趋势。大规模无序充电的电动汽车接入电网充电将给电网带来强大的冲击，并可能导致电网局部过负荷，威胁电网运行的安全性和经济性。因此研究了发电机、电动汽车、风力的协同优化计划问题，提出了一种基于输电和配电系统层面的电动汽车充放电计划双层优化调度策略。在输电网层，以减少发电机组的运行成本、PM2.5排放量、用户的总充电成本和弃风电量为目标，建立了基于机组最优组合的上层优化调度模型；在配电网层，以降低网损为目标，考虑网络安全约束和电动汽车的空间迁移特性，建立了基于最优潮流的下层优化调度模型。在基于标准10机输电网和IEEE33节点配电网的电力系统仿真模型上，对所提的基于双层优化的大规模电动汽车充放电调度策略进行了仿真分析，验证了所提双层优化调度策略的有效性和优越性。

电动汽车；双层优化充放电策略；机组组合；最优潮流

0 引言

截至2015年8月底，我国电动汽车保有量达到22.30万辆，国家明确提出到2020年电动汽车保有量达到500万辆。由于大多数用户生活作息习惯和驾驶习惯的相近，规模化的电动汽车无序充电行为将可能出现集中化现象，给电网造成不可估量的影响。风能由于清洁、可再生的特点发展很快，但是风电场的接入对电网存在不利影响[1]。采用合理的电动汽车优化调度策略，规划电动汽车有序充电行为，可有效解决电动汽车随机充电行为对电网的不利影响，提高新能源利用率。因此研究大规模接入电网的电动汽车优化调度策略具有重要意义。

文献[2-4]在低压配电网中研究电动汽车的充电策略，没有考虑与输电网侧发电机组的协调。在输电网层面上，也有人对电动汽车与发电机组的协调优化做了不少研究。文献[5-8]以机组的运行成本和CO2排放量最小为优化目标，研究了考虑电动汽车充电和放电的机组组合问题，研究发现通过充放电电动汽车能平滑负荷曲线，能降低电力系统对小而昂贵的小发电机组的依赖，因而能够减少机组的运行成本和CO2的排放量。基于双层优化的电动汽车充放电调度策略出现了一些报道。文献[9]提出了一种基于计及安全约束的机组组合的电动汽车优化调度方法，并建立了两阶段模型：子模型1即为机组最优组合模型，能够获得各时段最优充放电的电动汽车数量，子模型2在考虑交流潮流约束的情况下将各时段最优充放电的电动汽车数量合理的配到电网的各个节点上，其研究模型是针对输电网络，但在输电网络中，各个节点的电动汽车数量是相对固定的，可调度性较差。文献[10-11]建立了双层经济调度的电动汽车充放电调度模型，内层为最优潮流模型，优化电动汽车充放电负荷的时间分布特性，外层模型能优化出了电动汽车充放电负荷的最优空间分布，但其在考虑充放电负荷的空间分布时没有考虑电动汽车在电网节点中的流动性，其研究模型也仅针对输电网络。文献[12-13]分别研究了电动汽车有序充电的时间调度、空间调度和时空联合调度，其时空联合调度策略能够优化换电站的充电负荷在时间上和空间上的分布，但由于其决策矩阵能够指出具体的电动汽车去具体的换电站进行充电，当电动汽车和换电站的规模很大时，其优化算法的性能难以保证。文献[14-15]对电动汽车的充放电进行分层分区调度，在上层调度中，对电力系统和各电动汽车代理商进行协调优化，以负荷波动最小为目标，分配各代理商各时段的充放电负荷；在下层调度中，各代理商对管辖的电动汽车各时段的充放电状态进行控制，完成调度任务。

上述基于双层优化的电动汽车充电策略是单独在输电网层或配电网层对时间和空间两个维度上进行优化调度，而根据文献[16]的研究发现，有必要同时在输电网层和配电网层进行电动汽车充电策略的优化。因此本文提出了一种基于双层优化的电动汽车充放电调度策略，该双层优化调度策略在输电网层对电动汽车和发电机组、新能源进行时间维度上的优化，在配电网层考虑电动汽车的流动性对充放电负荷进行空间位置的优化。本文假设电动汽车充放电行为完全服从电网调度。

1 基于双层优化的电动汽车充放电调度策略

1.1 上层优化调度策略建模

考虑到风电的波动性和不确定性，本文采用了基于场景分析的方法来描述风电的波动性和不确定性。在输电系统层面上，为使电动汽车的充放电负荷在时间上能与发电机组的出力、风电出力相协调以达到最优的效果，提出了基于日前机组组合模型的上层调度策略，其优化变量为各个时段中机组的启停状态及其出力、充放电的电动汽车数量和弃风电量。基于机组组合的上层优化调度策略的建模过程如下。

1.1.1 目标函数

上层优化的目标是使得电动汽车的充放电负荷与发电机组出力、风电出力相协调，提升整体的经济性，所以上层优化策略应该要能降低发电机组的运行成本，减少污染物的排放，尽量消纳更多的风电，减少电动汽车车主的充电成本等。所以目标函数应该包括机组运行的燃料成本[17-18]、开停机成本[19]、污染物排放惩罚成本、车主的充电成本、弃风的惩罚成本等几部分。

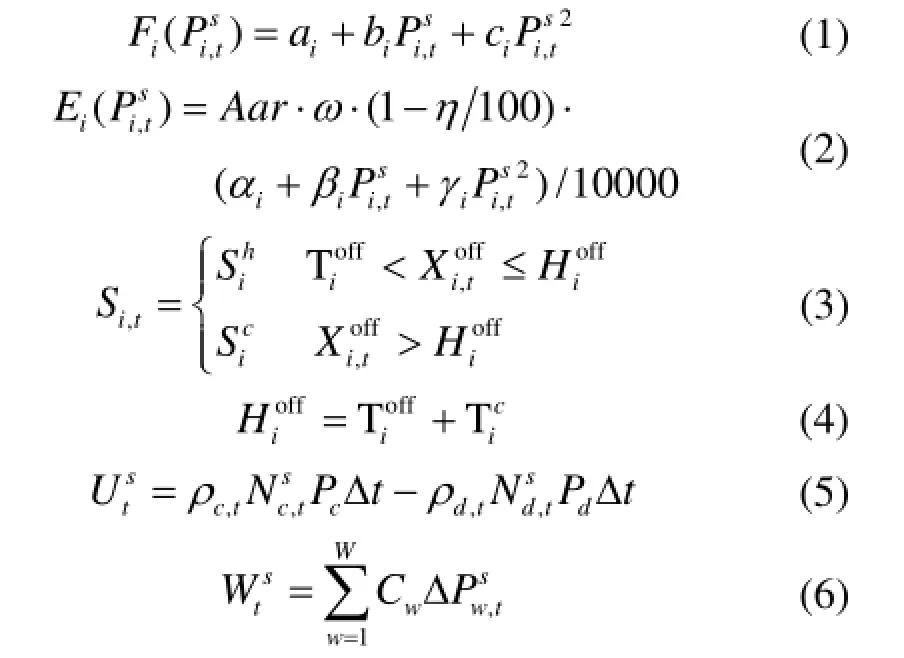
式(1)~式(6)分别表示机组的燃料成本、PM2.5排放量惩罚成本、启动成本、停机成本、用户充电成本和弃风成本。其中为场景s下发电机组i在时段t的燃料成本；ia,ib和ic为机组i的燃料成本特性曲线系数，是在场景s下发电机i组在时段t输出的有功功率。为场景s下发电机组i在时段t的PM2.5排放量；Aar为平均燃煤收到基灰分(%)，计算时，其默认值取20；w为燃煤灰分至PM2.5的转化系数(%)，计算时，其默认值取5.1；h控制措施对PM2.5的去除效率(%)，计算时，其默认值取99[20-21]；PM2.5的排放量正比于煤耗量，为机组i的煤耗特性曲线系数。,itS 为发电机组i在时段t的启动成本；为发电机组i的热启动成本；为发电机组i的冷启动成本；为发电机组i在时段t之前的连续停机时间；为机组i热启动和冷启动的过渡时间；为发电机组i的最小允许停机时间；为发电机组i的冷启动时间。在标准系统中，火电机组的停机成本为常数且通常为0[22]。为场景s下在时段t的车主总充电成本；为时段t的电动汽车的充电价格，为时段t的电动汽车的放电价格；为场景s下在时段t充电的电动汽车总数量；Pc为电动汽车的平均充电功率；为场景s下在时段t放电的电动汽车总数量；Pd为电动汽车的平均放电功率；为时段t的时长，本文中其取值为 1。为场景s下在时段t的弃风惩罚成本；W为风电场数目；Cw为弃风惩罚价格；为场景s下风电场w在时段t的弃风电量。

在进行机组开停机序列决策时，以机组的启停成本最小为目标；在进行由风电场景驱动的在线机组的运行基点决策时，以所有场景的期望成本最小为目标。总的目标函数可表述为

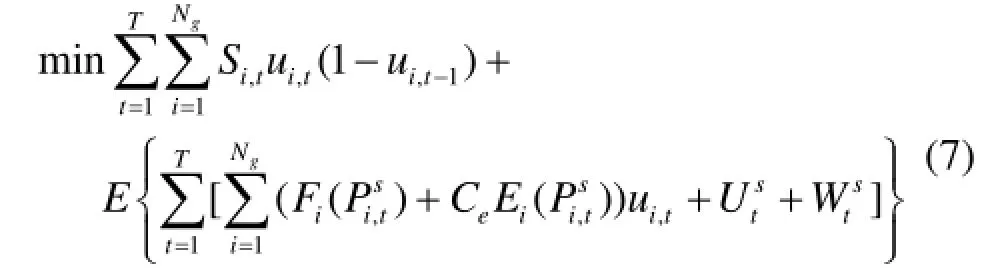
式中：T为总优化时段数；Ng为发电机组总台数；为火电机组i在时段t的启停成本函数；发电机组i在时段t的运行状态，1表示运行，0表示停机；为求所有场景的数学期望；Prs为风电场景s出现的概率；为火电机组i的燃料成本函数；为场景s下发电机组i在时段t的有功出力；为火电机组i的PM2.5排放量；为 PM2.5排放惩罚价格因子；为场景s下电动汽车车主在时段t的总充电成本；为场景s下风电场在时段t的总弃风惩罚成本。

1.1.2 约束条件

下列约束条件在每个时段t都必须满足。

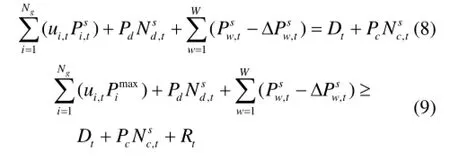
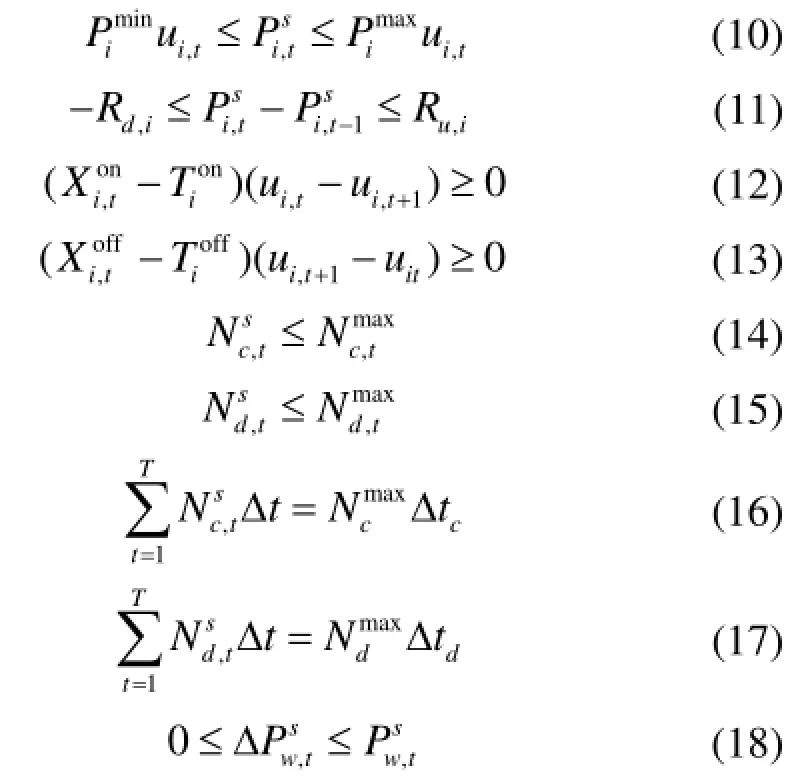
式(8)表示系统功率平衡约束，式(9)~式(11)分别表示系统的旋转备用约束、机组出力约束和爬坡约束。式(12)、式(13)表示机组最小开停机时间约束。式(14)、式(15)表示可充放电的电动汽车数量约束。式(16)、式(17)是充放电需求约束。式(18)表示弃风电量约束。其中，Dt为时段t系统总的基本负荷；为场景s下风电场w在时段t的预测风电功率。其中，为发电机组i的有功出力上限；Rt为时段t的系统旋转备用需求。为发电机组i的最小有功出力。Ru,i为机组i在单个时段内最大上调有功量；Rd,i为机组i在单个时段内最大下调有功量。为发电机组i在时段t之前处于运行状态的时间；发电机组i在时段t之前处于停机状态的时间；为发电机组i的最小允许运行时间；为发电机组i的最小允许停机时间。为t时段可充电的电动汽车最大数量；为t时段可放电的电动汽车最大数量。为一天中所有可充电的电动汽车总数；ctD 为平均充电时长；为一天中所有可放电的电动汽车总数；dtD 为平均放电时长。为弃风电量；为预测的风电功率。

1.2 下层优化调度策略建模

上层优化策略决定了输电网层的机组出力、风电出力和电动汽车总的充放电负荷曲线，配电网层就需要根据输电网的供电情况和电动汽车在配电网中的空间位置分布来将电动汽车总的充放电负荷最优的分配到配电网中的各个节点上。所以本文在配电网层面提出了基于最优潮流的下层优化调度策略，通过优化潮流分布，将电动汽车的总充放电负荷最优分配到配网的各个节点上，其优化变量为各个时段中各个节点的充放电电动汽车数量。

1.2.1 目标函数

通常配网运营商希望将电动汽车的充放电负荷分配在最合适的节点上以改善配电网的潮流分布，降低配电网的总网损[23]。所以下层优化调度模型以降低配电网的总网损为优化目标，将电动汽车充放电负荷最优分配在配网的节点上。下层优化调度策略的目标函数可以表示为

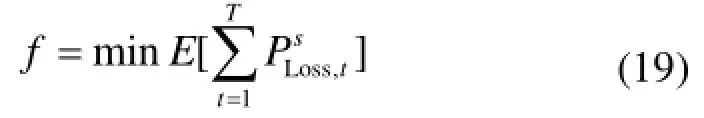
1.2.2 约束条件

下列约束条件在每个时段t都必须满足。为求所有场景的期望值；

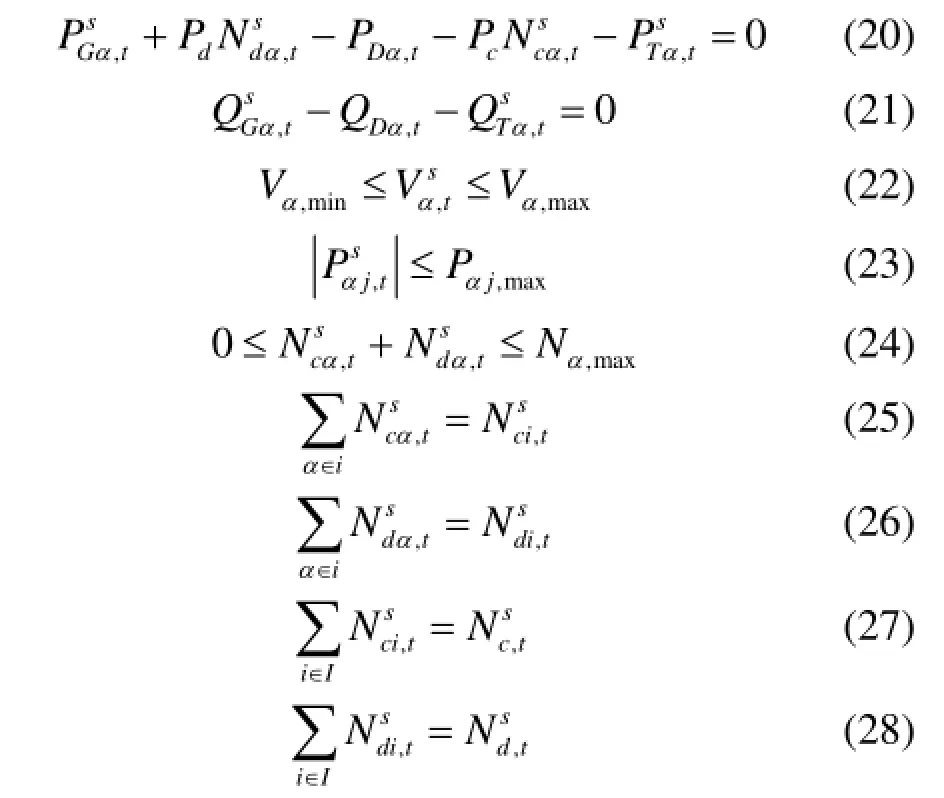
式(20)、式(21)表示节点功率平衡约束；式(22)是节点电压幅值约束；式(23)表示节点电压幅值约束；式(24)是节点充电容量约束；式(25)、式(26)表示区域电动汽车数量约束；式(27)、式(28)是上层调度计划约束。其中，为场景s下节点的有功电源在时段t发出的有功功率；为节点在时段t的有功负荷；为场景s下在时段t在节点充电的电动汽车数量；为场景s下在时段t在节点放电的电动汽车数量；Pc为电动汽车的平均充电功率；Pd为电动汽车的平均放电功率；为场景s下节点的无功电源在时段t发出的无功功率；为节点在时段t的无功负荷；为场景s下在时段t节点传送出去的有功功率；为场景s下在时段t节点传送出去的无功功率；K为配电网中除平衡节点外的节点集合。和分别为节点的电压允许最大值和最小值。为节点和节点j之间的线路可传输最大功率；K为节点和节点j之间的线路在场景s下在时段t传输的有功功率。

2 案例仿真

为了验证所提的基于双层优化的电动汽车充放电调度策略的可行性和有效性，本节构建了一个包含火电机组、风电场、输电网络、配电网络和电动汽车的电力系统仿真模型，如图1所示。

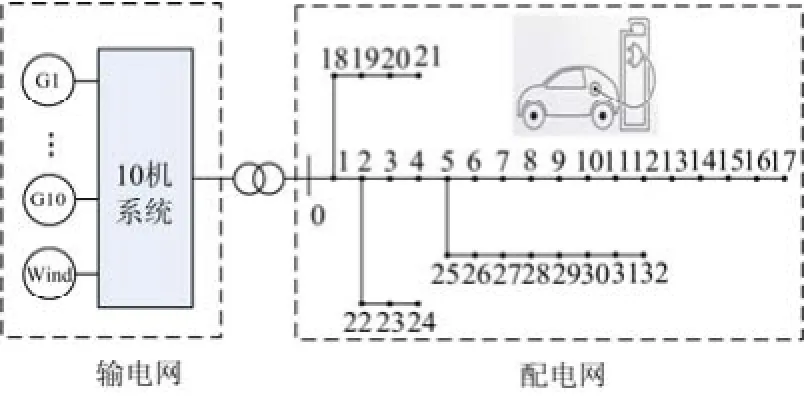
图1 包含输电网络和配电网络的电力系统仿真模型Fig. 1 Simulation model of power system including transmission network and distribution network

2.1 输电网层的仿真分析

假设输电网中含有150 000辆电动汽车，并比较了两种不同电价模式的仿真结果。

算例一：输电网中不含电动汽车。

算例二：电动汽车的充放电电价如图2(a)所示。

算例三：电动汽车充放电电价如图2(b)所示。

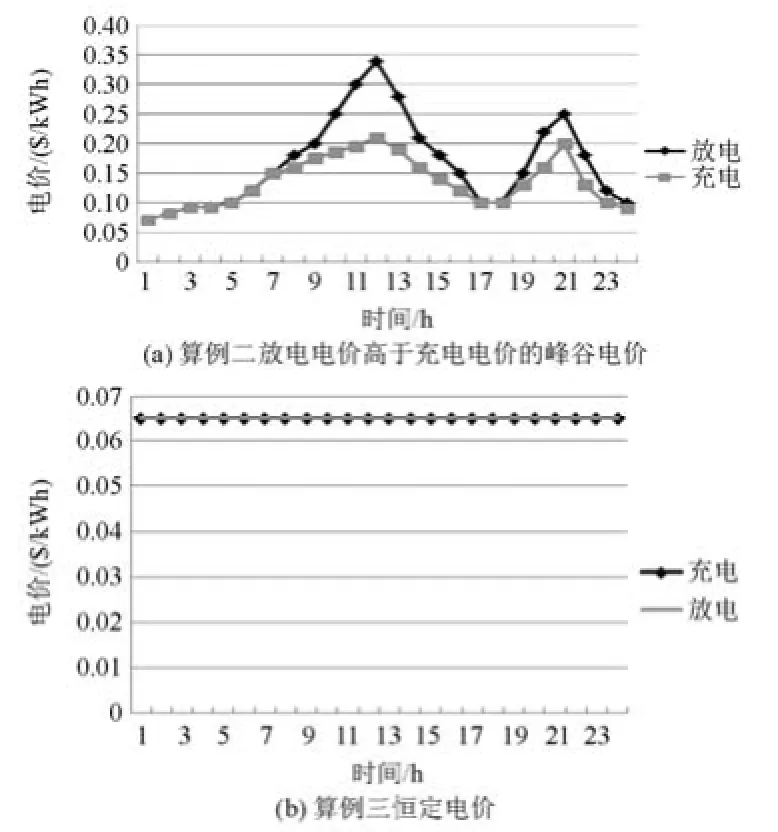
图2 电动汽车充放电电价曲线Fig. 2 Price profiles of charging and discharging

将2.1节中的上层优化调度策略模型线性化后，用AIMMS进行求解。上述2个算例的目标函数值和目标函数中的燃料费用、PM2.5排放量、启动成本、电力系统的运行成本、车主的充电成本、弃风电量的期望值见表 1。与算例一和算例三相比，算例二的总目标函数值明显减小。其中算例二、三电动汽车充放电数量分布如图3所示，可以看出电动汽车充电集中在充电价格较低时刻，放电集中在放电价格较高时刻。

2.2 配电网层的仿真分析

下层优化优化调度策略在IEEE 33节点的配电网络层进行仿真验证。为了便于研究电动汽车的迁移特性对配电网的影响，将配电网分成了居民区、商业区和办公区3个功能区，70%的电动汽车属于居民区，20%的电动汽车属于商业区，10%的电动汽车属于办公区。当考虑到电动汽车的迁移时，在白天大部分的电动汽车停留在办公区和商业区，在晚上大部分的电动汽车停留在居民区。假设在早上上班时间，居民区中80%的电动汽车将迁移到办公区，15%的电动汽车将迁移到商业区；在傍晚下班时间，这些从居民区迁出的电动汽车将会回到居民区，其他的车辆不会驶出其所属于的区域。

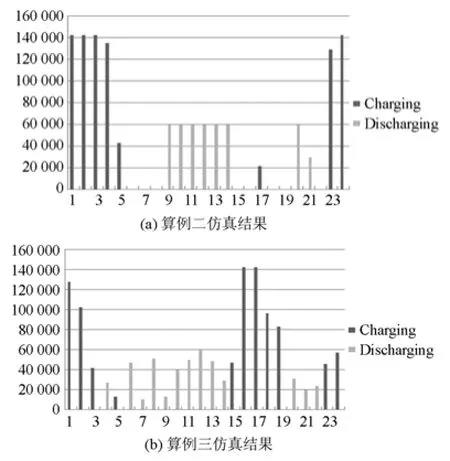
图3 电动汽车充放电数量分布Fig. 3 Scheduling of charging and discharging of different cases

表 1 不同算例的目标函数值Table 1 Objective function results of different cases

算例四：基于输电网层的算例一，配电网中也没有电动汽车。

算例五：基于输电网层的算例二，配电网的分区和电动汽车的迁移特性上所述。

算例五电动汽车充电放电负荷在配电网中的分布如图4所示，本文给出算例五某一时刻电动汽车充电放电负荷在配电网中的分布如图5所示。算例四和算例五的网络损耗如图6所示，算例四和算例五配电网总网损耗分别为2.496 4 MW和2.389 8 MW，算例五的总网损耗比算例四小，这说明通过调度电动汽车在特定位置进行充放电可以优化系统潮流，减少系统网络损耗。

另外，通过图5和图6还可以发现，将配电网中的电动汽车调度到尽量靠近配电网首端的节点充电，到尽量靠近配电网末端的节点放电，能够减少配电网的总网损，提高配电网运行的经济性。在实际规划中，应将充电站尽可能建在靠近配网首末端的位置，并通过相应的差异化电价机制，运用弹性系数法分析用户对电价的响应程度，来引导电动汽车到靠近首端充电站充电，到靠近末端充电站放电。

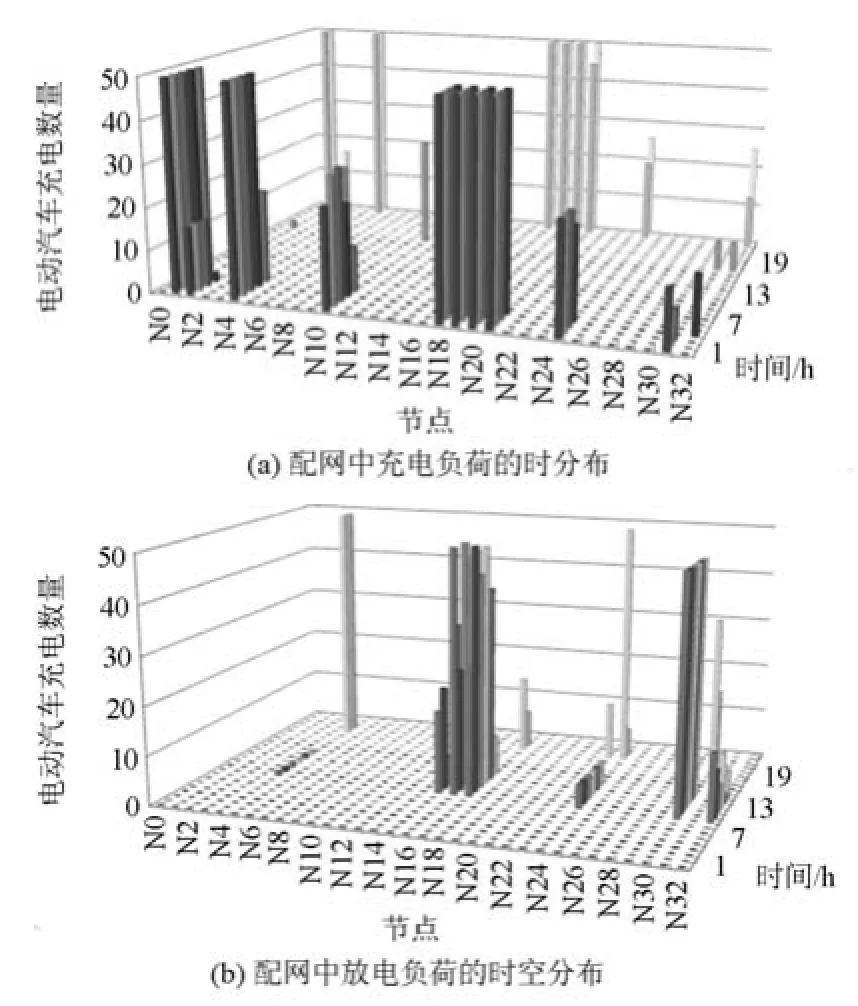
图4 算例五的电动汽车充放电调度结果Fig. 4 Result of EVs charging and discharging scheduling in case 5

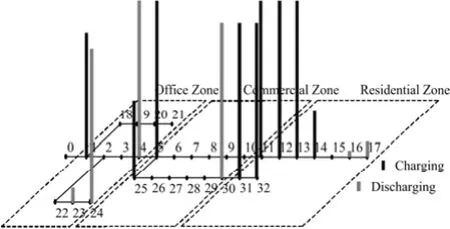
图5 算例五电动汽车充放电负荷在配电网中的分布Fig. 5 Schematic of charging and discharging in the network in case 5

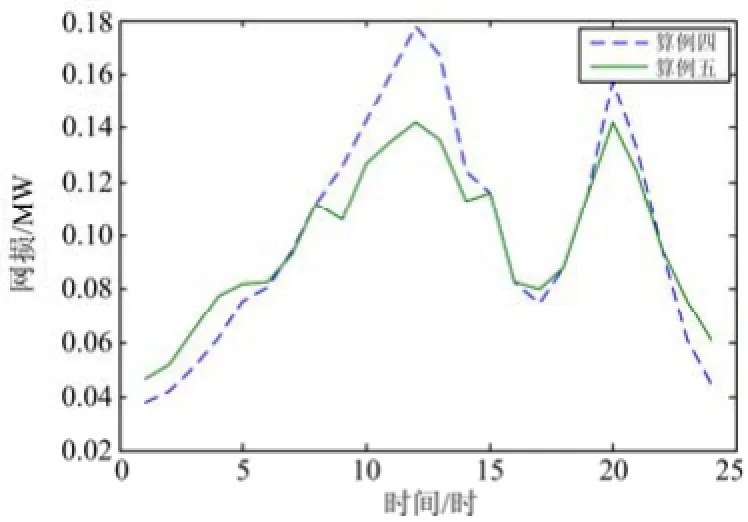
图6 配电网的总网损曲线Fig. 6 Network loss curve

3 总结

为了使电动汽车能与电源端进行协调优化，本文提出了基于双层优化的电动汽车充放电调度策略，该调度策略能分别从输电网层和配电网层对电动汽车的充放电进行协调优化。在输电网层，建立了基于随机机组组合模型的上层优化调度策略模型。上层优化调度策略优化出了各时段的机组启停状态和出力、消纳的风电功率和电动汽车充放电负荷。在配电网层，提出了基于最优潮流的下层优化调度策略。下层优化调度策略以提高配电网运行经济性为目标，根据上层调度策略优化出的结果，考虑电动汽车的空间分布特性，将各时段的电动汽车总充放电负荷优化的分配到配电网的各个节点上。

最后基于标准的10机系统和IEEE33节点构建了一个电力系统仿真平台，应用AIMMS优化软件，对所提的基于双层优化的大规模电动汽车充放电调度策略进行了仿真分析。输电层研究了两种不同的电动汽车充放电电价模式对输电网的影响，分析结论显示恒定的电价模式无法引导电动汽车车主的充放电行为，反应负荷波动的峰谷电价才能引导车主在负荷低谷时充电。配电层研究了功能区划分和电动汽车的迁移特性对配电网运行的影响，仿真结果表明，为了提高配电网运行的经济性，配电网中的电动汽车将被调度到尽量靠近配电网首端的节点进行充电，而到尽量靠近配电网末端的节点进行放电,这样能减少配电网总网损。

虽然本文中假设电动汽车充放电行为完全服从电网调度的这一前提不完全符合实际情况，但未来采取了相应的价格激励等措施后，对电动汽车进行智能引导，可以认为大部分的电动汽车会按电网需求进行优化充电，意味着能够间接的把大部分电动汽车充放电负荷主动分配到配电网的各个节点上。针对电动汽车对于智能引导措施的响应问题，将是下一步工作的重点。

[1] 马玲玲, 杨军, 付聪, 等. 电动汽车充放电对电网影响研究综述[J]. 电力系统保护与控制, 2013, 41(3): 140-148.

MA Lingling, YANG Jun, FU Cong, et al. Review on impact of electric car charging and discharging on power grid[J]. Power System Protection and Control, 2013, 41(3): 140-148.

[2] 党杰, 汤奕, 宁佳, 等. 基于用户意愿和出行规律的电动汽车充电负荷分配策略[J]. 电力系统保护与控制, 2015, 43(16): 8-15.

DANG Jie, TANG Yi, NING Jia, et al. Research on relaying technologies of distribution network including mass electric vehicles grid[J]. Power System Protection and Control, 2015, 43(16): 8-15.

[3] 佟晶晶, 温俊强, 王丹, 等. 基于分时电价的电动汽车多目标优化充电策略[J]. 电力系统保护与控制, 2016, 44(1): 17-23.

TONG Jingjing, WEN Junqiang, WANG Dan, et al. Multi-objective optimization charging strategy for plug-in electric vehicles based on time-of-use price[J]. Power System Protection and Control, 2016, 44(1): 17-23.

[4] 汪春, 吴可, 张祥文, 等. 规模化电动汽车和风电协同调度的机组组合问题研究[J]. 电力系统保护与控制, 2015, 43(11): 41-48.

WANG Chun, WU Ke, ZHANG Xiangwen, et al. Unit commitment considering coordinated dispatch of large scale electric vehicles and wind power generation[J]. Power System Protection and Control, 2015, 43(11): 41-48.

[5] 薛松, 袁越, 傅质馨, 等. 考虑电动汽车入网技术的电力系统机组组合研究[J]. 电力系统保护与控制, 2013, 41(10): 86-92.

XUE Song, YUAN Yue, FU Zhixin, et al. Unit commitment in power system considering vehicle-togrid[J]. Power System Protection and Control, 2013, 41(10): 86-92.

[6] SANDSTORM O, BINDING C. Flexible charging optimization for electric vehicles considering distribution grid constraints[J]. IEEE Transactions on Smart Grid, 2012, 3(1): 26-37.

[7] METS K, VERSCHUEREN T, HAERICK W, et al. Optimizing smart energy control strategies for plug-in hybrid electric vehicle charging[C] // Network Operations and Management Symposium Workshops (NOMS Wksps), 2010 IEEE/IFIP. IEEE, 2010: 293-299.

[8] YANG J, HE L, FU S. An improved PSO-based charging strategy of electric vehicles in electrical distribution grid[J]. Applied Energy, 2014, 128: 82-92.

[9] SORTOMME E, HINDI M, MACPHERSON S D J, et al. Coordinated charging of plug-in hybrid electric vehicles to minimize distribution system losses[J]. IEEE Transactions on Smart Grid, 2011, 2(1): 198-205.

[10] 张谦, 刘超, 周林, 等. 计及可入网电动汽车最优时空分布的双层经济调度模型[J]. 电力系统自动化, 2014, 38(20): 40-45.

ZHANG Qian, LIU Chao, ZHOU Lin, et al. A bi-level economy dispatch model considering temporal and spatial optimal distribution of electric vehicles[J]. Automation of Electric Power Systems, 2014, 38(20): 40-45.

[11] 刘超. 计及电动汽车最优时空分布的分级调度模型研究[D]. 重庆: 重庆大学, 2014.

LIU Chao. A hierarchical dispatching model considering temporal and spatial optimal distribution of electric vehicles[J]. Chongqing: Chongqing University, 2014.

[12] 田文奇, 和敬涵, 姜久春, 等. 电动汽车充电负荷空间分配优化算法[J]. 电工技术学报, 2013, 28(3): 269-276.

TIAN Wenqi, HE Jinghan, JIANG Jiuchun, et al. Electric vehicle charging load spatial allocation optimization algorithm[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 269-276.

[13] 田文奇. 基于时空双尺度的电动汽车换电站有序充电调度方法[D]. 北京: 北京交通大学, 2013.

TIAN Wenqi. Electric vehicle battery swapping station coordinated charging dispatch method based on temporal and spatial double dimensions[D]. Beijing: Beijing Jiaotong University, 2013.

[14] 姚伟锋, 赵俊华, 文福拴, 等. 基于双层优化的电动汽车充放电调度策略[J]. 电力系统自动化, 2012, 36(11): 30-37.

YAO Weifeng, ZHAO Junhua, WEN Fushuan, et al. A charging and discharging dispatching strategy for electric vehicles based on bi-level optimization[J]. Automation of Electric Power Systems, 2012, 36(11): 30-37.

[15] 熊脶成. 基于多尺度空间层次聚类的电动汽车充放电优化调度[D]. 长沙: 长沙理工大学, 2013.

XIONG Luocheng. Charging and discharging optimal scheduling of EVs based on SSHC[D]. Changsha: Changsha University of Science & Technology, 2013.

[16] ORTEGA-VAZQUEZ M A, BOUFFARD F, SILVA V. Electric vehicle aggregator/system operator coordination for charging scheduling and services procurement[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1806-1815.

[17] JING Z X, SHAO W Y, HE X Y, et al. Research on unit commitment in power system with electric vehicles classification[C] // Power and Energy Society General Meeting (PES), 2013 IEEE. IEEE, 2013: 1-5.

[18] 陆凌蓉, 文福拴, 薛禹胜, 等. 计及可入网电动汽车的电力系统机组最优组合[J]. 电力系统自动化, 2011, 35(21): 16-20.

LU Lingrong, WEN Fushuan, XUE Yusheng, et al. Unit commitment in power systems with plug-in electric vehicles[J]. Automation of Electric Power Systems, 2011, 35(21): 16-20.

[19] SABER A, VENAYAGAMOORTHY G K. Intelligent unit commitment with vehicle-to-grid a cost-emission optimization[J]. Journal of Power Sources, 2010, 195(3): 898-911.

[20] SABER A Y, VENAYAGAMOORTHY G K. Optimization of vehicle-to-grid scheduling in constrained parking lots[C] // Power & Energy Society General Meeting, 2009. PES'09. IEEE. IEEE, 2009: 1-8.

[21] SABER A Y, VENAYAGAMOORTHY G K. Unit commitment with vehicle-to-grid using particle swarm optimization[C] // PowerTech, 2009 IEEE Bucharest. IEEE, 2009: 1-8.

[22] SABER A, VENAYAGAMOORTHY G K. Resource scheduling under uncertainty in a smart grid with renewables and plug-in vehicles[J]. IEEE Systems Journal, 2012, 6(1): 103-109.

[23] GHANBARZADEH T, GOLEIJANI S, MOGHADDAM M P. Reliability constrained unit commitment with electric vehicle to grid using hybrid particle swarm optimization and ant colony optimization[C] // Power and Energy Society General Meeting, 2011 IEEE. IEEE, 2011: 1-7.

A bi-layer optimization based schedule considering large-scale electric vehicles

HU Wenping1, HE Lifu2, CHEN Jiejun3, YU Tengkai1, MENG Liang1
(1. State Grid Hebei Electric Power Research Institute, Shijiazhuang 050021, China; 2. State Grid Hunan Electric Power Company and Reduction Center, Changsha 410129, China; 3. School of Electrical Engineering, Wuhan University, Wuhan 430072, China)

Electric vehicle (EV) has a promising future due to its friendliness to the environment and potential to reduce dependence on fossil fuels. If large-scale EVs access to the power grid charging disorderly, it may lead to some problems in power grid, such as power congestion. This will threaten the security and economic operation of power grid. Therefore, a EVs’ charging and discharging optimal scheduling strategy based on bi-layer optimization is proposed: in the transmission system, with the objective of reducing the operation costs and PM2.5 emissions of generators, charging cost of users and wind curtailment of wind farms, the upper layer optimization model is built based on day-ahead unit commitment (UC); in the distribution system, with the goal of reducing the network loss, the lower layer optimization model is built based on OPF considering network constraints and mobility of EVs. Based on a power system model consisting of a 10-unit transmission grid and an IEEE 33-bus distribution grid, the effectiveness and superiority of proposed bi-layer optimization strategy is investigated. This work is supported by National Natural Science Foundation of China (No. 51277135) and Science and Technology Project of Hebei Electric Power Company and Central University Science Foundation (No. 2042015kf1004).

electric vehicle; bi-layer optimization of charging and discharging strategy; unit commitment; OPF

2015-09-18；

2016-01-18

胡文平(1968-)，男，高级工程师，研究方向为电力系统规划；E-mail: hwp8@163.com

(编辑 葛艳娜)

10.7667/PSPC151672

国家自然科学基金项目(51277135)；河北省电力公司科技项目和中央高校基本科研业务费专项资金(2042015kf1004)资助

陈杰军(1994-)，男，通信作者，硕士研究生，研究方向为电力系统保护。E-mail: 2011302540279@whu.edu.cn