动力总成悬置系统对汽车动力学性能的影响*

宋 康,陈潇凯,林 逸

(1.北京理工大学机械与车辆学院,北京 100081； 2.北京汽车股份有限公司汽车工程研究院,北京 101300)

2016079

动力总成悬置系统对汽车动力学性能的影响*

宋 康1,陈潇凯1,林 逸2

(1.北京理工大学机械与车辆学院,北京 100081； 2.北京汽车股份有限公司汽车工程研究院,北京 101300)

在1/4车辆模型的基础上加入动力总成悬置系统而建立了汽车前轴垂向振动模型，基于该模型分析不同悬置系统设计对系统固有属性和汽车行驶动力学性能的影响。将线性2自由度汽车模型与动力总成悬置系统相结合，建立3自由度汽车侧向动力学模型，应用该模型计算整车在转向角阶跃输入和角脉冲输入下的响应，以分析不同悬置系统设计对汽车转向稳态与瞬态特性的影响。结果显示，动力总成悬置系统对车身加速度的影响很大，但对悬架动挠度和车轮动载荷影响很小；随着悬置系统侧向偏频的升高，汽车的横摆谐振频率增高，谐振峰值增大，而相位滞后角的变化很小。

动力总成悬置系统；垂向动力学；侧向动力学；固有属性；瞬态响应

前言

动力总成悬置系统是影响汽车NVH性能的关键子系统，其作用包括隔离动力总成的振动向车身传递，控制外部激励引起的系统振动和冲击等。

目前，动力总成悬置系统的设计方法已经趋于完善，最常用的有扭矩轴解耦法和弹性轴解耦法[1]。但这类方法在应用中通常假设动力总成安装于固定的刚性基础之上，从而忽略了汽车悬架和车身(或车架)等系统弹性的作用。针对该问题，文献[2]中应用4端参数技术分析弹性基础上发动机悬置的隔振性能，揭示了发动机悬置振动传递率曲线在高频下上扬的原因。文献[3]和文献[4]中采用有限元分析和试验测试得到的模态信息来表征底盘的弹性，动态响应结果显示，车架弹性对怠速振动和作用力传递有着重要影响。文献[5]中研究了悬置系统在整车环境下的分析和优化问题。文献[6]中扩展了扭矩轴解耦理论，使之适用于悬置系统安装在弹性基础上的解耦设计。上述文献主要讨论了外部弹性因素对动力总成悬置系统的影响，最终的研究对象和所得结论仍局限于悬置系统本身。但是，动力总成是除车身以外的最大集中质量体，如果不对其进行合理约束，就有可能造成车身的振动加剧等问题[7]。对此，文献[8]中提出可通过合理配置悬置系统的侧倾频率和跳动频率来降低车身和转向盘等处的振动水平。除了将动力总成作为吸振器，文献[9]中还指出车辆的行驶和操纵性能也受到悬置系统调校的影响。虽然现有文献已经对悬置系统与汽车动力学性能的关系有所涉及，但是并未对此问题展开进一步的分析，而所得出的少数结论也仅停留在定性分析阶段。

本文中针对动力总成悬置系统对汽车动力学性能的影响，分别建立了汽车前轴垂向振动模型和3自由度汽车侧向动力学模型，并基于所建模型分别分析了悬置系统对汽车垂向和侧向动力学性能的影响。

1 动力总成悬置系统对汽车垂向动力学性能的影响

解耦设计是动力总成悬置系统设计的重要内容，经过解耦的系统具有各向独立的振动，能为系统的分析与设计带来便利。假设动力总成悬置系统在垂向的振动完全解耦，并且动力总成的质心近似位于前轴上方，那么将悬置系统和1/4车辆模型相结合建立的汽车前轴振动模型如图1所示。

模型中，mp为动力总成的质量，200kg；km和cm分别为悬置系统垂向刚度和阻尼；mb为车身质量，767.31kg；ks和cs分别为悬架的刚度和阻尼；mu为非簧载质量，42.81kg；kt为轮胎垂向刚度，254N/mm；q为地面位移输入；F为动力总成的不平衡惯性力；zp，zb和zu分别为动力总成、车身和非簧载质量的位移，m。对比1/4车辆模型，该模型中的簧载部分由动力总成和车身两部分构成。

建立系统的运动方程：

(1)

其中：

广义坐标向量z=(zpzbzu)T

质量矩阵m=diag(mpmbmu)

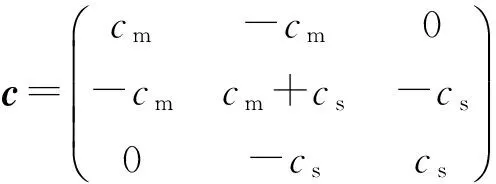
激励向量Q=(Fq)T。

1.1 悬置系统对系统固有属性的影响

确定动力总成悬置系统固有频率的分布范围的原则是根据发动机的怠速转速、结构类型和隔振设计要求确定系统频率的上限；根据整车其他子系统的频率配置确定系统频率的下限。以怠速转速600r/min为例，4缸、6缸和8缸发动机的怠速激振频率分别为20，30和40Hz，因此，按照有效隔振设计要求确定的系统频率分布上限分别为14.14，21.21和28.28Hz。根据不同车型整车各子系统的频率配置，一般将悬置系统的频率下限确定为5～6Hz。

在分析或设计动力总成悬置系统的固有属性时，一般将系统以下的安装固定部分简化为无运动的刚体(相当于直接固定在大地上)。虽然系统整体频率分布的可行范围已确定，但具体到系统的每阶频率却须要根据隔振、承重等设计要求制定详细的分布区间。以垂向振动频率为例，如果不考虑悬置系统具体结构的限制，那么该阶频率在理论上可配置为由第1阶频率至第6阶频率中的任一阶。因此，该阶频率的理论分布区间即为系统频率分布的可行范围。

借用1/4车辆模型中偏频的概念，将刚性固定基础假设下的悬置系统频率称为偏频，以区别于根据图1振动模型计算得到的悬置系统固有频率(弹性安装基础)。在小阻尼条件下，系统无阻尼固有频率和阻尼固有频率相差不大。因此，忽略阻尼的影响，悬置系统的垂向偏频ωp定义为

(2)

假定动力总成的质量mp不变，则悬置系统的偏频ωp与悬置刚度km有简单的一一对应关系。

为观察弹性基础对系统各阶固有频率，尤其是悬置系统垂向固有频率的影响，将簧载质量的偏频引入振动模型。对于该模型，忽略悬架阻尼的影响，簧载质量的偏频ωs定义为

(3)

同样，假定动力总成的质量mp和车身的质量mp不变，簧载质量的偏频ωs与悬架刚度ks也有简单的一一对应关系。

根据上述分析，假定悬置系统垂向偏频的理论分布范围是[5，30]Hz，同时选择簧载质量偏频的水平分别为0.8，0.9，1.0，1.1和1.2Hz。忽略系统中所有阻尼的影响，在每个水平的簧载质量偏频下，分析悬置偏频的变化对振动系统各阶固有频率的影响。结果分别如图2～图4所示。

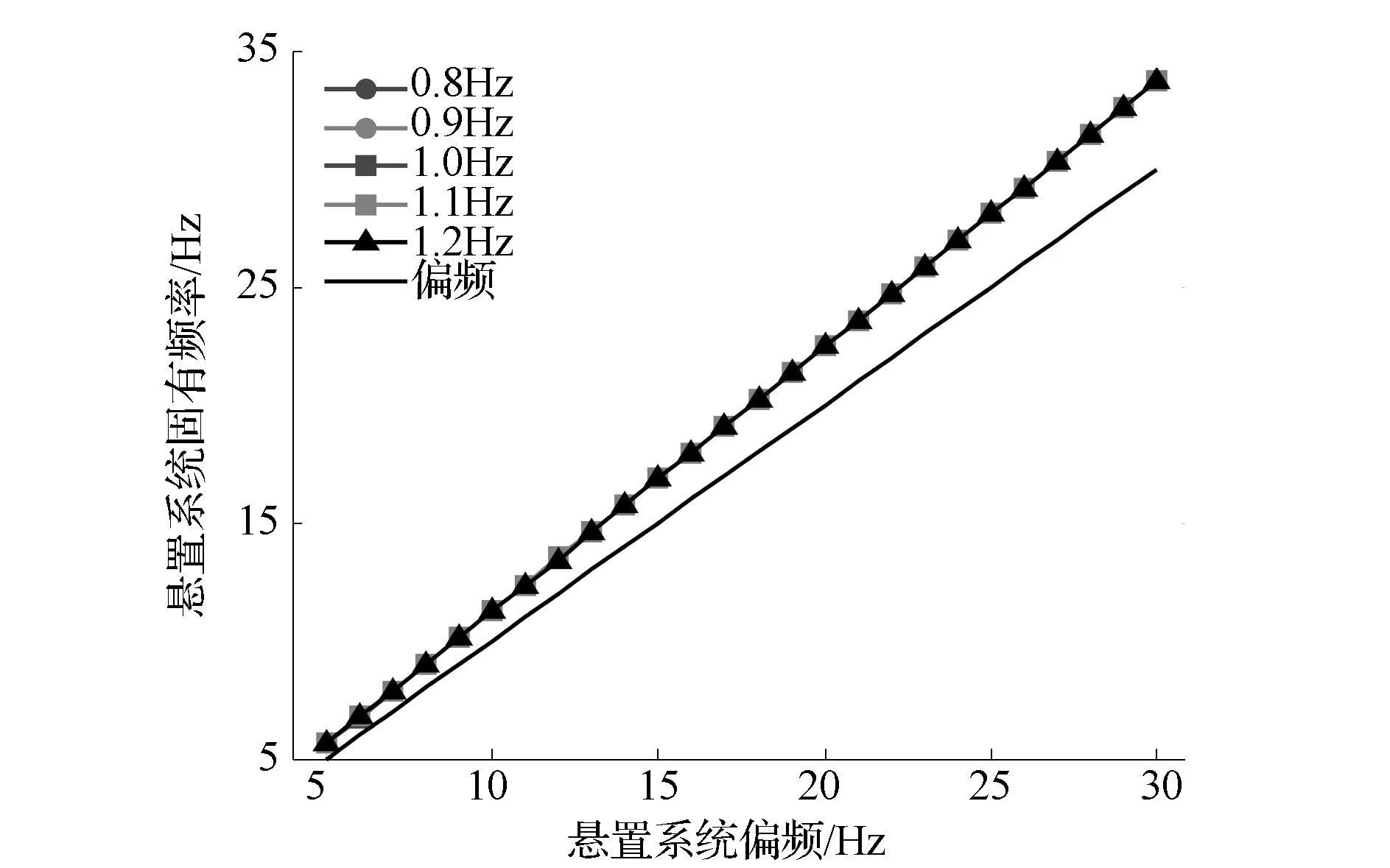
图2 悬置偏频对悬置系统固有频率的影响

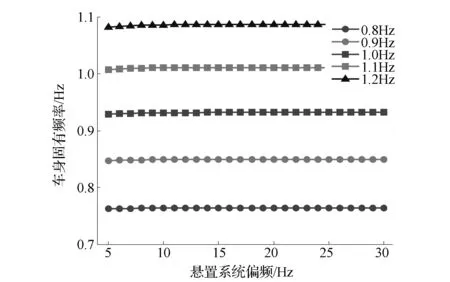
图3 悬置偏频对车身固有频率的影响

图4 悬置偏频对非簧载质量固有频率的影响

由图2可见，在悬置系统偏频的整个变化范围内，计算得到的悬置系统固有频率(第2阶频率)均大于对应的偏频值；同时，簧载质量偏频的变化对悬置系统的固有频率几乎没有影响。这说明，在计算悬置系统的固有频率时，刚性固定基础的假设并不准确，悬置系统以下的弹性安装基础对系统的固有频率有着一定的影响，但该影响对簧载质量偏频或悬架刚度的变化不敏感。

在簧载质量偏频等于0.8Hz的条件下，悬置系统偏频取5,10和15Hz时的系统第2阶模态向量分别为[0.96，-0.25，-0.09]，[0.96，-0.25，-0.09]和[0.97，-0.25，0.03]。这说明，在系统发生第2阶固有振动时，动力总成与车身反向运动，因而导致悬置系统的固有频率大于偏频值。另外，随着偏频的增高，悬置系统的刚度值不断增大，而动力总成与车身在固有振动中的幅值比却基本保持不变，这将使悬置系统的固有频率与偏频之差逐渐增大。计算结果显示，该差值在偏频取5，10和15Hz时分别为0.63，1.23和1.85Hz。

由图3可见，对于所有水平的簧载质量偏频，悬置系统偏频的变化对车身固有频率(第1阶频率)几乎没有影响。当悬置系统偏频等于5Hz的条件下，簧载质量偏频取0.8，0.9和1.0Hz时的系统第1阶模态向量分别为[0.71，0.70，0.06]，[0.72，0.69，0.08]和[0.72，0.69，0.09]。这表明，在系统发生第1阶固有振动时，动力总成与车身几乎同向、同幅值振动，因此可将二者看作一个刚体；同时，由于非簧载质量与车身也是同向振动，故车身部分的固有频率要小于簧载质量的偏频。

由图4可见，在簧载质量偏频的整个变化范围内，除13Hz外，悬置系统偏频的变化对非簧载质量的固有频率(第3阶频率)几乎没有影响。这说明，对于所有水平的簧载质量偏频，非簧载质量的偏频大约为13Hz。因此，当悬置系统的偏频位于13Hz附近时，动力总成和非簧载质量在系统发生第3阶固有振动时有较强的耦合作用，从而引起非簧载质量的固有频率发生较大的波动。所以，动力总成悬置系统的垂向频率应避开非簧载质量的频率，以避免二者之间较强的耦合。

1.2 悬置系统对垂向动力学性能的影响

对于1/4车辆模型，垂向动力学性能的评价指标通常是车身加速度、悬架动挠度和车轮动载荷。车身加速度直接反映了乘坐舒适性的优劣；悬架动挠度关系到悬架限位块起作用的频率，从而间接影响乘坐舒适性；车轮动载荷表征了轮胎接地力的变化情况，与汽车操纵稳定性关系密切。

在本文中，由于模型中引入了动力总成悬置系统，故车身加速度的含义与1/4车辆模型不同。新模型可直接采用车身的加速度，而1/4车辆模型的车身加速度实质上是簧载质量的加速度。悬架动挠度与车轮动载荷的定义与1/4车辆模型相同。

假定动力总成悬置系统垂向偏频的理论分布范围是[5，30]Hz，阻尼比的理论分布范围是[0.01，0.3]。在车速为90km/h，C级路面输入的条件下,分析二者的变化对汽车垂向动力学性能的影响，结果分别如图5～图7所示。

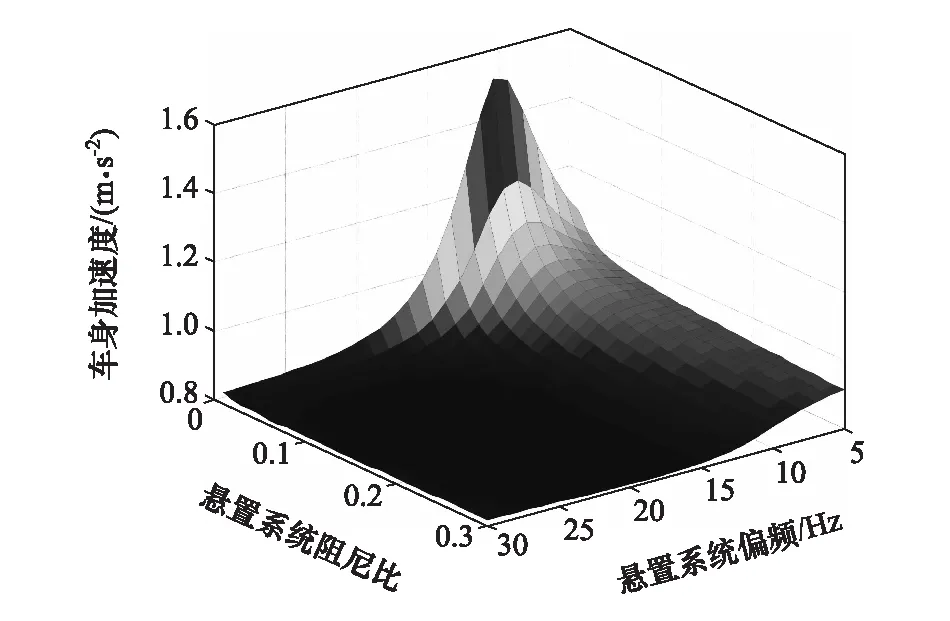
图5 悬置系统的偏频和阻尼比对车身加速度的影响

图6 悬置系统的偏频和阻尼比对悬架动挠度的影响

图7 悬置系统的偏频和阻尼比对车轮动载荷的影响

假设汽车垂向动力学性能的第i个评价指标为PIi，则该指标的均方值为

(4)

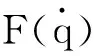
由式(4)可知，性能指标PIi的均方值与Gq(n0)和u的乘积成正比，因此，当Gq(n0)和/或u增大时，均方值的计算结果都是在原始结果的基础上乘以某个系数而得到的。由于Gq(n0)和u表征了汽车的行驶工况，因此可知行驶工况的变化不会对分析结果产生影响，系统分析可在任意工况下进行。

由图5可知，当阻尼比较低时，随着悬置系统偏频的增高，车身加速度呈现先增大后减小的趋势，最大值大约出现在偏频13Hz处。根据第1.1节中的分析可知，当悬置系统的偏频取13Hz时，动力总成的运动与非簧载质量的运动有着较强的耦合。因而，当悬置系统的偏频接近非簧载质量的频率时，汽车的乘坐舒适性和动力总成在垂向的运动控制都将受到不利影响。当阻尼比较高时，随着悬置系统偏频的增高，车身加速度呈现平滑下降的趋势。当偏频高于15Hz后，车身加速度处于较低的水平，变化趋势不再明显。对于任意的悬置系统偏频，随着阻尼比的增大，车身加速度呈现平滑下降的趋势。但当偏频取值较小时，下降趋势较为明显；而当偏频取值较大时，下降趋势则不很明显。

由图6可知，当悬置系统的偏频取值较小而阻尼较大时，悬架动挠度达到最小值；当偏频取值大于15Hz后，悬架动挠度基本不再发生变化。但在悬置系统偏频和阻尼比的整个变化范围内，悬架动挠度很小，最大值与最小值之差仅为0.03mm。因此，悬置系统对悬架动挠度的影响较小。

由图7可知，悬置系统对车轮动刚度的影响与车身动挠度基本相同。但是，与悬架动挠度相似，在悬置系统偏频和阻尼比的整个变化范围内，车轮动刚度的变化范围也很小，最大值与最小值之差仅为5.53N。因此，悬置系统对车轮动刚度的影响也较小。

2 动力总成悬置系统对汽车侧向动力学性能的影响

假设动力总成悬置系统在纵向和侧向的振动完全解耦，且动力总成的质心近似位于前轴上方，将线性2自由度汽车模型(自行车模型)与动力总成悬置系统相结合，建立汽车3自由度侧向动力学模型，如图8所示。

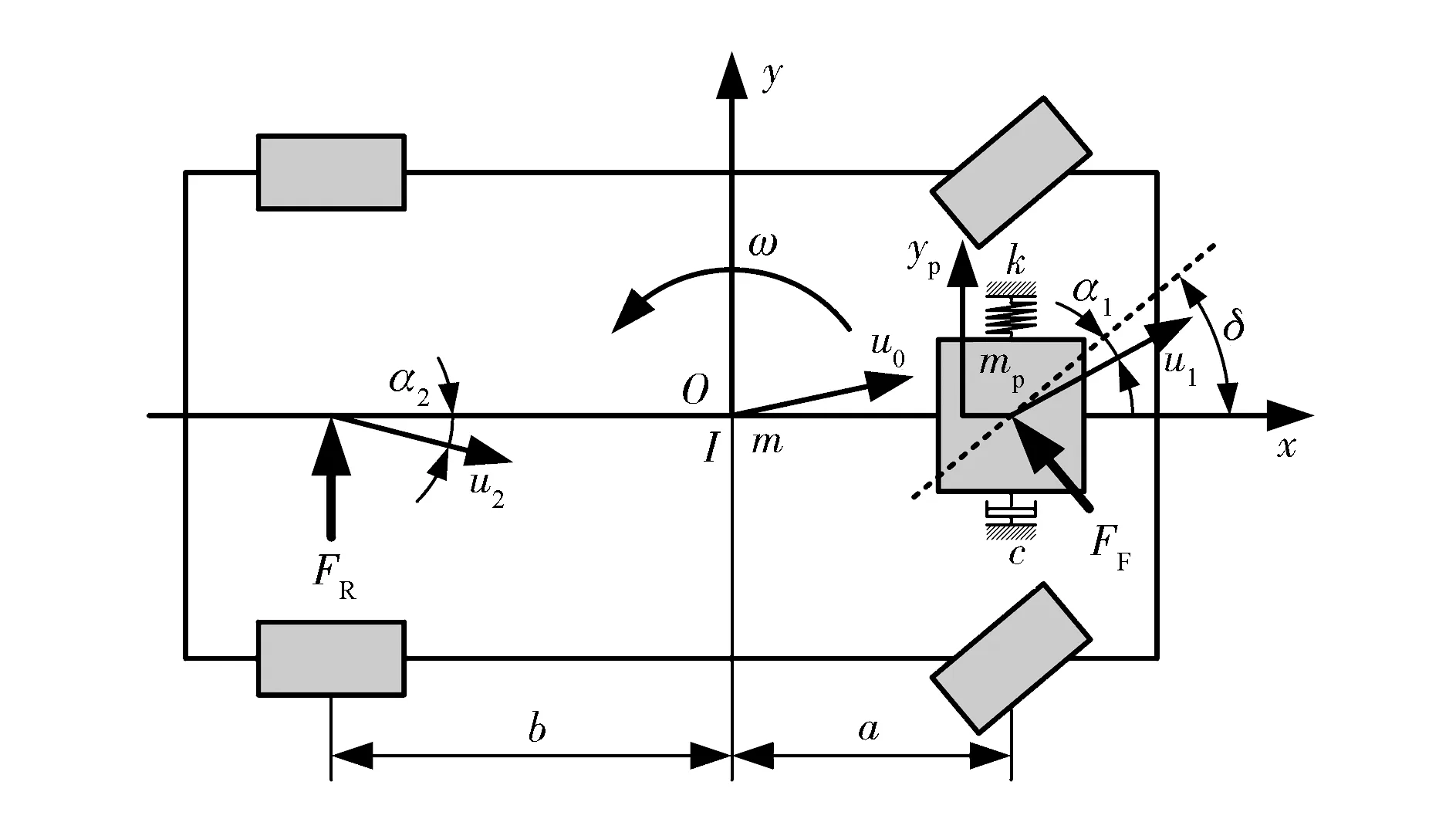
图8 汽车3自由度侧向动力学模型

图9 汽车各点速度关系

假设汽车沿x轴方向的速度保持恒定，则可忽略动力总成相对车身的纵向运动，而只考虑其侧向运动。汽车质心速度、前轴速度(动力总成)和后轴速度的关系如图9所示，三者在x轴方向的投影均为u。

建立汽车3自由度侧向动力学模型的运动方程：

(5)

式中:mp为动力总成的质量，kg；m和I分别为以车身为主体的汽车其他子系统的总质量和通过质心绕垂直轴的转动惯量，kg和kg·m2；k1和k2分别为前轴和后轴的侧偏刚度，N/rad；a,b和l分别为其他子系统的质心至前轴轴线、后轴轴线和动力总成质心沿x方向的距离，m；k和c分别为悬置系统在侧向的刚度和阻尼；u和v分别为汽车在x轴、y轴方向的速度分量，m/s；ω为汽车横摆角速度，rad/s；yp为动力总成相对车身的侧向位移，m。

在2自由度模型中，假设整车的质量为M，绕z轴的转动惯量为I0。当模型中引入动力总成悬置系统后，整车可分为两部分：一部分是动力总成；另一部分是以车身为主体的汽车其他子系统。根据直接测得的整车与动力总成的质量和转动惯量，计算3自由度模型中车身的质量、转动惯量和质心位置。

具体步骤如下所述。

(1)质量相等原则：

M=m+mp

(6)

(2)转动惯量相等原则(忽略动力总成绕通过其质心的z轴的转动惯量)：

I0=m(a-A)2+I+mp(l-a+A)2

(7)

式中A为整车质心至前轴沿x方向的距离(由于动力总成前置，故A要小于a)。

(3)前、后轴质量分配相等原则。以后轴质量为例：

(8)

式中L为轴距。

根据式(6)～式(8)计算得

式中λ为动力总成与整车的质量比，λ=mp/M。

模型中各参数的数值如表1所示。

表1 汽车3自由度侧向动力学模型参数值

2.1 角阶跃输入下的汽车瞬态与稳态响应分析

根据国家标准《GB/T 6323—2014汽车操纵稳定性试验方法》，在汽车前轮上施加角阶跃输入以进行瞬态响应试验。

试验车速按照汽车最高车速的70%确定，为140km/h；阶跃输入的最终转角按照汽车稳态侧向加速度为4m/s2确定；在时间为1s时开始施加阶跃输入，施加过程历时0.3s。

汽车横摆角速度的时域响应曲线如图10所示，图中对比了悬置系统的侧向偏频为5和20Hz及原始2自由度模型的横摆角速度响应曲线。

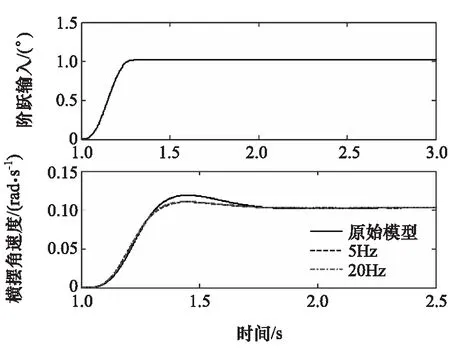
图10 转向阶跃输入下的横摆角速度响应

由图10可见，悬置系统偏频为5和20Hz时的横摆角速度响应曲线相差不大，但二者与2自由度模型的响应曲线却有明显的差别。说明悬置系统偏频在可行范围内的变化对汽车横摆角速度响应的影响很小；但是，悬置系统的引入却对汽车横摆角速度响应有着较为明显的影响，2自由度模型横摆角速度响应的最大值大于3自由度模型。因此，为能更精确地预测汽车对转向输入的响应，必须考虑动力总成悬置系统的影响。

汽车在转向角阶跃输入下的稳态响应是等速圆周运动。由图10还可见，各曲线在2s以后均趋于稳定，且最终的稳态值也相同。稳态横摆角速度增益与车速、整车质量、质心位置和轮胎侧偏刚度有关，而2自由度模型与3自由度模型在这些方面均相同，因此悬置系统的引入不会对汽车的稳态特性产生影响。

根据横摆角速度的响应曲线计算响应时间、峰值响应时间和超调量(各指标定义参考测试标准)，结果如图11所示。由图11中可见，悬置系统偏频的变化对响应时间和峰值响应时间都没有产生明显的影响。由于记录时间的最小分辨率为0.001s，故响应时间和峰值响应时间的变化曲线没有呈现出比较直观的变化趋势。超调量的曲线显示，在悬置系统的偏频由6Hz增高的过程中，超调量呈现缓慢增大的趋势，但是15Hz以后超调量趋于稳定。当悬置系统的偏频由5Hz增大至6Hz时，超调量有所下降。出现该现象的原因是当悬置系统的偏频较低时，动力总成会产生相对车身的幅值较大的振动，该振动与车身响应有着较强的耦合，使横摆角速度响应曲线出现微小的“高频”(相对汽车横摆固有频率而言)波动，增大了响应的最大值，从而造成超调量增大。

图11 转向阶跃输入下的各项性能指标

对于原始的2自由度模型，根据横摆角速度响应计算得到的响应时间、峰值响应时间和超调量分别为0.14s，0.301s和15.90%。前两者相对3自由度模型变化不大，而超调量相对3自由度模型却明显增大。

2.2 角脉冲输入下的汽车瞬态响应分析

根据国家标准《GB/T 6323—2014汽车操纵稳定性试验方法》，在汽车前轮上施加角脉冲输入以进行瞬态响应试验。

试验车速按照汽车最高车速的70%确定为140km/h；脉冲输入的最大转角按照汽车侧向加速度的最大值确定为4m/s2；在时间为1s时开始施加阶跃输入，施加过程历时0.3s。

对汽车的转向输入和横摆角速度响应分别进行傅立叶变换，然后根据二者的比值计算得到横摆角速度的频率响应特性。汽车横摆角速度的频率响应曲线如图12所示，图中给出了悬置系统偏频为5和20Hz时及原始2自由度模型的横摆角速度频率响应曲线。根据横摆角速度的频率响应曲线计算谐振频率、谐振峰值和相位滞后角(各指标定义参考标准《QC/T 480—1999汽车操纵稳定性指标限值与评价方法》)，结果如图13所示。

图12 汽车横摆角速度频率响应曲线

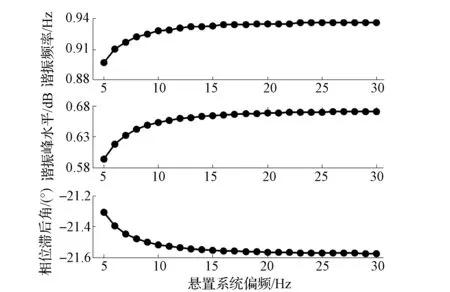
图13 转向脉冲输入下的各项性能指标

由图12可知，当悬置系统的偏频由5升至20Hz时，横摆角速度的频响曲线变化不大，但是二者与2自由度模型的计算结果有着明显的差别。当转向输入频率较低时，2自由度模型和3自由度模型的横摆角速度增益相差不大；当转向输入频率接近系统的谐振频率时，两个模型横摆角速度增益的差别最大。至于相位滞后角，当频率小于0.8Hz时，2自由度模型的滞后角(本文中如不作特殊说明，均指绝对值)略小于3自由度模型；而当激励频率大于0.8Hz时，2自由度模型的滞后角大于3自由度模型，且二者之差随着频率的增大而加大，说明2自由度模型对低频转向输入的响应更快，而3自由度模型对高频转向输入的响应更快。

由图13可见，随着悬置系统偏频的升高，谐振频率、谐振峰值和相位滞后角均呈现逐渐增大的趋势。但当偏频大于15Hz后，增大的势头趋于平缓。横摆角速度响应的谐振频率一般要求越大越好，因此设计中应将悬置系统的侧向频率配置得高一些；但是，随着偏频的升高，谐振峰值也逐渐增大，这与该指标的理想设计要求相悖；虽然相位滞后角随偏频呈现增大趋势，但变化很小。

对于原始的2自由度模型，根据横摆角速度频率响应曲线计算得到的谐振频率、谐振峰值和相位滞后角分别为1.04Hz，1.74dB和-23.65°。相对3自由度模型，3项指标均出现了明显的变化。

3 结论

(1)在悬置系统垂向偏频的合理变化范围内，悬置系统的固有频率均大于对应的偏频值，车身和非簧载质量的固有频率几乎不发生变化；在簧载质量偏频的合理变化范围内，悬置系统的固有频率几乎不变化。

(2)当悬置系统的垂向阻尼较低时，车身加速度随系统垂向偏频的升高呈现出先增大后减小的变化趋势；当悬置系统的垂向阻尼较高时，车身加速度随系统垂向偏频的升高呈现出平稳减小的变化趋势；当悬置系统的频率接近非簧载质量的频率且系统垂向阻尼较小时，车身加速度最大；悬置系统的垂向偏频和阻尼对悬架动挠度和车轮动载荷的影响很小。

(3)为了更加准确地预测汽车对转向输入的响应，有必要考虑动力总成悬置系统的影响。

(4)对于汽车在转向角阶跃输入下的横摆角速度响应，悬置系统侧向偏频的变化对响应时间、峰值响应时间和超调量的影响不大；但当悬置系统的侧向偏频较低时，动力总成的侧向运动与车身的横摆运动会产生较强的耦合进而引起横摆角速度的超调量增大。

(5)随着悬置系统侧向偏频的升高，整车的横摆谐振频率有增高的趋势，但同时会伴随谐振峰值的增大；相位滞后角虽有增大的趋势，但变化很小。

[1] JEONG T, SINGH R. Analytical Methods of Decoupling the Automotive Engine Torque Roll Axis[J]. Journal of Sound and Vibration, 2000, 234(1):85-114.

[2] 史文库，林逸，张建文，等．考虑弹性基础的发动机悬置隔振特性分析[J]．内燃机学报，1998，16(2)，232-237.

[3] KIM J, JHO S, YIM H.Influence of Chassis Flexibility on Dynamic Behavior of Engine Mount Systems[C]． SAE Paper 942269.

[4] KIM J H, LEE J M. Elastic Foundation Effects on the Dynamic Response of Engine Mount Systems[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2000, 214(D1): 45-53.

[5] 王峰，靳永军，张建武．基于整车模型的动力总成悬置振动仿真及优化[J]．振动与冲击，2008，27(4)：134-138.

[6] HU J F, SINGH R.Improved Torque Roll Axis Decoupling Axiom for a Powertrain Mounting System in the Presence of a Compliant Base[J].Journal of Sound and Vibration,2012,331(7):1498-1518.

[7] Timpner F F.Design Consideration in Engine Mounting[C]. SAE Paper 650093.

[8] GECK P E, PATTON R D.Front Wheel Drive Engine Mount Optimization[C]. SAE Paper 840736.

[9] AKANDA A, ADULLA C. Application of Evolutionary Computation in Automotive Powertrain Mount Tuning[J]. Shock and Vibration, 2006, 13(2): 85-102.

Effect of Powertrain Mounting System on Dynamics Performances of Vehicle

Song Kang1, Chen Xiaokai1& Lin Yi2

1.SchoolofMechanicalEngineering,BeijingInstituteofTechnology,Beijing100081;2.BeijingAutomotiveTechnologyCenter,BAICMotorCorporationLtd.,Beijing101300

Powertrain mounting system (PMS) is added on a 1/4 vehicle model to form a vertical vibration model for vehicle front axle, based on which the effects of different designs of PMS on the natural properties of system and the driving dynamic performance of vehicle are analyzed. Meanwhile, a 2 DOF linear vehicle model is combined with PMS to build a 3 DOF vehicle lateral dynamic model, with which the vehicle responses to both the step and pulse input of steering angle are calculated to analyze the effects of different designs of PMS on both the steady state and transient steering characteristics of vehicle. The results indicate that PMS has significant effects on vehicle body acceleration, but only has a trivial effect on the dynamic deflection of suspension and the dynamic load of wheel. With the increase in lateral partial frequency of PMS, yaw resonance frequency rises, resonance peak goes up but phase angle only has little change.

powertrain mounting system; vertical dynamics; lateral dynamics; natural properties; transient response

*国家自然科学基金(51275040)资助。

原稿收到日期为2015年1月16日。