基于效率优化的纯电动汽车双电源工作模式切换策略的研究*

陈 龙，周文竞，盘朝奉，陈 燎

(1.江苏大学汽车与交通工程学院，镇江 212013； 2.江苏大学汽车工程研究院，镇江 212013)

2016068

基于效率优化的纯电动汽车双电源工作模式切换策略的研究*

陈 龙1,2，周文竞1，盘朝奉1,2，陈 燎1

(1.江苏大学汽车与交通工程学院，镇江 212013； 2.江苏大学汽车工程研究院，镇江 212013)

为了提高双电源电动汽车动力系统效率，对电池、超级电容和电机等子模块进行了建模和工作过程的效率分析，以揭示在蓄电池单驱、蓄电池和超级电容双驱和预充电3种驱动模式下电动汽车动力系统效率随车速和加速度而变化的规律。基于效率最优的原则，在Matlab/simulink环境下研究了电动汽车动力系统的控制策略，使电动汽车能够合理切换工作模式，使动力系统工作在效率最优的区域，延长电动汽车的续驶里程。

双电源；控制策略；效率最优；超级电容

前言

纯电动汽车的污染小，噪声小，结构、控制和维护简单，逐渐成为新能源汽车中重点发展的车型[1]，使以电池、电机和整车控制技术为核心的动力驱动系统产生重大技术变革，动力驱动和整车控制成为重要的技术竞争领域。

近几年，诸多文献对纯电动车的控制策略进行了研究[2-3]。文献[2]中搭建了纯电动汽车动力总成系统仿真模型，利用建立的模型对纯电动汽车的起步加速过程进行优化。文献[3]中对蓄电池-超级电容的复合储能系统在4种能量管理策略下进行了经济性分析，发现基于规则的控制策略具有较低的运行成本。可见，提高纯电动车的效率是制定驱动策略的重要依据，基于规则的能量管理策略是实现效率优化的重要手段。

蓄电池的功率密度低，以蓄电池为单一电源的纯电动汽车，动力性和经济性受到极大限制。将超级电容引入电动汽车的储能系统中，利用其高功率密度的特点弥补蓄电池的不足[4-5]。超级电容功率密度大，能够配合电池的输出电流满足车辆大功率工况下转矩和功率的需求，保证电池的输出电流平稳，提高电池和动力系统的能量效率，延长电池的寿命[5]。

本文中通过建立电动汽车动力系统的效率模型，分析在蓄电池单驱、蓄电池与超级电容双驱和蓄电池给超级电容预充电3种驱动模式[5]下电动汽车动力系统效率的变化规律，以效率优化为目标，研究基于规则的能量管理控制策略，并分析其控制效果。

1 动力系统控制策略的设计

1.1 复合电源电动车动力系统

超级电容-蓄电池复合电源电动车动力系统结构如图1所示。能量管理控制器负责协调分配超级电容、蓄电池的输出功率并发出指令。电机控制器的功能是控制电机的能量转化，车辆驱动时，控制电机将电能转化为动能；车辆制动时，控制电机将动能转化为电能[5]。

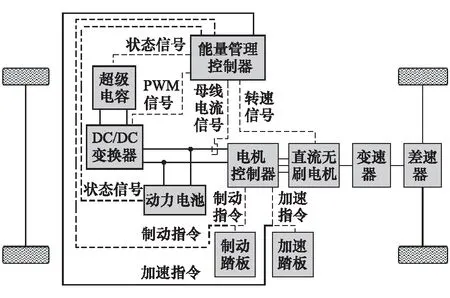
图1 复合电源电动车动力系统结构

1.2 电动汽车动力系统建模与效率分析

1.2.1 蓄电池模型及其效率特性分析

本文中采用的蓄电池基本参数见表1。

表1 蓄电池基本参数

常用的电池电路模型主要有线性模型、Thevenin模型和PNGV等效电路模型[4,6]。线性模型过于简单，误差较大；PNGV模型阶数高，参数难以确定。故本研究采用Thevenin模型[7-8]，如图2所示。图中E为开路电压，R1为极化电阻，C1为极化电容，R0为欧姆电阻，Ub为输出电压。

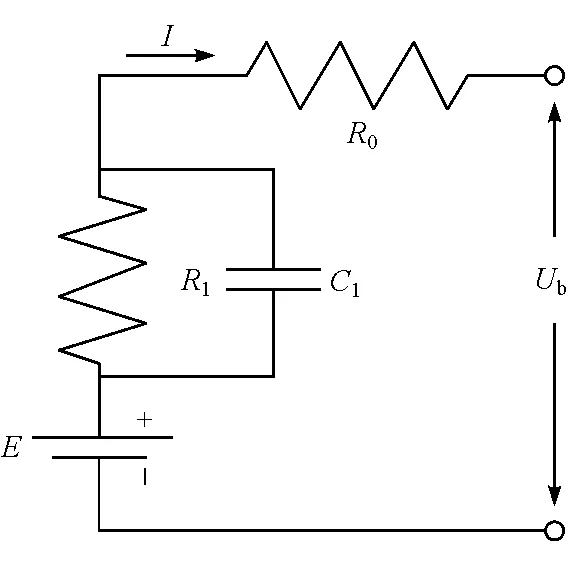
图2 蓄电池的等效电路模型

对锰酸锂电池的内阻特性进行测试与分析，可知欧姆电阻与极化内阻在放电时呈现的内阻特性为：荷电状态(state of charge, SOC)∈(0.2,0.9)时，电池内阻平稳；SOC∈[0,0.2]/[0.9,1]时，电池内阻较高[7]。在高电量低电量状态下电池的内阻较高，相同的放电电流导致较高的损耗；中间电量状态时，内阻较低且较为稳定，损耗较少。综上所述，本文中将电池分为两种工作状态：SOC∈[0,0.2]/[0.9,1]的低效率区和SOC∈(0.2,0.9)的高效率区。对蓄电池进行静置特性测试，获取该蓄电池在不同电池SOC下的欧姆电阻R0、极化内阻R1和极化电容C1[8]。将电池阻抗以表格形式输入电池的效率模型，根据SOC确定电池内部阻抗，理论计算出电池的损耗，其数学模型为

(1)

式中：U1为极化电压，即R1和C1两端电压；Pbw为功率损耗；I为输出电流。

1.2.2 超级电容模型及其效率特性分析

式(2)描述了超级电容的输出特性和能量特性，根据该式可确定超级电容的底线电压和最大放电电流为

(2)

式中：C为超级电容的电容值；Ut为额定电压；Ub为底线电压；η为逆变器的效率；Imax-sc为超级电容最大输出电流；Imax为超级电容输入到总线上的最大电流；Umax为总线上最大电压；Umin为超级电容最小输出电压；ΔE为超级电容可用的能量。采用软开关的DCDC逆变器在大输出功率下的效率高达95%[6,9-10],根据选用的软开关逆变器型号HWZ20的相关技术参数，设定其效率值η为0.95。选用电动车专用超级电容模组BMOD0165 P048。根据式(2)计算从额定电压开始放电至不同的底线电压所对应的超级电容可用能量、最大电流放电时间和最大允许电流，如表2所示。

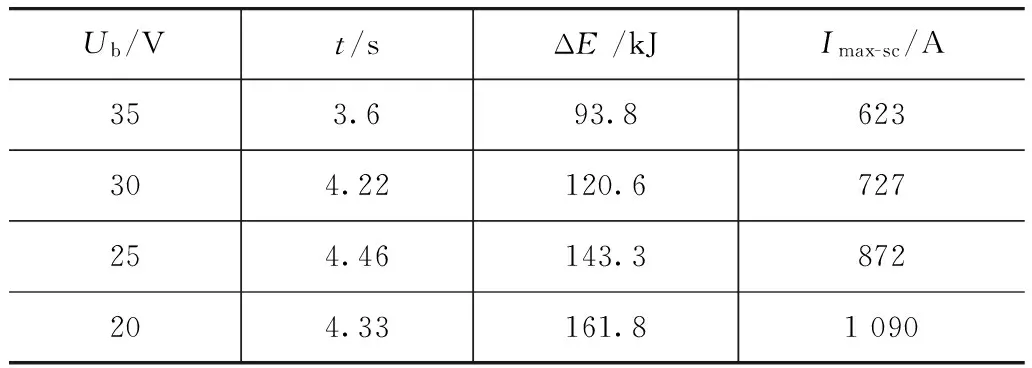
表2 超级电容底线电压对应表

结合表2中的值，设定Ub=25V。在该底线电压下，最大电流放电时间最长，放电深度达51.4%，可利用能量达143kJ。

目前超级电容的等效电路模型主要有经典拜德极化模型和Newman传输线模型[10-11]。上述两种模型虽精确度较高，但模型较复杂。在进行慢速和突加负载放电时，两种等效电路的放电电流和电容两端电压基本吻合[10,12]。本文中采用超级电容拜德极化模型的等效模型，如图3所示。图中C为超级电容的电容，Res为串联电阻，Rep为并联电阻。

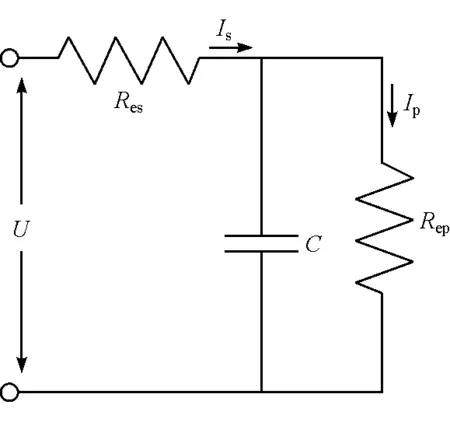
图3 超级电容等效电路模型

为合理利用超级电容的能量，本文中在额定电压Ut与底线电压Ub之间拟定两条电压线，UH和UL。超级电容端电压U在UH与Ut之间时，说明储存电量即将接近极限，优先采用双驱驱动；U在UL与Ub之间时，若SOC(0.2,1],电量充足，在无需超级电容供电的低需求功率下，优先采用预充电模式，若SOC(0,0.2]，电量低，则不考虑预充电模式；U在UH与UL之间时为效率区间，根据动力系统效率来区分单驱模式和双驱模式。本研究中设定UH=45V，UL=30V，如图4所示。超级电容分为3个工作状态：(1)端电压U(45,48.6]的优先双驱区；(2)端电压U(30,45]的效率区；(3)端电压U[25,30]的优先预充区。

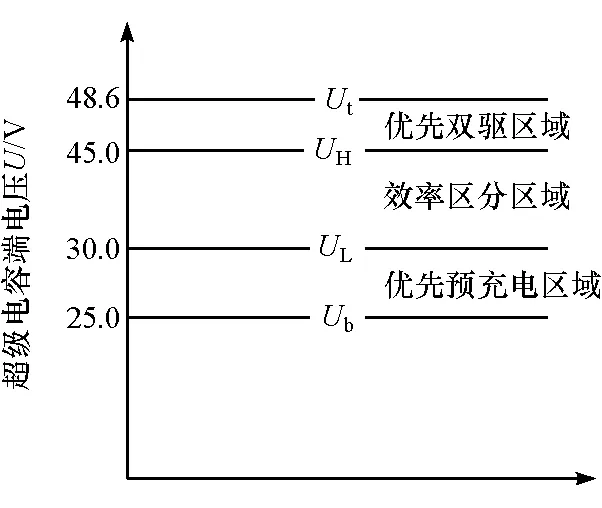
图4 超级电容工作状态划分

由于超级电容多工作在大电流状态，此时其内阻波动很小[13]，故在对超级电容建模时，只考虑定值串联电阻Res的损耗，而并联电阻上的漏电电流极小，可以忽略不计[13]，故超级电容损耗的数学模型为

(3)

式中：Pws为超级电容的功率损耗；Res为定值，可在超级电容的技术参数中获得。

1.2.3 电机效率特性分析

电机损耗的经验公式可参见文献[14]，但诸多损耗系数难以获得，直接用理论计算损耗有很大难度和误差。在生产厂商提供的电机效率MAP图谱的基础上，将关键点的电机效率运用表格的形式代入电机的效率模型，根据需求转速和转矩，运用分段线性插值的方法，直接得出电机瞬时效率ηe。

1.2.4 电动汽车动力系统效率模型构建和效率优化方法

采用逆向建模方法，即数据流方向和实际的能量流方向相反，以忽略驾驶员的影响，降低了模型复杂度，模型如图5所示。

根据蓄电池的效率分析，在模型中取SOC=0.6代表电池的高效率区进行仿真；取SOC=1代表低效率区仿真。超级电容端电压U[25,48.6]V，在模型中设定超级电容初始端电压U0=42V代表(35,48.6]的高工作电压区间，设定U0=30V代表[25,35]的低电压工作区间。以速度v和加速度a作为自变量计算系统效率。

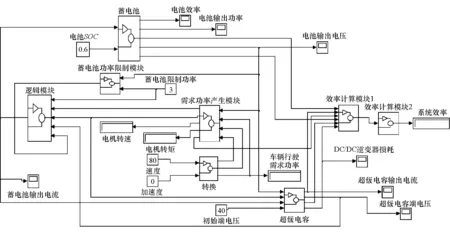
图5 效率优化算法模型

使系统效率最优的目标函数为

(4)

1.2.5 电动汽车的工作模式的区分

通过动力系统效率模型可计算各工况下蓄电池单驱模式和蓄电池-超级电容双驱模式的效率值，得出效率空间曲面图，并投影至v-a平面获得单双驱模式效率曲面的空间交线，如图6～图9所示，粗实线以上部分为双驱模式，粗实线及以下部分为单驱模式。

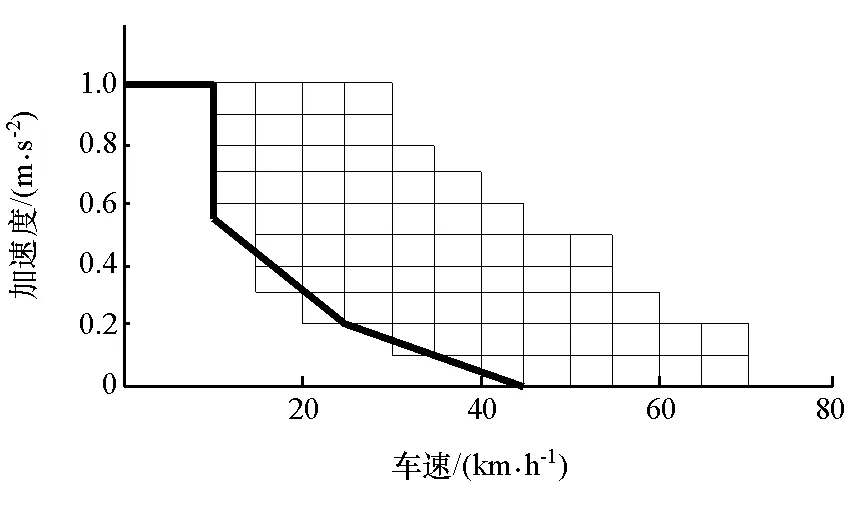
图6 工作模式区分1

(1) 电池处于高效率区间，超级电容处于高电压区间时，单双驱模式区分方法如图6所示。电池SOC(0.2,0.9)的高效率区，超级电容端电压U(35,48.6]的高工作电压区间,通过对数据的3次多项式拟合得到双驱模式的蓄电池优化输出功率为

PB1=[-0.3504,0.05726,2.936,-0.0002986,0.1945,-6.958,7.609e-6,-0.002048,0.07655,4.644]×[1,v,a,v2,va,a2,v3,v2a,va2,a3]T

式中：v为车速；a为加速度；PB1为输出功率，kW。

(2) 电池处于高效率区间，超级电容处于低电压区间时，单双驱模式区分方式如图7所示。电池SOC(0.2,0.9)的高效率区，超级电容外电压U(25,35]的低工作电压区间,通过对数据的3次多项式拟合得到，双驱模式的蓄电池优化输出功率为

PB2=[-0.4825,0.09645,1.26,-0.002179,-0.0983,1.373,3.008e-5,0.001303,0.1321,-4.031]×[1,v,a,v2,va,a2,v3,v2a,va2,a3]T

式中PB2为输出功率，kW。

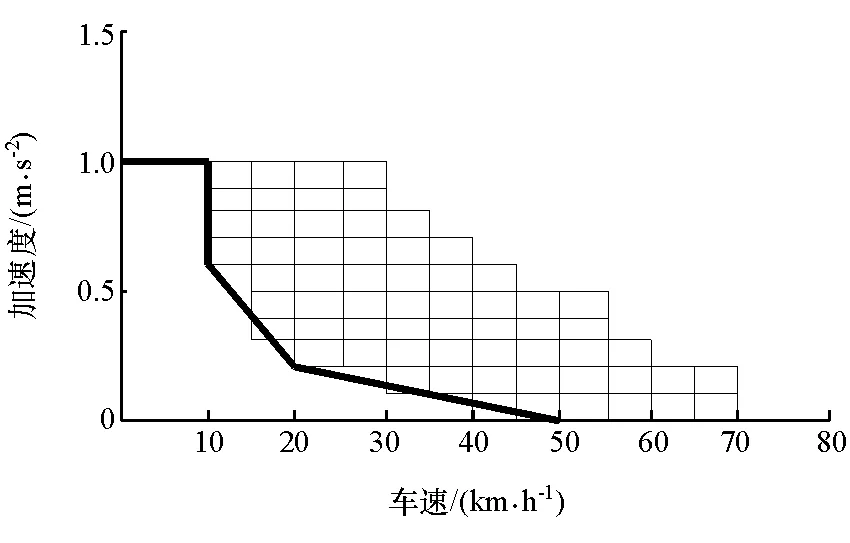
图7 工作模式区分2

(3) 电池处于低效率区间，超级电容处于高电压区间时，单双驱模式区分方式如图8所示。电池SOC(0,0.2]或[0.9,1]的低效率区，超级电容外电压U(35,48.6]的高电压区间,通过对数据的3次多项式拟合得到双驱模式的电池优化输出功率为

PB3=[-0.4587,0.1045,3.469,-0.002708,-0.1549,-3.421,2.504e-5,0.002379,0.1235,0.9143]×[1,v,a,v2,va,a2,v3,v2a,va2,a3]T

式中PB3为输出功率，kW。

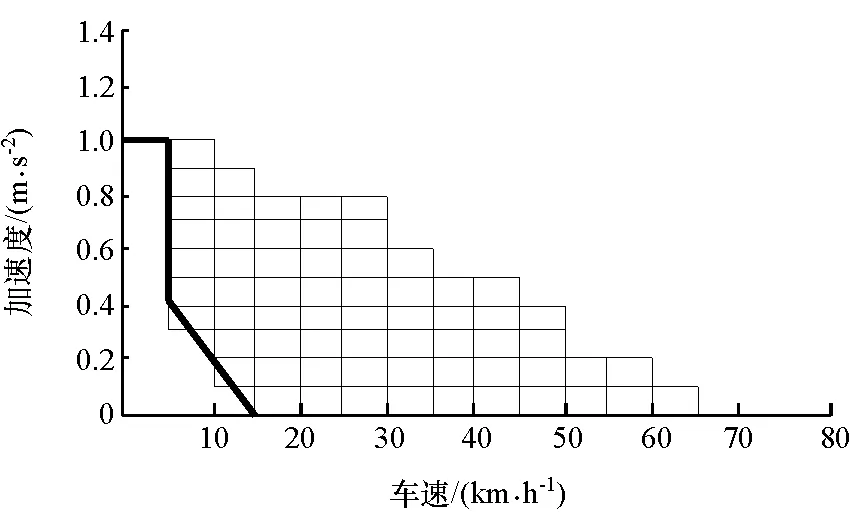
图8 工作模式区分3

(4) 电池处于低效率区间，超级电容处于低电压区间时，单双驱模式区分方法如图9所示。电池SOC(0,0.2]或[0.9,1]的低效率区，超级电容外电压U(25,35]的低工作电压区间,通过对数据的3次多项式拟合得到双驱模式的电池优化输出功率为

PB4=[0.2212,-0.01323,1.174,0.001982,-0.02571,-1.5,-2.5e-5,0.003214,0.2,0.4167]×[1,v,a,v2,va,a2,v3,v2a,va2,a3]T

式中PB4为输出功率，kW。

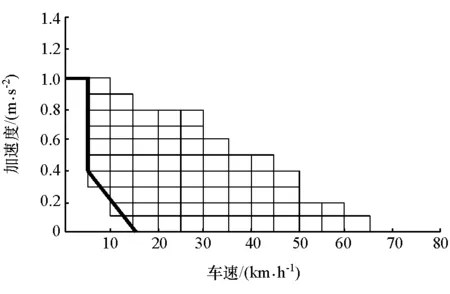
图9 工作模式区分4

1.3 整车驱动控制策略

整车驱动控制策略流程如图10所示。

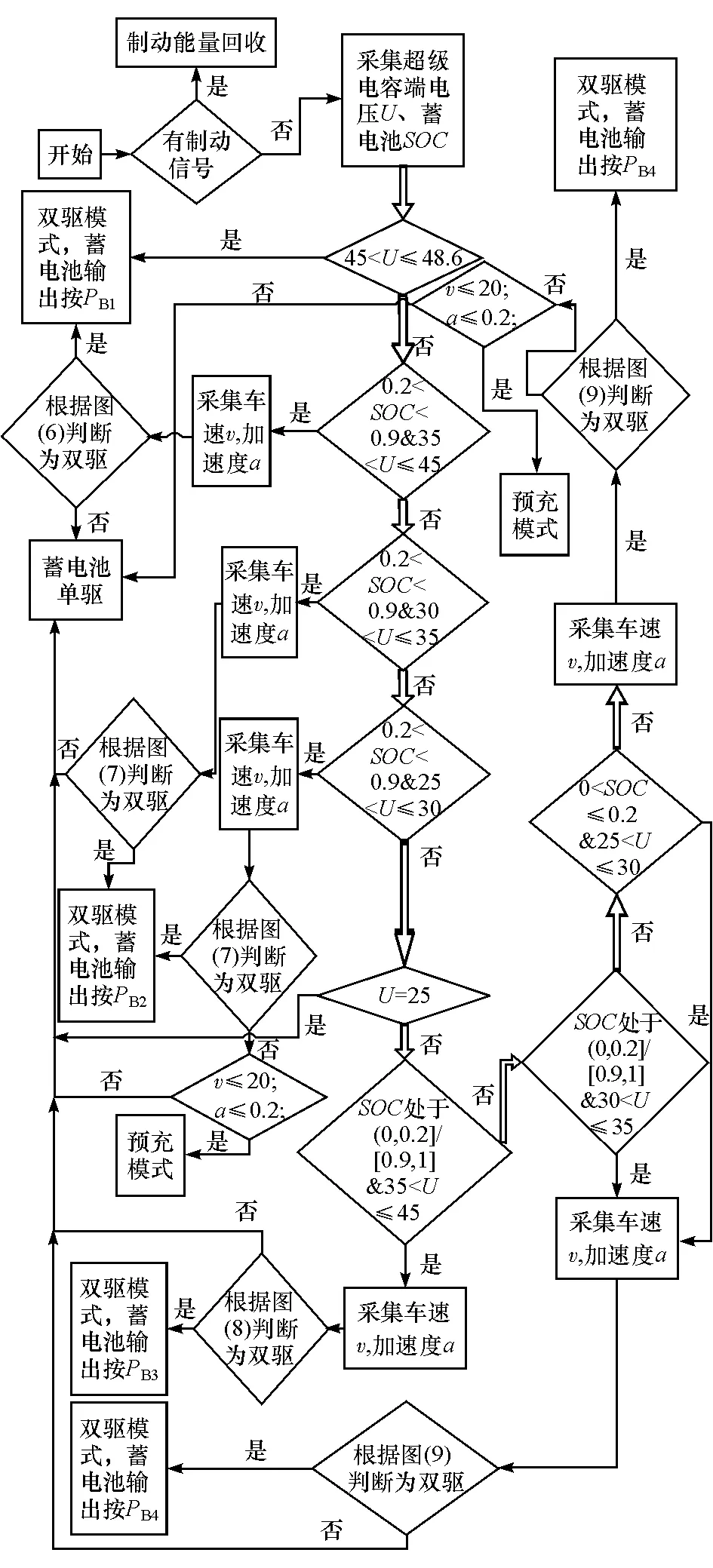
图10 驱动控制策略流程图

根据前面的分析可总结出基于效率最优的复合电源电动车的驱动控制策略：车辆在驱动过程中，传感器实时采集电动车的车速v、加速度a、蓄电池SOC和超级电容端电压U，首先根据SOC和U判断电池和超级电容所属的工作状态，再根据得到的工作状态、实时的车速和加速度判断系统进入单驱模式、双驱模式或是预充电模式，若进入单驱模式则停止超级电容的输出，使电池单独供电；若进入双驱模式则根据该工作状态对应的电池最佳输出功率调节蓄电池的输出功率；若进入预充电模式则选用对超级电容脉冲充电，最大限度地提高超级电容的能量接收率和能量效率[11]。

2 驱动控制策略的建模和仿真

2.1 驱动控制系统仿真模型的构建

为分析控制策略的控制效果，本文中建立了驱动控制系统的仿真模型，它包括蓄电池模型、超级电容模型、车辆行驶需求功率生成模型和逻辑分配模型(包括工作状态判断模块、电池输出功率限制模块和模式选择模块)4大部分。通过该模型可对控制策略的控制效果，电池和超级电容的工作状态进行仿真,仿真模型如图11所示。

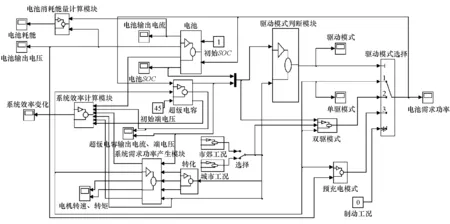
图11 控制策略仿真模型

2.2 驱动控制策略仿真分析

制动能量回收过程不在本文中的研究范畴，故在仿真时，设定制动能量回收率ζ=20%，回收率定义为

ζ=Er/En

(5)

En=ΔWn+Efn

(6)

式中：Er为能够回收到电容中的能量；En为制动区间能量变化；ΔWn为制动区间动能变化；Efn为制动区间阻力做功。驻车的行驶功率需求为零，近似认为系统效率为1。

2.2.1 循环工况下动力源的输出对比

采用《GB/T 18386—2005电动汽车能量消耗率和续驶里程实验方法》[15-16]中的基本市区循环工况，在电池SOC=0.8,超级电容端电压U=45V的初始条件下分析本控制策略下蓄电池的输出电流，结果如图12所示。可知，在瞬时大功率需求时，车辆进入双驱模式，蓄电池的输出电流相对稳定，且明显减小，输出功率按照前面制定的PB1输出。

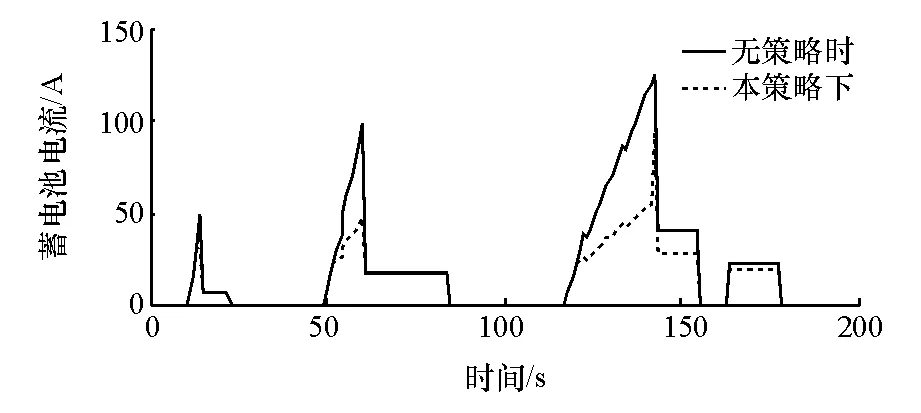
图12 循环工况下电动汽车蓄电池输出电流仿真结果

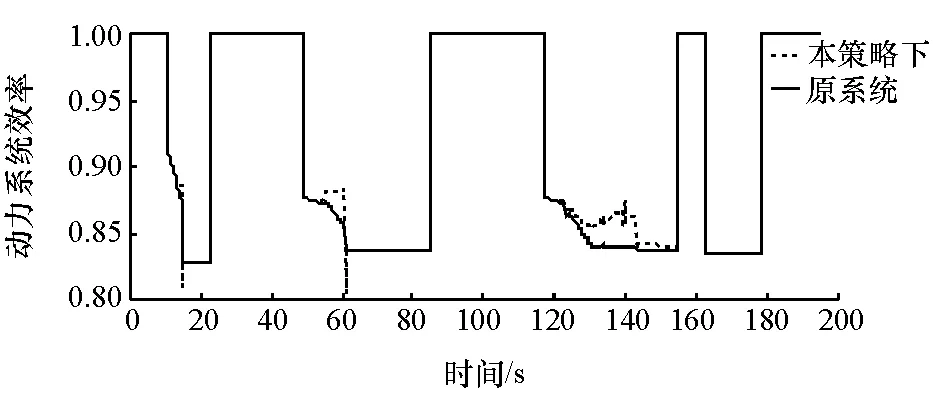
图13 基本市区循环工况下效率比较图

2.2.2 循环工况下整车经济性分析

在电池SOC=0.8，超级电容端电压U=45V的初始条件下，以基本市区循环工况为输入，仿真得到动力系统效率的变化情况，如图13所示(制动工况和驻车工况不在本文的考虑范畴，设其系统效率均为1)。在模式切换瞬间，超级电容停止大电流输出，使得系统电流出现跳动，系统瞬间效率降低，而其他情况下，本驱动策略有明显的效率优势。

根据图11，设定初始条件为超级电容电量充足，假设U=45V，以市区循环工况为输入，在不同电池SOC下运行仿真模型，可得到效率优化后的整车经济性。更改仿真模型，将动力源仅保留蓄电池，同样以市区循环工况为输入，可得优化前的整车经济性，优化前后能耗对比如表3所示。ΔE1和ΔE2分别表示优化前后整车能量损耗。

表3 整车能量损耗比较

以重复的基本城市循环工况为输入，从初始SOC=1开始，运行控制策略仿真模型，直至SOC=0.1，比较优化前后的车辆续驶里程，结果见表4。

表4 车辆续驶里程比较

由以上仿真结果可知，在本文中制定的策略下，单驱、双驱和预充电模式能够合理切换，并能够在车辆行驶需求功率较大的工况下使电动车进入双驱模式，减少蓄电池的负荷，同时降低系统的损耗，提高整车的能量效率和续驶里程。

3 结论

(1) 根据复合电源电动车的特点划分了电动车的驱动模式，并基于最优效率建立了系统效率模型和驱动模式识别和转换控制策略模型。

(2) 制定了纯电动车的驱动控制策略，划分了电池和超级电容的工作状态，在效率模型的基础上，结合效率优化算法，合理的区分了各种驱动工况。

(3) 仿真结果表明，所建立的模型和控制策略是可行的，能够有效提高系统的能量效率，延长续驶里程。

[1] LINDLY J K, HASKEW T A. Impact of Electric Vehicles on Electric Power Generation and Global Environmental Change[J]. Advances in Environmental Research,2002,6(6):291-302.

[2] 黄万有,程勇,纪少波,等.变工况下电动车驱动系统效率优化控制[J].电机与控制学报,2012,16(3):53-59.

[3] SONG I, HOLFMANN H, et al. Energy Management Strategies Comparison for Electric Vehicles with Hybrid Energy Storage System[J]. Applied Energy,2014,134:321-331.

[4] 左燕群,李仲兴,陈燎,等.电动汽车新型混合能源管理系统研究[J].电气传动,2011,41(10):21-24.

[5] 盘朝奉,何志刚,张德望,等.复合电源电动汽车动力系统建模与仿真[J].广西大学学报,2012,37(2):284-290.

[6] 沈乐析.三相无源软开关逆变器的损耗特性研究[D].沈阳:东北大学,2010.

[7] 叶贞.锂离子电池模型的建立及电池管理系统的研究[D].武汉:武汉理工大学,2013.

[8] 刘彦忠.车用动力电池充放电特性与智能管理技术[D].北京:北京交通大学,2012.

[9] 陈敏.BUCK型同步整流DC-DC转换器系统模型和效率研究[D].南京:东南大学,2005.

[10] 马奎安.超级电容储能系统中双向DC-DC变流器设计[D].杭州:浙江大学,2010.

[11] 汪亚霖,文方.超级电容充电策略研究[J].机械工程与自动化,2012(5):170-171.

[12] NELMS R M, CAHELA D R, NEWSSCOM R L. A Comparison of Two Equivalent Circuits for Double-layer Capacitors[C]. APEC,1999:692-698.

[13] 邓隆阳,黄海燕,卢兰光,等.超级电容性能试验与建模研究[J].车用发动机,2010(1):28-32.

[14] 陈小军.高速永磁无刷直流电机磁热耦合分析与效率优化研究[D].广州:广东工业大学,2013.

[15] 白中浩,曹立波.纯电动汽车用动力电池性能评价方法研究[J].湖南大学学报,2006,33(5):48-51.

[16] 全国汽车标准化技术委员会.GB/T 18386—2005电动汽车能量消耗量和续驶里程试验方法[S].北京:中国标准出版社,2005.

A Research on the Working Mode Switching Strategy for the DualPower of Electric Vehicle Based on Efficiency Optimization

Chen Long1,2, Zhou Wenjing1, Pan Chaofeng1,2& Chen Liao1

1.InstituteofAutomobileandTrafficEngineering,JiangsuUniversity,Zhenjiang212013;2.InstituteofResearchandAutomotiveEngineering,JiangsuUniversity,Zhenjiang212013

For enhancing the efficiency of dual power electric vehicles, the models for the sub-modules of battery, super capacitor and electric motor are set up, and the efficiency of system in working process is analyzed. The changing law of power system efficiency with the variations of vehicle speed and acceleration in three drive modes (battery drive alone, dual power drive and pre-charging) is revealed. Based on the principle of optimum efficiency, the control strategy for the power system of electric vehicle is studied under the environment of Matlab/ simulink to enable electric vehicle to reasonably switch its working modes and make power system operates in the region of optimum efficiency and extends the driving range of electric vehicle.

dual electric power; control strategy; optimum efficiency; super capacitor

*国家自然科学基金(51105178)、江苏省自然科学基金(BK2011489)、国家863计划项目(2012AA111401)、国家新能源汽车产业技术创新工程和江苏省“六大人才高峰”项目(2013-XNY-002)资助。

原稿收到日期为2014年11月24日，修改稿收到日期为2015年2月8日。