用“天下难事必作于易”指导数学教学

陈石生++吕志红

摘 要：在数学教学中，用老子的名言“天下难事必作于易”指导教学过程，从简单中找规律，解决小学六年级下册“数学思考”的问题。

关键词：教学思考；教学设想；教学过程

中图分类号：G623.5 文献标识码：A 文章编号：1009-010X（2015）32-0062-03

老子说：天下难事必作于易，天下大事必作于细。千年历史的浩瀚文海中有太多的名言警句吸引我们的目光，震撼我们的身心；但当我们被问题困扰不得其解的时候，细细地品味这句千年老话才发现，原来别有洞天，它对我们的工作有策略上的指导意义。这句古老的名言如何指导我们的教育教学呢？以人教版六年级数学下册第100页“数学思考”为例探讨。

一、教学设想

（一）分析课程标准要求

学生是教学活动的主体，教师应成为教学活动的组织者、指导者和参与者。教学过程中，教师要充分发挥创造性，依据学生的年龄特征和认知水平，设计探索性和开放性的问题，给学生提供探索的机会。让学生在观察、操作、讨论、交流、猜测、归纳、分析和整理过程中，理解数学问题的提出、数学概念的形成和数学结论的获得，以及数学知识的应用。通过这样的教学活动，逐步培养学生的创新意识，形成初步的探索和解决问题的能力。

（二）教学内容难度分析

对于本节课内容，如果按照常规的小组协作，则会不得要领；如果教师单纯讲授，学生可能依照教师归纳好的结论进行计算，类似问题也可能解决，但对学生而言，是机械地模仿，这是教学的下下策。因为学生没有经历思考，没有体验结论的产生，也就是没有实践课标要求的观察、操作、讨论、交流、猜测、归纳、分析和整理过程，问题的解决是没有基础的。空中楼阁怎样在教学过程中既符合课标的要求，又解决了问题？我经过反复的思考，从老子的“天下难事必作于易”受到启发，天下再难的事都是由简单的小事构成的，那么多的点，每个点之间相互连接成线段，确实使人数得头昏眼花，但是我们可以用推理去论证，可以从2点、 3点 、4点入手，从学生易懂易做的开始，由自己思考操作到同伴交流，使每一个学生都参与活动，都有机会表达自己的意见，并且使每一个学生都感到自己的存在价值，在不同的程度上得到提升。同时把老子的这句话也传授给学生，感受古老文化的博大精深。

（三）记录、观察、操作过程很关键

书写方式的不同，表示思维方式的区别，要细化过程，这对后期归纳规律至关重要。在老师的协助下，要体现再增加几条线段，而不是概括在一起有多少条线段。这一阶段是整个学习过程的关键，因为学生要有直观的感受，但是学生不能永远停留在直观上，他们要有高一级的思维、猜想、推理、验证，这才是教学的目标，是教学的精髓。怎样才能有猜想？要有教师的导学。教师要提出要求，第5个点和其他点的连线不要学生画出，提示学生可以根据以上的经验，猜想可能增加几条线段，说说为什么，然后大家做一做验证，6个点呢？这样就可以总结规律了。

随后就是代数式的运用。数学语言有文字语言、图形语言、符号语言。前两种语言在教学过程中通过学生的描述、画图得到了应用，符号语言就要在结论中以代数式的形式体现，多少个点用字母n表示，用含有字母n的式子得出有多少条线段的结论，本节课就基本完成了。数学知识方面就是这样的一个轮廓，怎样生动地引导学生进入问题情境中，是我最后考虑的问题。

数学来源于生活，指导生活，单单以点连线这个问题，无疑由点而连线。为做题而设计问题存在弊端，怎样才能把问题设计得有现实意义呢，我想到有类似之处的城市道路，它们的每个交叉点都有红绿灯，以改造升级城市街道红绿灯作为噱头，课题的导入就以一张简洁的城市交通地图开始。全城有多少条大道，每一条大道都互相交叉，在每个交叉点安装红绿灯，请学生计算最多需要多少组红绿灯。这样既有现实意义，又能激发学生的兴趣展开教学活动。

二、兴趣诱导（教学过程摘录）

教师：（播放一段自己拍摄的城市道路拥挤现场视频，展示一段摘录的城市夜景俯瞰图。）你看到了什么？想到了什么？

学生：看到城市拥挤的交通，四通八达的道路。想到疏导交通的交警和闪烁的红绿灯，……

教师：为了有效地疏导拥堵的人群，交管部门要升级改造交通信号灯，在市区的每个交叉路口设置红绿灯、电子眼。我们帮助交管部门计算一下最多要用多少组红绿灯，我们能做到吗？

学生：难，路口太多，太乱了。

教师：（出示老子语：天下难事必作于易，天下大事必作于细。并给学生解释，一是让学生感悟中华古老文化的博大精深；二是给解决本题提示。）面对数十条道路众多的交叉口这个难题，我们不妨从简单的两三条道路交叉口开始，找出规律（教师边说边发放资料卡）。

三、设置问题

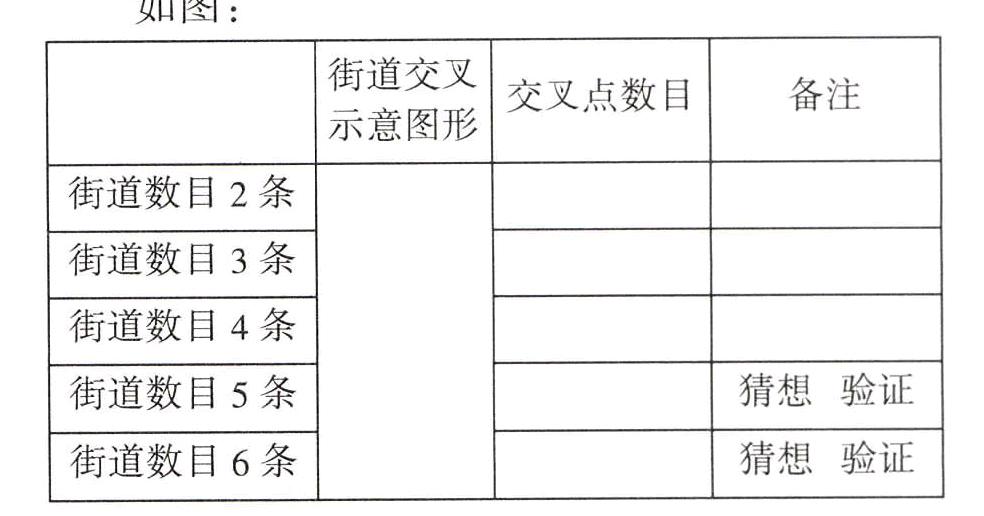
如图：

学生结合资料卡看城市交通图、道路走向及交叉位置、数目（单独操作画图，用3～5分钟。同伴交流。要求图形清晰、交叉点符合题意，用3～5分钟）。

教师组织学生交流，展示成果。

2条道路 1个交叉口。图略

3条道路 3个交叉口。图略

4条道路 6个交叉口。图略

教师关注学生交叉点数目的书写方式，提示学生注明每次增加的数目。整理为：

2条道路 1个交叉口。1

3条道路 3个交叉口。1+2

4条道路 6个交叉口。1+2+3

教师组织学生同伴交流：以2条街道交叉为起点，有1个交叉点；增加到第3条街道，和原有的2条街道都有交点，交叉点增加2个；街道增加到第4条，和原有的3条街道又都有交点，交叉点又增加3个。在这个基础上，你发现增加到第几条的街道数目和新增加的交叉点有什么关系呢？

学生：新增加的交叉点比增加到第几条的街道数目少1。

教师：我们利用这个关系猜想一下，增加到第5条街道，要增加几个交叉口？第6条呢？

学生：增加到第5条街道，要增加4个交叉口。一共是1+2+3+4=10。

增加到第6条街道，又要增加5个交叉口。一共是1+2+3+4+5=15。

教师：我们的猜想正确吗？画图验证。

（学生画图，教师巡视，指导。完成验证。）

教师：我们这个城市有20条大的街道，它们每条街道互相都有交叉口，你能利用我们发现的规律计算出最多需要多少红绿灯吗？说一说你是怎么想的，计划怎样解决问题。

学生：每增加一条街道都和原有的街道产生交叉点，我们假设新增加的街道数目为第n条，就要新增加交叉点n-1个，总的交叉口就是依次累加的总和。

学生：可以归纳为：一共20条街道，就是从1+2+3+4+……+19，计算。1+2+3+……+19=190个

教师：我们能把发现总结成结论并用字母式表示吗？

（学生同伴讨论1～3分钟。）

教师组织展示：归纳用字母n表示增加到的街道数目，最后增加的交叉口数目是n-1个。列式为：1+2+3+……（n-1）

四、导入教材解决问题

教师：出示人教版六年级数学下册课本第100页“数学思考”。

6个点可以连多少条线段？8个点呢？

教师：我们参照教科书的提示，结合我们刚才的探索，怎样解决这个问题？有什么办法呢？

（3～5分钟独立思考，然后同伴交流1～3分钟，板书演示。）

学生：结合教科书以及我们的探索发现，和上面的问题相似：2个点连接1条线段；第3个点和原有的2个点连接，增加2条线段就有3条线段；第4个点就要和原有的3个点连接，又增加3条线段就有6条线段，也就可以应用：1+2+3+……（n-1）解决问题。

学生：6个点连接：1+2+3+4+5=15条线段。8个点连接：1+2+3+4+5+6+7=28条线段。

（巩固提高）

教师：你知道12个点。20个点连接多少条线段吗？n个点呢？你能列式表示吗？猜想一下。

学生：12个点连接：1+2+3+4+……+11。20个点连接：1+2+3+4+……+19。n个点连接：1+2+3+4+……+（n-1）。

教师：大家有不同的认识吗，提出来大家分享。

学生：我赞同这样的解决问题的思路，不过，我有一个不同的推测，还不是很成熟的想法。

我用金字塔的形式表示，从最高处（最大的数）开始，比如说教材上第一个问题6个点。第6个点和下面的5个点分别连接成5条线段；第5个点又和下面的4个点连接成4个线段；第4个点又和它下面的3个点连接成3个线段；第3个点和它下面的2个点连接成2条线段；第2个点和它下面的1个点连接成1条线段；最后一个是基点。总起来就是：5+4+3+2+1=15条线段。如果用字母n表示最大的点数，那么连接的线段数就可以用式子：（n-1）+（n-2）+（n-3）+（n-4）+……表示，不知道大家赞同不，希望大家帮我验证。

教师：首先我非常赞成他的想法和推理，我们大家和他一起验证。

五、教学反思

这节课从几方面概括：①体现了课标要求的课堂教学以学生为主体的教育理念；②基本实现了解决问题从易到难阶梯式的进步；③基本上实现了对学生的全方位关注，使其得到不同程度的发展；④实践了数学来源于生活的本质，感悟了中华古老文化的博大精深。

存在的困惑：①数学语言不够精准，教师语言啰嗦；②师生交流有余，生生交流不足，不时地就有越位的冲动，老怕学生做不好，教师代办代言；③对学困生的关注心有余而力不足，特别是方法上的欠缺，暴露了教师功力的不足。