关于完全完备分配格上矩阵相对于特征值的特征向量

高元元,吴妙玲,韩凤,薛英

(内蒙古工业大学理学院数学系,内蒙古呼和浩特　010051)



关于完全完备分配格上矩阵相对于特征值的特征向量

高元元,吴妙玲,韩凤,薛英

(内蒙古工业大学理学院数学系,内蒙古呼和浩特010051)

摘要：借助于伪补和矩阵的幂序列研究了完全完备分配格上矩阵相对于特征值的特征向量的计算方法,利用特征向量的性质证明了最大特征向量的计算公式,并给出了一般特征向量的计算方法.

关键词：完全完备分配格;特征值;特征向量

1　引言

对古典线性问题: Ax =λx的研究由来已久,其中A是数域上的矩阵,在物理、力学、材料、电学、工程技术、哲学等学科中的许多问题都归结为求矩阵的特征值和特征向量.如工程技术中的振动问题和稳定问题、傅立叶变换对应的频率谱问题、求概率分布的功率谱密度、统计上的主成分分析、微分方程的特征函数以及一个物理系统的物理特性也是由表示该系统矩阵的特征值以及特征向量所决定. 20世纪六十年代以来,人们发现许多问题可以转化为格上矩阵的特征值和特征向量,其中分配格上矩阵的特征值和特征向量尤为重要.分配格是格论中重要的格,分配格上矩阵的特征值和特征向量在计算机理论、范畴论、密码学、拓扑代数和模糊数学等学科中有着广泛的应用.研究分配格上矩阵的特征值-特征向量,主要考虑以下三个方面的问题:

(1)给定分配格上矩阵的特征向量,如何确定矩阵的相对于特征向量的特征值.

(2)给定分配格上矩阵的特征值,如何确定矩阵的相对于特征值λ的特征向量.

(3)给定分配格上一个向量ξ及一个数λ,如何确定以ξ为特征向量并以λ为特征值的矩阵A.

关于问题(1), Rutherford指出:给定Boolean代数上的矩阵A及特征向量,相对应的特征值构成Boolean代数上的一个区间,并给出这个区间的计算公式.后来文献[1]把这个结论推广到完全完备的分配格上,也得出类似的结论.对于问题(2), Rutherford证明了对于Boolean代数上的矩阵A, Boolean代数中的任一元都是A的特征值,且矩阵A的相对于特征值的特征向量构成一个子空间,并给出了子空间中最大特征向量的计算公式.对于问题(3), Blyth证明了以ξ为特征向量且以λ为特征值的分配格上的矩阵构成一个Gerbier (即V -半网状-半群),并给出Gerbier中的最大矩阵的计算公式[1].本文在前人的基础上,对完全完备分配格上矩阵的特征向量进行了研究,介绍了完全完备分配格上矩阵的特征向量的性质,指出与特征值λ对应的特征向量构成一个子空间,并给出最大特征向量的求解公式,又进一步介绍了一般特征向量的计算方法.

完全完备分配格是分配格,所以文中关于分配格的结论对于完全完备分配格同样适用.

2　预备知识

定义2.1设L是一个格, a,b∈L,满足不等式a∧x≤b的最大值x∈L被称为a在b中的相对伪补,记为a→b,对于格L中的任意两个元素a,b,有

定义2.2设L = 为格,如果L满足:

(1)格L的每个非空子集S都有一个下确界和一个上确界;

文中格L是完全完备分配格,有最大元1及最小元0,记a′= a→0,a′′= (a′)′,

是L中的一个区间.

集合Vn(L)是L上所有的列向量组成的一个完全完备分配格,设0 = (0,···,0)T及e = (1,···,1)T.对任意的ξ,η∈Vn(L),i = 1,2,···,n,ξ≤η⇐⇒ξi≤ηi,格上向量的运算为:

L上的n×n矩阵的集合Mn(L)组成一个完全完备分配格,对任意的矩阵

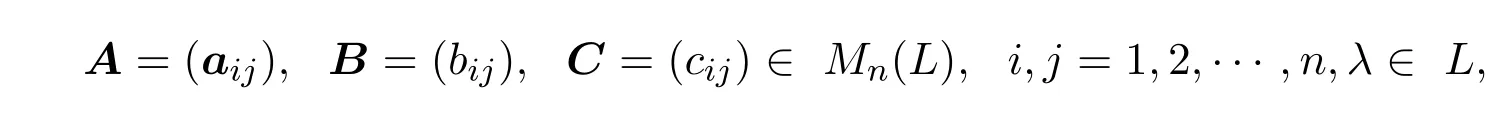
格上矩阵的运算为:

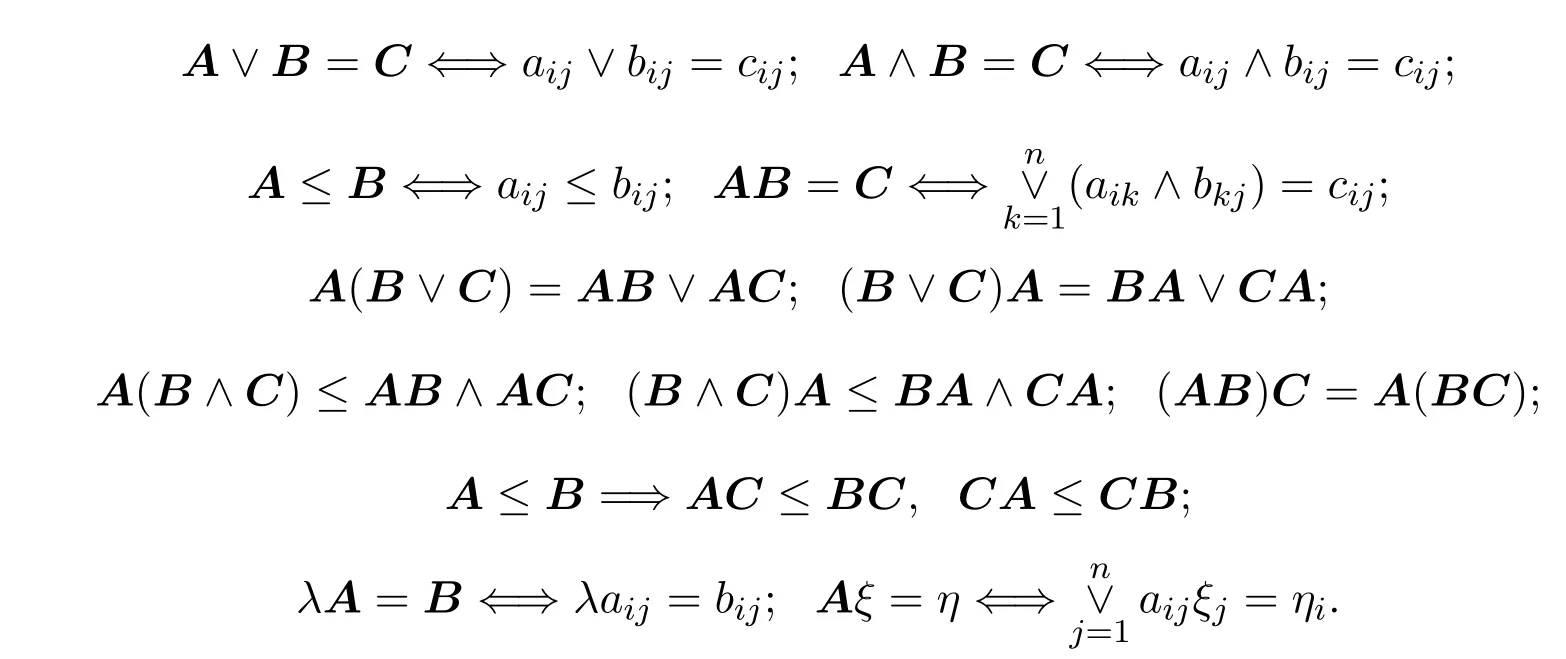
引理2.1[3]对任意的a,b∈L,(a→b)∧b′≤a′.

引理2.2[3]对任意的ξ,η,ζ,α1,···,αn∈Vn(L),有

引理2.3[3]对任意的a,b,c∈L,有

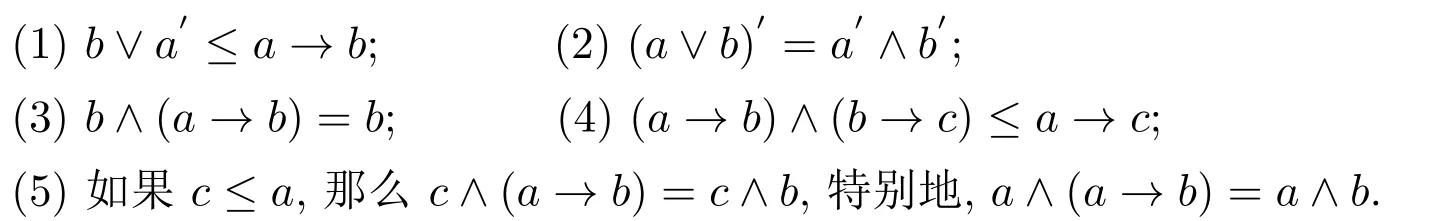
引理2.4[3]对任意的A∈Mn(L),A(ATe)′= 0.

引理2.5[3]设A = (aij)∈Mn(L),λ∈L且λ′∨λ= 1,ξ= (x1,···, xn)T∈Vn(L),如果λAξ= 0,那么

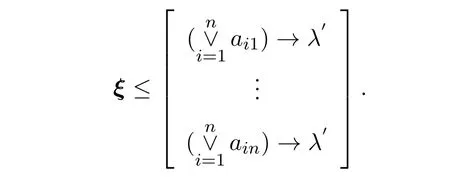
引理2.6[4]设A∈Mn(L),令A(k)= Ak∨···∨Ak+n−1,k≥1,则对任意的k≥n,

有A(k)= A(n).

引理2.7[5]设λ∈L,如果λ′∨λ= 1,那么λ′′=λ.

3　特征向量的性质

定理3.1设A∈Mn(L),λ是矩阵A的特征值,那么λ的所有特征向量构成Vn(L)的一个子空间E(A,λ),且存在最大的特征向量和最小的特征向量.

证明如果Aξ=λξ,Aη=λη,那么

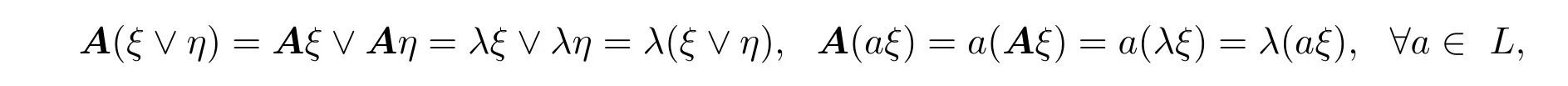
从而λ的特征向量构成Vn(L)的子空间E(A,λ),其中最大特征向量ξ∗是所有特征向量的并,最小特征向量是0.

定理3.2设A∈Mn(L),λ是矩阵A给定的特征值,那么(1)ξ∗(λ) = (λe∨ATe)→(λAne);

(2)如果λ满足λ′∨λ= 1,那么ξ∗(λ) =λAne∨λ′(ATe)′.证明(1)

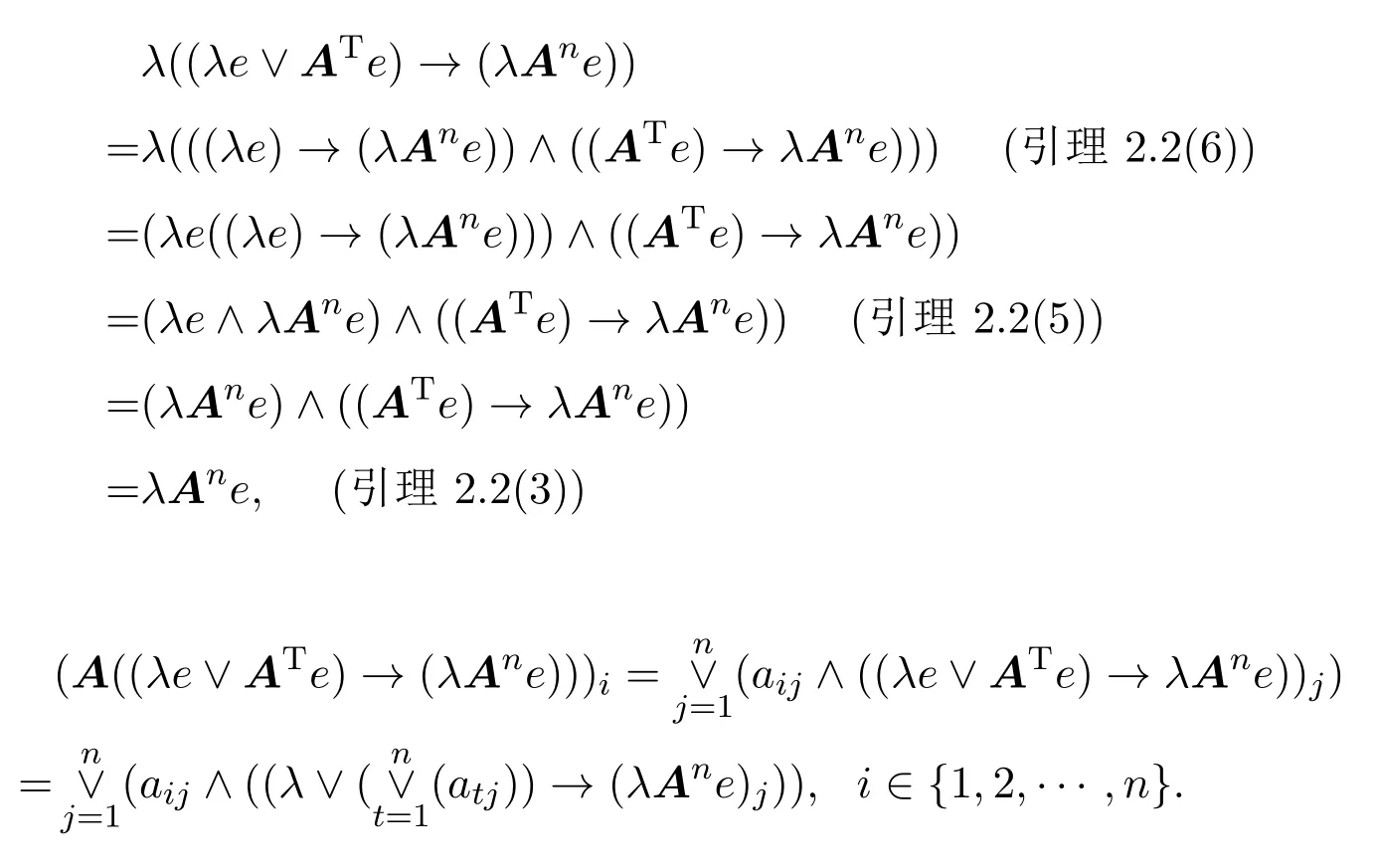
那么

因此

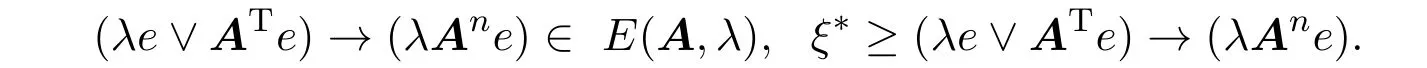
设∀ξ∈E(A,λ),那么Aξ=λξ,则λξ=λAnξ≤λAne,因此ξ≤(λe)→(λAne).

一方面,∀i,j = 1,2,···,n,当Aξ=λξ⇐⇒(Aξ)i=λ∧ξi,有aij∧ξj≤λ∧ξi≤λ, 且ξj≤aij→λ,因此有

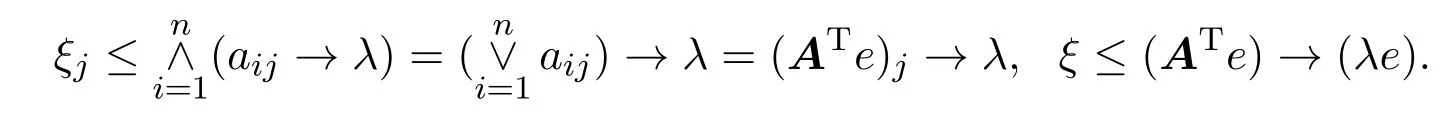
因此,

ξ≤((ATe)→(λe))∧((λe)→(λAne))≤(ATe)→(λAne) (引理2.2(4)), 且ξ≤((λe)→(λAne))∧((ATe)→(λAne)) = (λe∨ATe)→(λAne))(引理2.2(6)),因此ξ∗(λ) = (λe∨ATe)→(λAne).

(2) A(λAne∨λ′(ATe)′) =λAn+1e∨λ′A(ATe)′=λAne =λ(λAne∨λ′(ATe)′)(由引理2.4),因此ξ∗(λ)≥λAne∨λ′(ATe)′.

如果Aξ=λξ,那么λ′Aξ=λ′λξ= 0,由引理2.5及引理2.7有

由引理2.1得

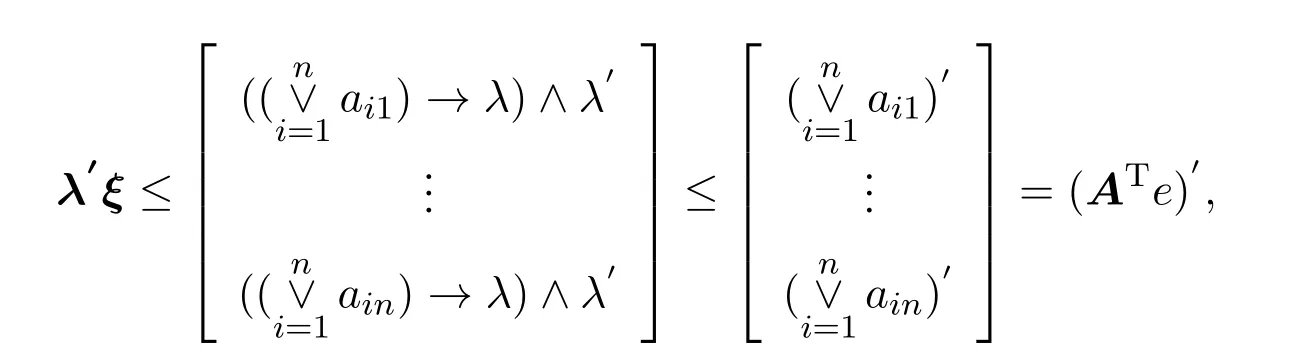
因此,λ′ξ≤λ′(ATe)′.

另一方面, A(λξ) =λAξ=λλξ=λξ,因为ξ≤Anξ≤Ane,从而λξ≤λAne,因此ξ= (λ∨λ′)ξ=λξ∨λ′ξ≤λAne∨λ′(ATe)′,且ξ∗(λ)≤λAne∨λ′(ATe)′,从而可得ξ∗(λ) =λAne∨λ′(ATe)′.

4　特征向量的计算

定理3.2已经给出矩阵相对于特征值λ的最大特征向量的求解公式,那么如何求解相对于特征值λ的一般的特征向量?

λ= 1的特征向量称为标准特征向量,如果x是矩阵A的一个标准特征向量,那么对于任意的λ∈L,λx必为矩阵A的关于特征值λ的一个特征向量.这是因为

因此求解一般特征向量,只需会解标准特征向量即可.下面介绍分配格上矩阵的标准特征向量的求法.

定理4.1 A为分配格L上的n×n矩阵, AX = X,当且仅当X = A(n)Y,∀Y∈Ln, 即X = A(n)Y为A的全部标准特征向量.

证明由A(B∨C) = AB∨AC,可得

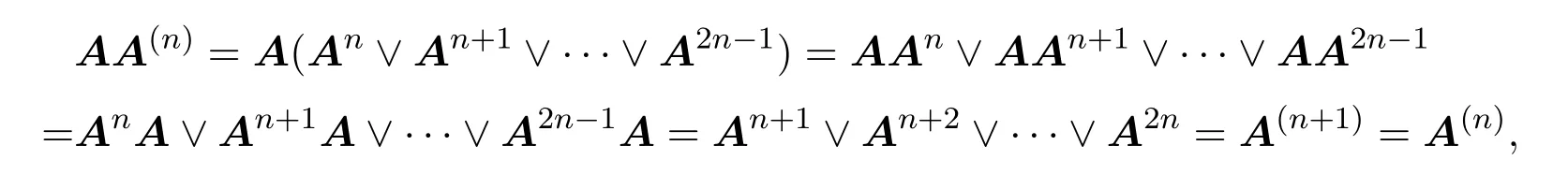
所以AA(n)Y = A(n)Y知A(n)Y是A的一个标准特征向量.

又因为X = AX =⇒X = A(n)X = A(n)Y (取X = Y ),可以看到每一个特征向量X都可以表示成A(n)Y的形式,所以X = A(n)Y为A的全部标准特征向量.

推论4.1 A为完全完备分配格上的n×n矩阵,则X =λA(n)Y为A的对应于λ的特征向量.

结合以上求解特征向量的方法,给出下面的例子.

例4.1如图1所示,格L = {0,a,b,c,d,1},由定义2.2可知L是一个完全完备分配格. 设

那么ATe = (1,1,1)T,A3e = (1,b,1)T.

由定理3.2(1)的公式ξ∗(λ) = (λe∨ATe)→(λAne),可得

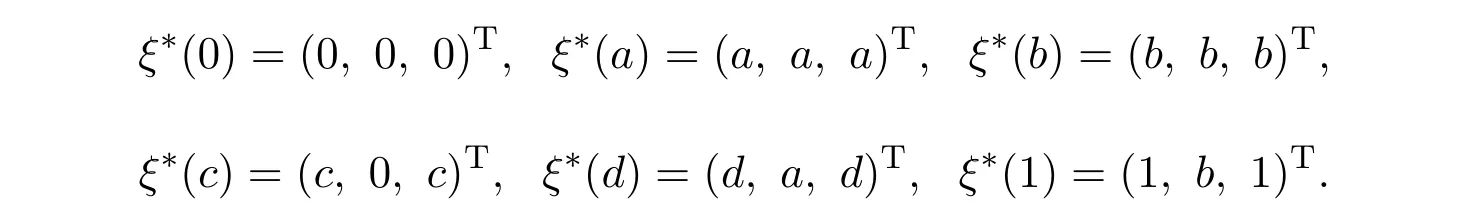
当λ= 1时,λ′= 0,且λ′∨λ= 1,根据定理3.2(2)的公式ξ∗(λ) =λAne∨λ′(ATe)′,从而可得ξ∗(1) = (1 b 1)T, (与定理3.2(1)得出的结果一样).

再根据推论4.1求解矩阵相对于特征值λ的特征向量X ,其中X =λA(n)Y .

给定特征值λ= d,可得

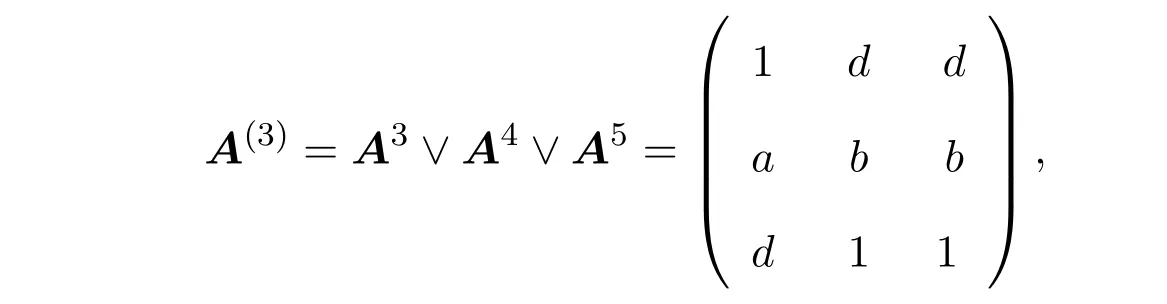
由于Y是任意的,可以取Y = e,则X =λA(3)Y = (d,a,d)T(与定理3.2(1)所得结果一样).

参考文献

[1] Tan Yijia. On generalized fuzzy matrices with period [J]. Fuzzy Sets And Systems, 2011,172:87-103.

[2]陈杰.格伦初步[M].呼和浩特:内蒙古大学出版社, 1988.

[3] Blyth T S. On eigenvectors of Boolean matrices [J]. Pro. Roy. Soc. Edinburgh Sect. A, 1966,67(3):196-204.

[4]范周田.模糊矩阵理论与应用[M].北京:科学出版社, 2006.

[5] Kirkland S, Pullman N J. Boolean spectral theory [J]. Linear Algebra Appl., 1992,175(1):63-73.

MSC: 16Y60

Eigenvectors with the associated eigenvalues for matrices in a class of a complete and completely distributive lattices

Gao Yuanyuan , Wu Miaoling , Han Feng , Xue Ying
(Department of Mathematics, College of Sciences, Inner Mongolia University of Technology, Hohhot 010051, China)

Abstract:By means of the pseudocomplement and power sequence of matrix research the calculation method of the eigenvector with respect to the eigenvalues of matrix on on the complete and completely distributive lattices. Using the properties of eigenvectors proved the calculation formulas of maximum eigenvectors, and gives the method for solving general eigenvectors.

Key words:complete and completely distributive lattices lattices, eigenvalues, eigenvectors

通讯作者：吴妙玲(1964-),硕士,副教授,研究方向：格伦与模糊数学.

作者简介：高元元(1987-),硕士生,研究方向：格论与模糊数学.

基金项目：内蒙古工业大学研究生教育教学研究项目(KC2014007).

收稿日期：2014-10-23.

DOI：10.3969/j.issn.1008-5513.2016.01.013

中图分类号：O153.1

文献标识码：A

文章编号：1008-5513(2016)01-0093-07