渐近拟非扩张非自映射的收敛定理

沈德兄,郭伟平

(苏州科技学院数理学院,江苏苏州　215009)



渐近拟非扩张非自映射的收敛定理

沈德兄,郭伟平

(苏州科技学院数理学院,江苏苏州215009)

摘要：在实线性赋范空间中引入了渐近拟非扩张非自映射概念.并在Banach空间中证明了渐近拟非扩张非自映射对的强收敛定理,所得结果推广和改进了相关文献的结论.

关键词：实Banach空间;渐近拟非扩张映射;公共不动点;强收敛

1　引言及预备知识

设E是实线性赋范空间, C是E的非空子集,称T : C→C是一致L-Lipschitzian映射[1],如果存在常数L＞0,使得

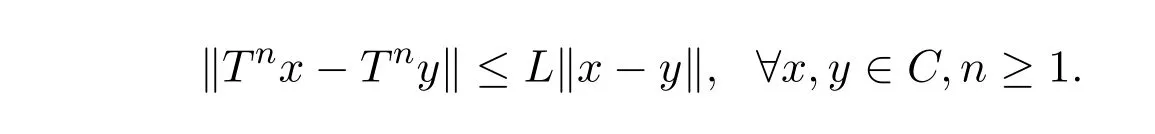
称T : C→C是渐近非扩张映射[2],如果存在实数列

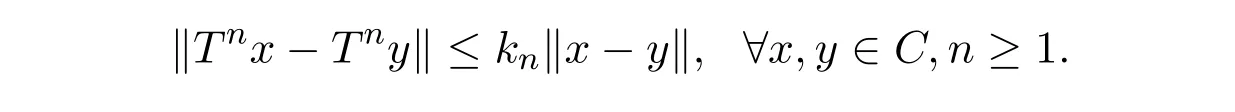
记F(T) = {x∈C : Tx = x}为T的不动点集.

称T : C→C是渐近拟非扩张映射[3],若F(T) /=∅且存在实数列

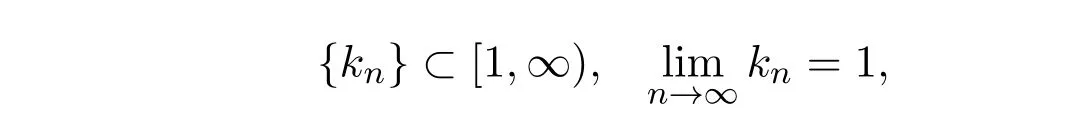
使得

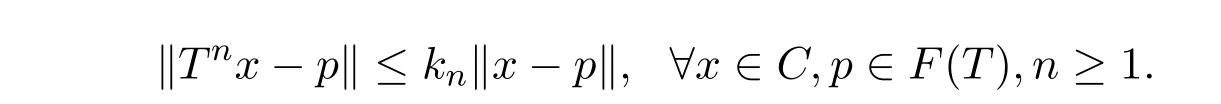
由定义可知, T为渐近非扩张映射,则T必为一致L-Lipschitzian映射,当F(T) /=∅时, T为渐近非扩张映射,则T为渐近拟非扩张映射,反之不成立.

2003年,文献[4]引入了渐近非扩张非自映射的定义,其定义如下:

定义1.1[4]设E是实线性赋范空间, C是E的非空子集,设P : E→C是E到C上的非扩张收缩映射.非自映射T : C→E称为渐近非扩张的,如果存在实数列

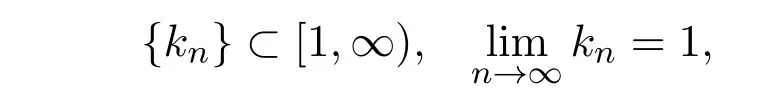
使得

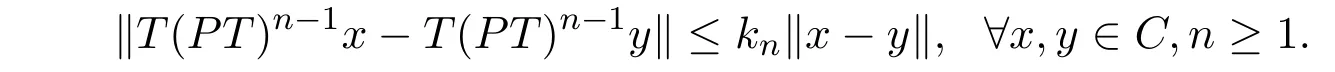
非自映射T : C→E称为一致L-Lipschitzian的,如果存在常数L＞0,使得

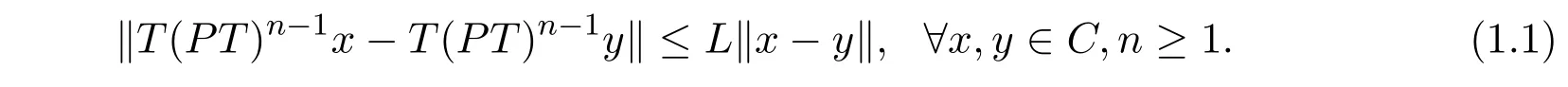
称实Banach空间E的子集C为E上的收缩集[4],如果存在连续映射P : E→C使得对于任意x∈C有Px = x.一致凸Banach空间中的每个闭凸子集都为收缩集.称映射P : E→E为收缩的,如果P2= P.换言之,如果P为可收缩的,则对于P的值域中的每个y都有Py = y.

引入新的定义如下:

定义1.2设E是实线性赋范空间, C是E的非空子集.设P : E→C是E到C上的非扩张收缩映射.非自映射T : C→E称为渐近拟非扩张的,如果F(T) /=∅且存在实数列

2007年,文献[3]引入了迭代列{xn}如下:

设C是实Banach空间E中的非空凸子集, T,S : C→C是两渐近拟非扩张映射,定义迭代列{xn}如下:

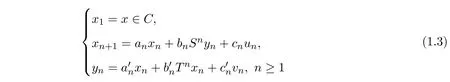
本文引入新的迭代列{xn},其定义如下:

设C是实Banach空间E中的非空凸子集, S,T : C→E为两渐近拟非扩张非自映射,定义迭代列{xn}如下:

为证明主要定理,需以下引理及条件.

引理1.1[5]设{rn},{sn},{tn}是非负实数列,且满足下列条件:

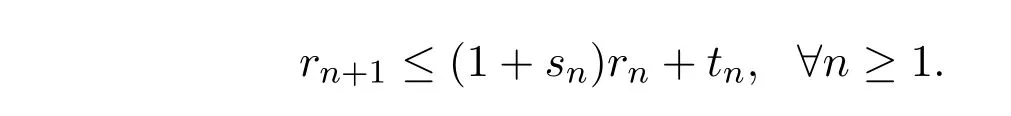
引理1.2[6]设E是实一致凸Banach空间, b,c是(0,1)上的两个常数且b＜c.设{tn} 是[b,c]中的实数列, {xn},{yn}是E中序列且满足如下条件:

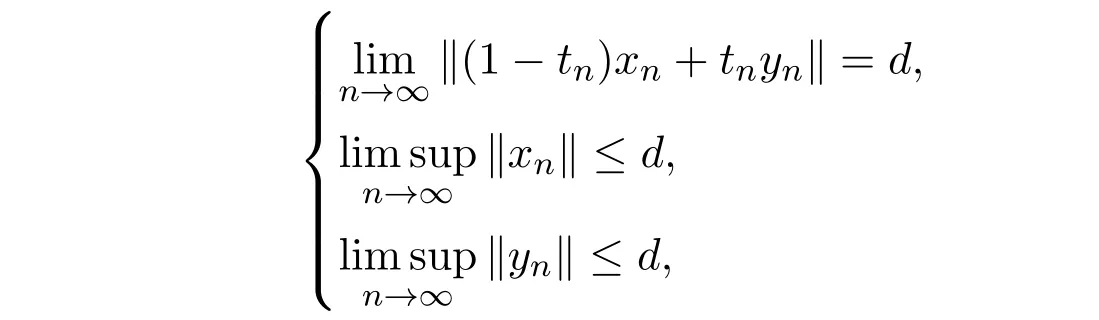
证明∀pn∈F(T)且‖pn−q‖→0,于是

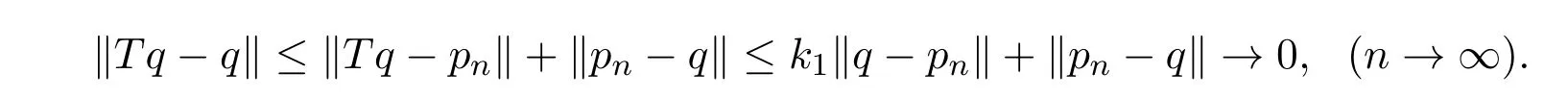
故q∈F(T).因此F(T)为闭集.

设C为实Banach空间中的非空子集,称两非自映射S,T : C→E满足条件:

(A′)如果存在非减函数f : [0,∞)→[0,∞)满足f(0) = 0且对任意r∈(0,∞) 有f(r)＞0,使得∀x∈C,有

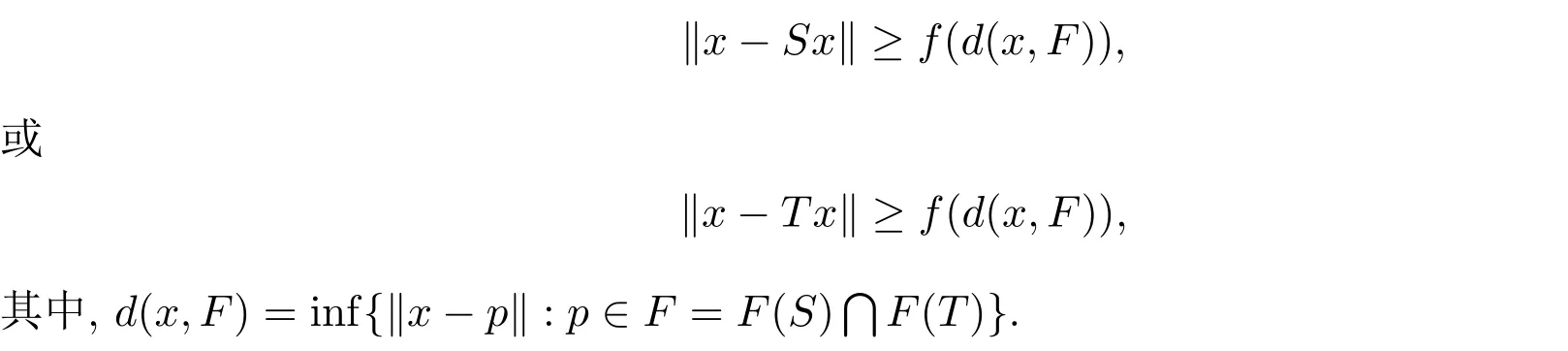
引理1.3设C是实线性赋范空间E的非空闭子集, T : C→E是具有{kn}⊂[1,∞)且

2　主要结论

本节中,在实Banach空间中证明由(1.4)式定义的迭代列的强收敛定理.

引理2.1设C是实Banach空间E的非空闭凸子集,设S,T : C→E是分别具有

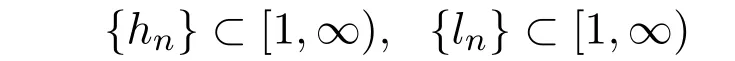
的渐近拟非扩张非自映射并且

设{xn}是由(1.4)式所定义的迭代列.其中是[0,1]上的六个实数列且满足

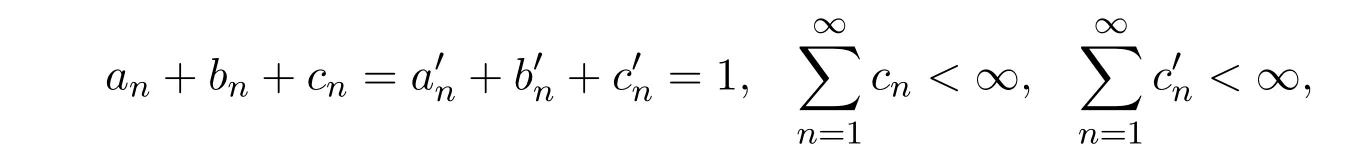
{un},{vn}是C上的两个有界序列.若则∀p∈F,极限存在.

证明给定p∈F,由{un},{vn}的有界性知存在M＞0,使得

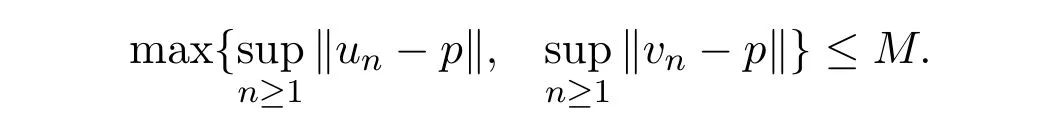
记kn= max{hn,ln},由(1.4)式知

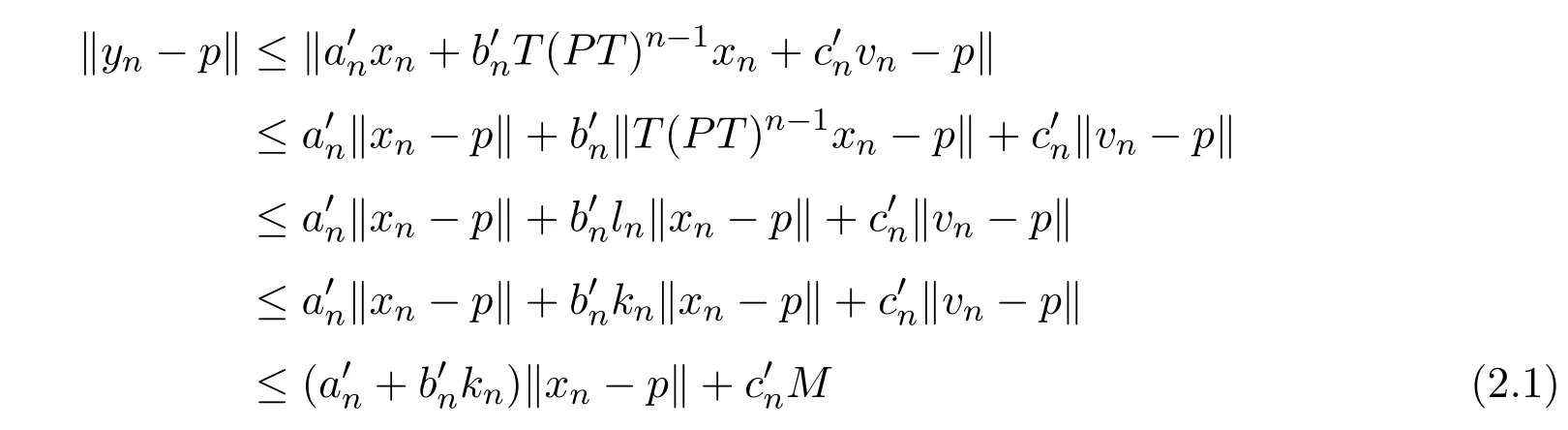
且

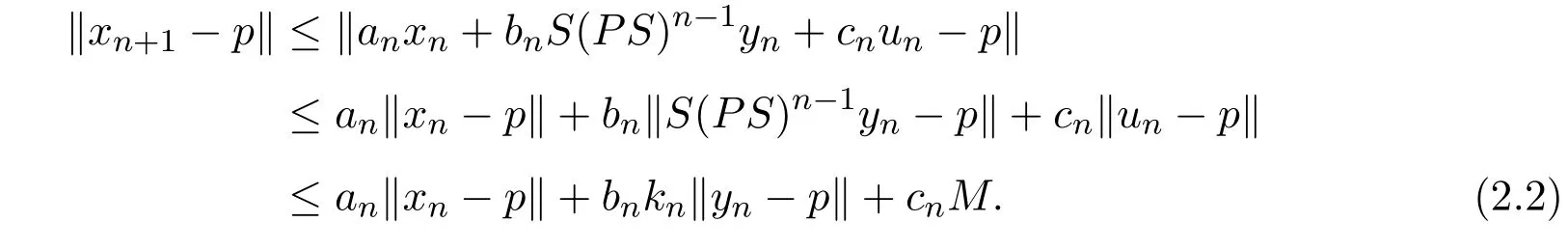
将(2.1)式代入(2.2)式得到

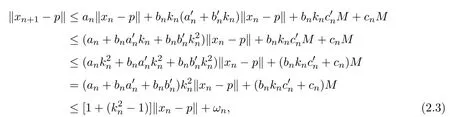
引理2.2设C是实Banach空间E的非空闭凸子集, S,T : C→E分别有{hn}⊂[1,∞), {ln}⊂[1,∞)的渐近拟非扩张非自映射并且

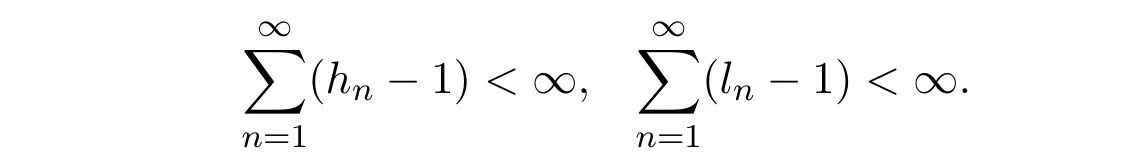
设{xn}是由(1.4)式所定义的迭代列,其中是[0,1]上的六个实数列且

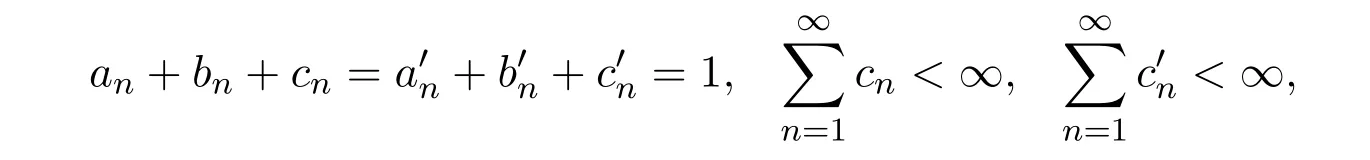
{un},{vn}是C上的两个有界序列.若F = F(S)∩F(T) /=∅,则存在R＞0,使得∀p∈F, 有

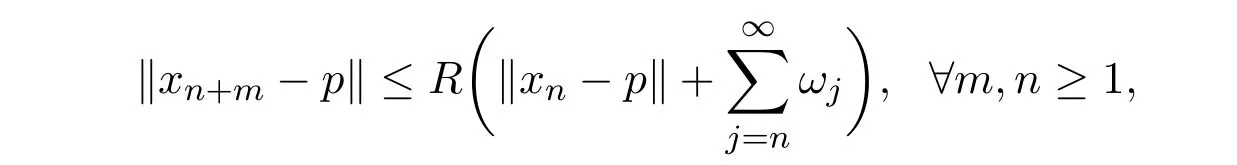
其中,ωj= [cj+ bjc′jkj]M.

证明由引理2.1知

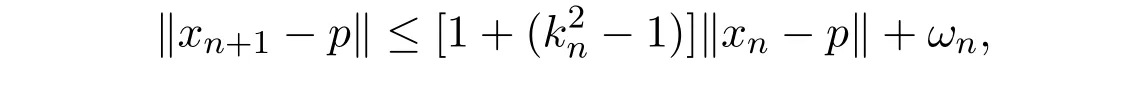
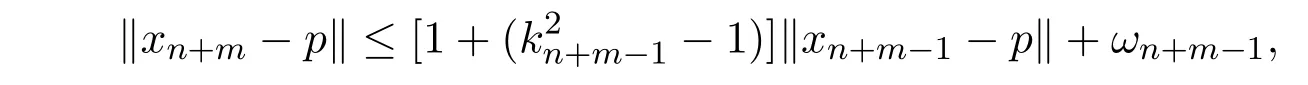
令αj= k2j−1,(j≥1),故由上式可得到

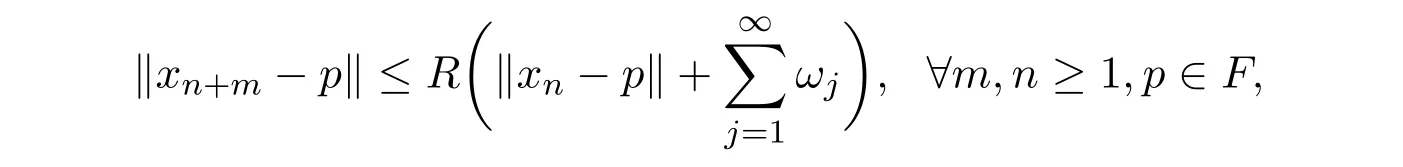
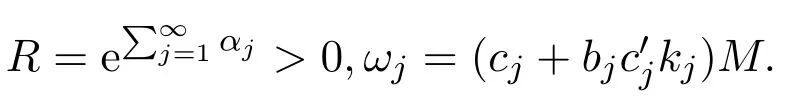
下面证明本文中主要定理.

定理2.1设C是实Banach空间E的非空闭凸子集, S,T : C→E分别有{hn}⊂[1,∞), {ln}⊂[1,∞)的渐近拟非扩张非自映射并且

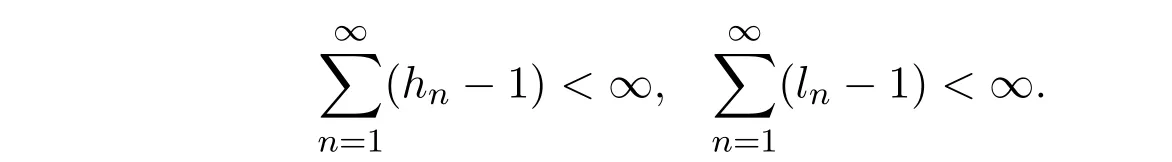
设{xn}是由(1.4)定义的迭代列,其中是[0,1]上的六个实数列且满足

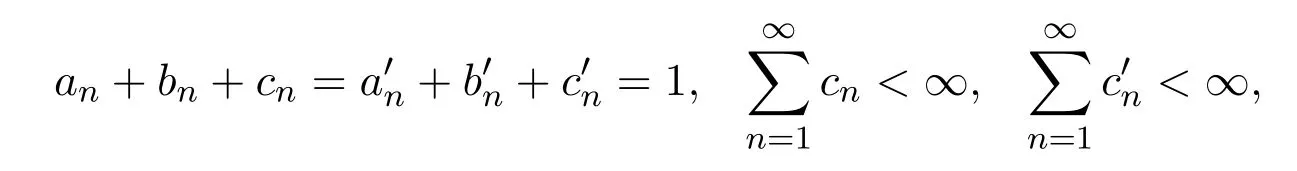
{un},{vn}是C上的两个有界序列.若F = F(S)∩F(T) /=∅,则{xn}强收敛到S,T的公共不动点的充要条件是

证明设kn= max{hn,ln}.必要性是显然的,只需证明充分性.设由引理2.1知

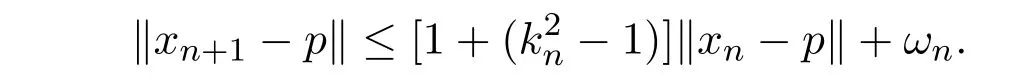
故d(xn+1,F)≤[1 + (k2n−1)]d(xn,F) +ωn,又由于

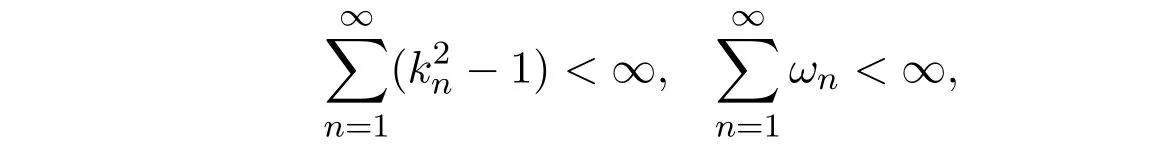
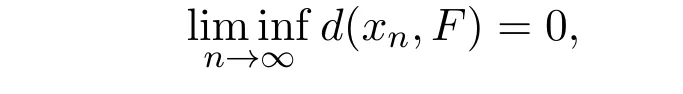
现在证{xn}是柯西列.∀ε＞0.由于因此存在n0使得当n≥n0时,有

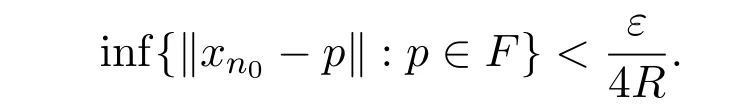
故存在p∗∈F使得于是当n≥n0,∀m≥1时,由引理2.2知

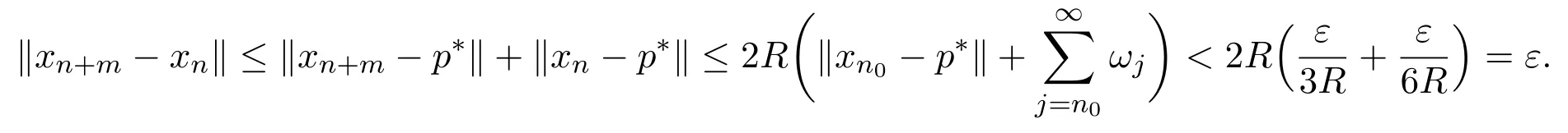
因此{xn}是柯西列.又由于C是实Banach空间E的闭子集.故必存在一点q∈C使得故d(q,F) = 0.由引理1.3知F是闭的,故q∈F.

定理2.2设C是实一致凸Banach空间E的非空闭凸子集,设S,T : C→E是分别具有{hn}⊂[1,∞),{ln}⊂[1,∞)的一致L-Lipschitzian渐近拟非扩张映射且

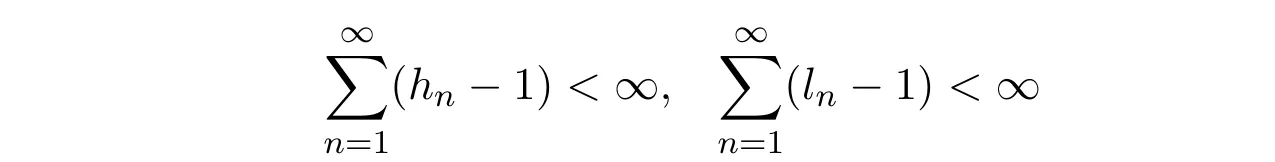
满足条件(A′).设{xn}是由(1.4)所定义的迭代列,其中是[0,1]上的六个实数列且满足

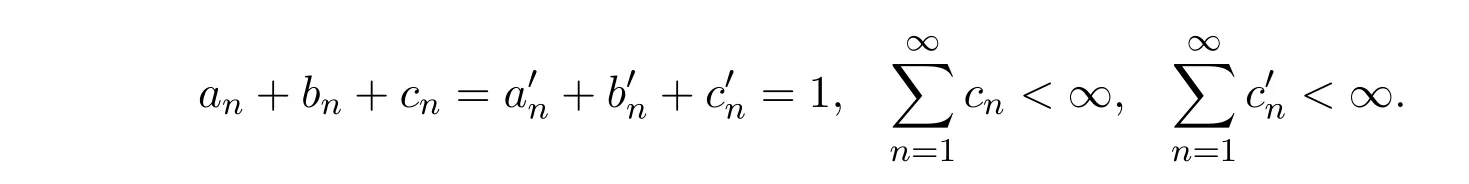
由(1.4)式知

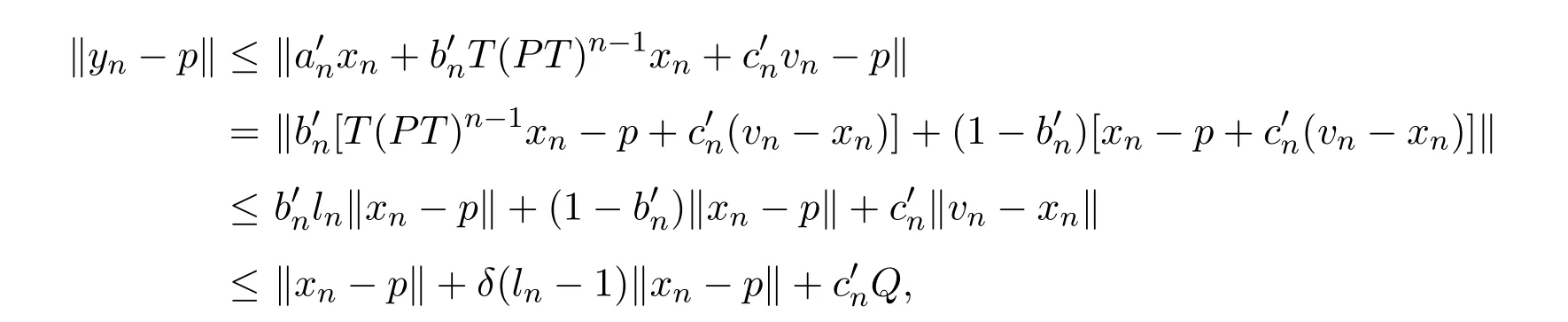
两边同时取上极限,则有

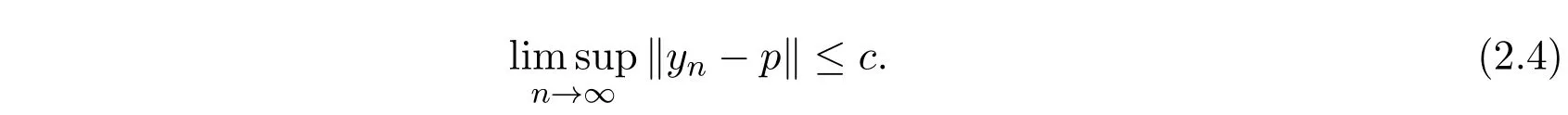
注意到‖S(PS)n−1yn−p + cn(un−xn)‖≤hn‖yn−p‖+ cnQ.故

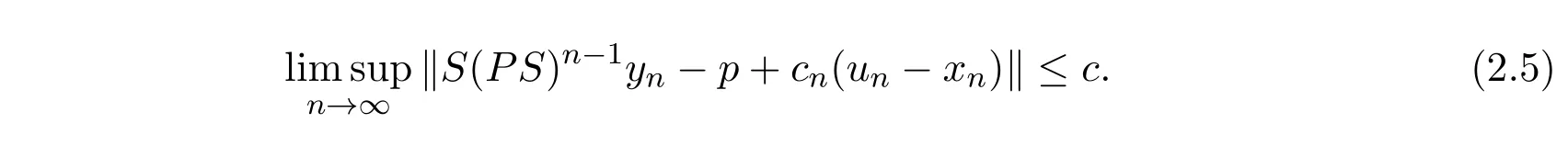
同时‖xn−p + cn(un−xn)‖≤‖xn−p‖+ cnQ.从而

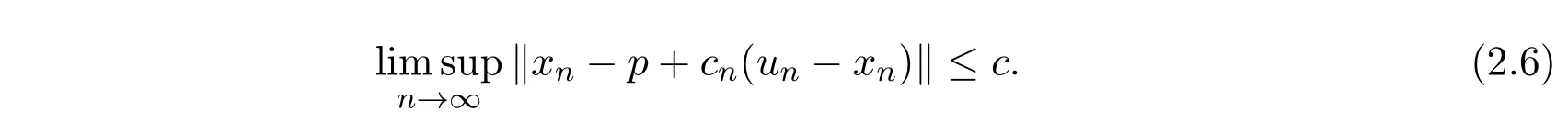
由(2.1)式和(2.3)式知

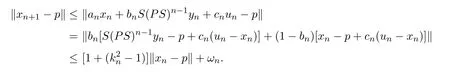
再由limn→∞‖xn+1−p‖= c.故

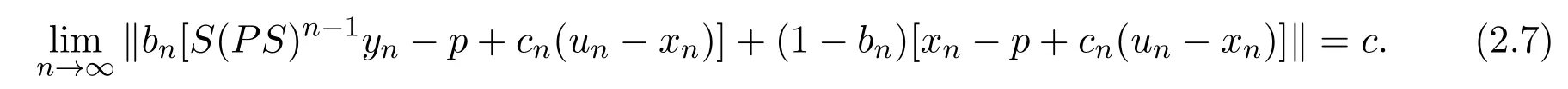
由引理1.2及(2.5)-(2.7)式知

因为

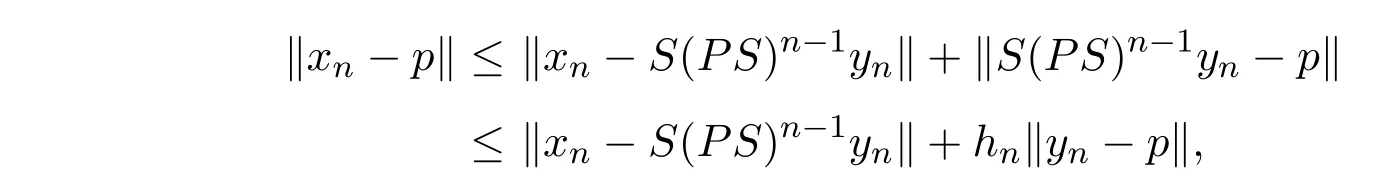
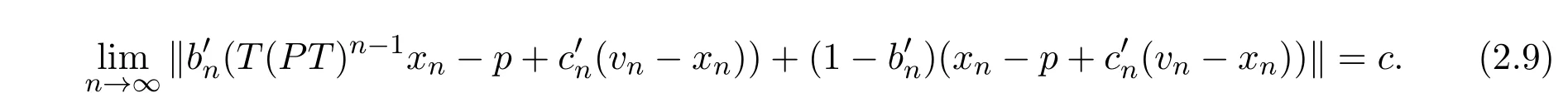
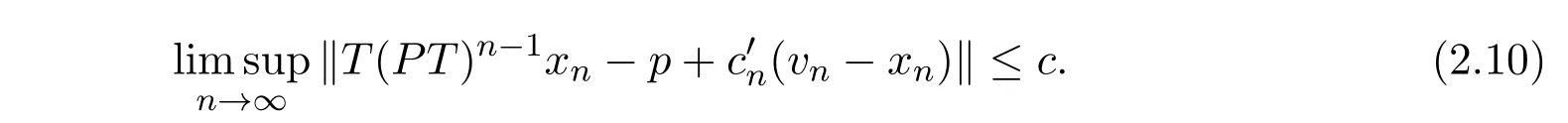
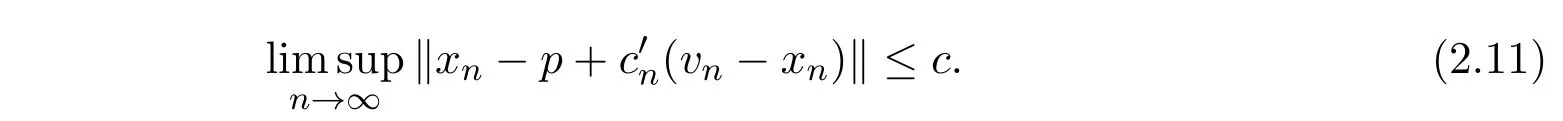
再由引理1.2及(2.9)-(2.11)式可知

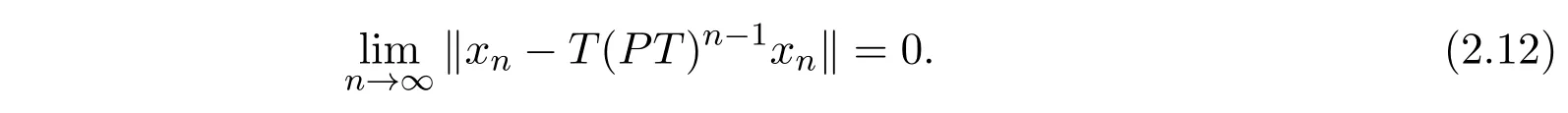
又

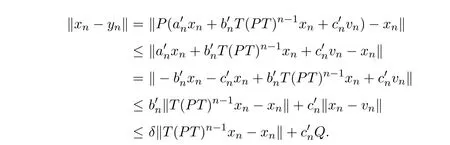
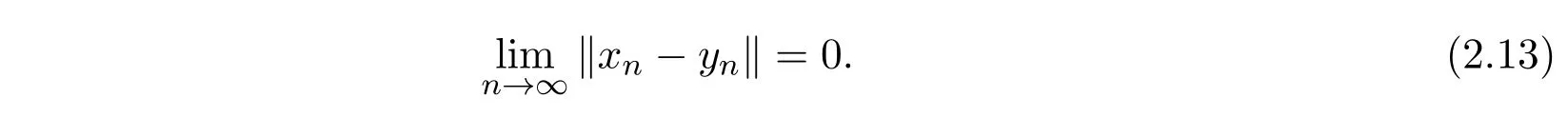
由S为一致L-Lipschitzian映射,有

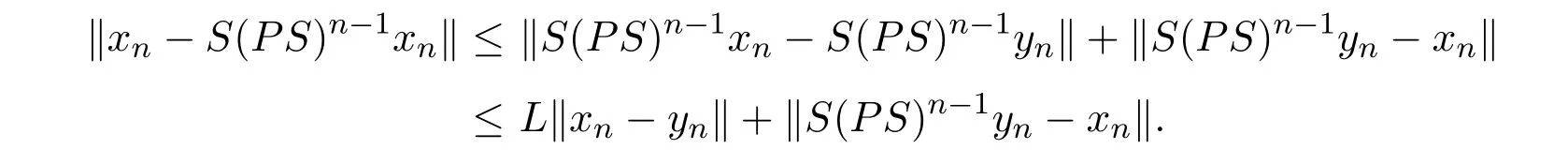
由(2.8)式与(2.13)式知

又

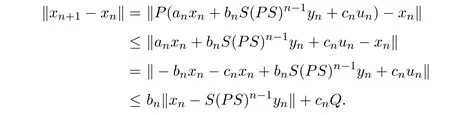
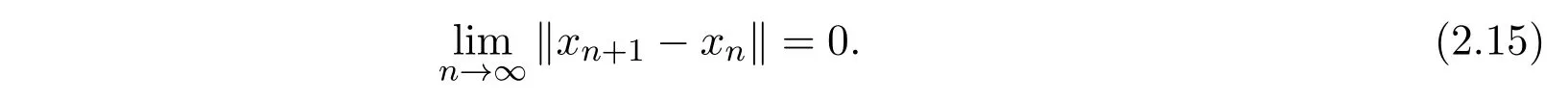
又

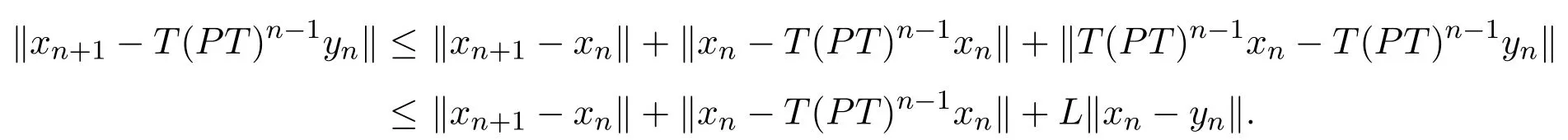
由(2.12),(2.13)和(2.15)式知

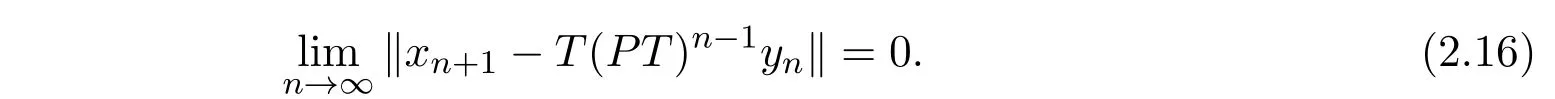
从而

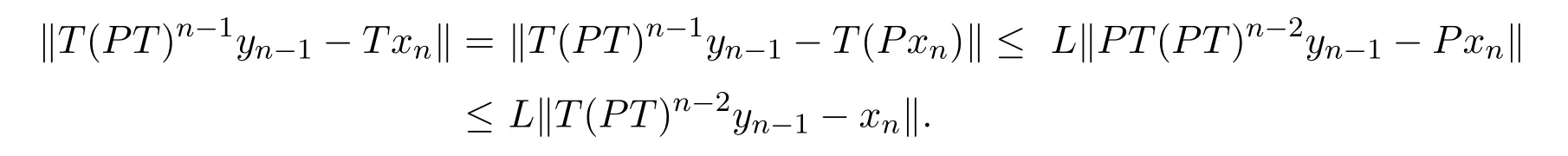
由(2.16)式知

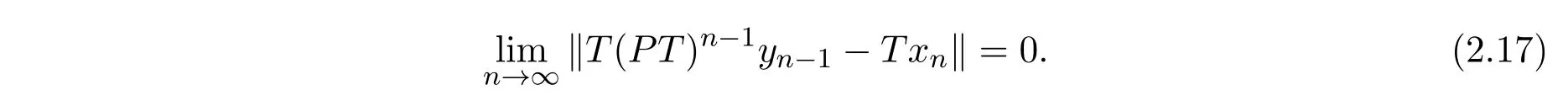
又

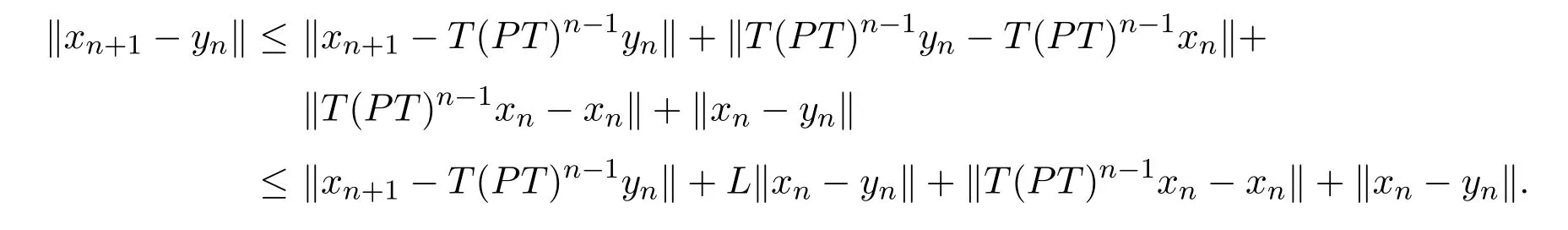
由(2.12),(2.13)和(2.16)式知

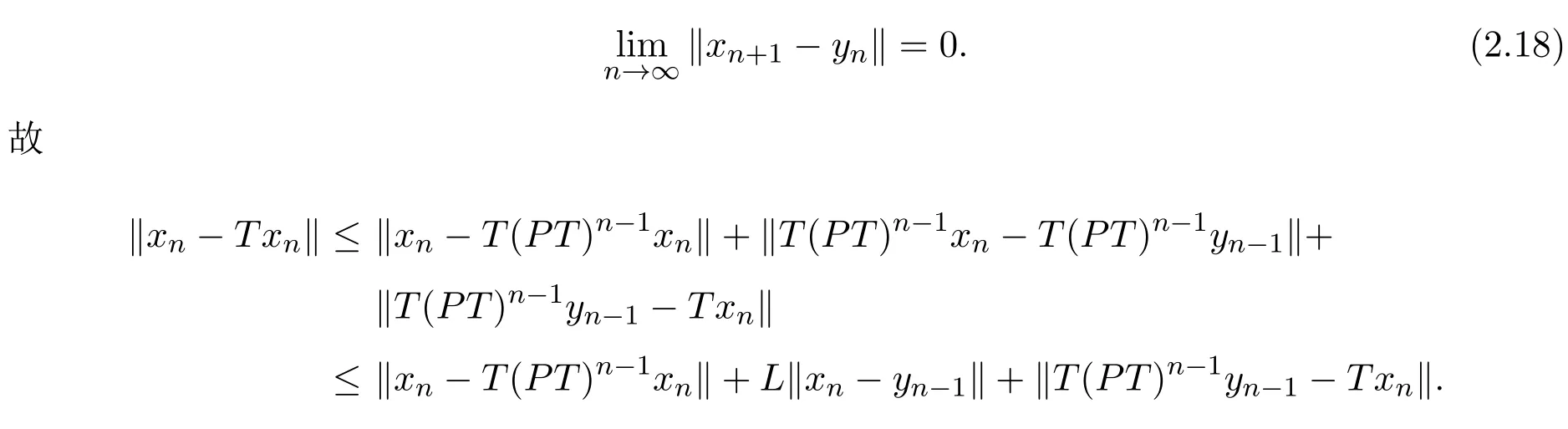
由(2.12),(2.17)和(2.18)式知

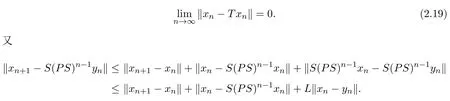
由(2.13),(2.14)和(2.15)式知

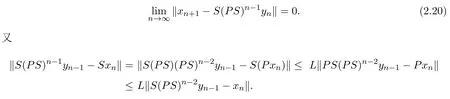
由(2.20)式知

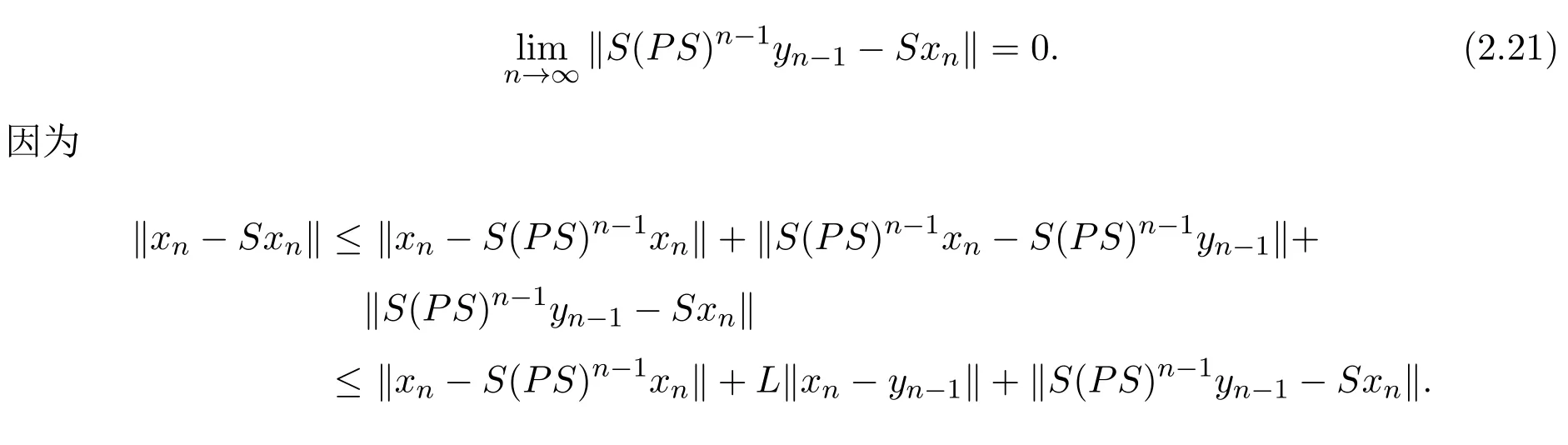
由(2.14),(2.18)和(2.21)式知

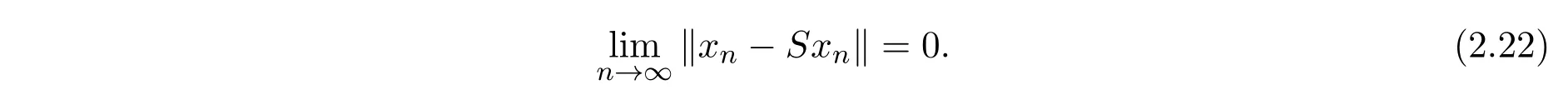
由条件(A′),(2.19)及(2.22)式知

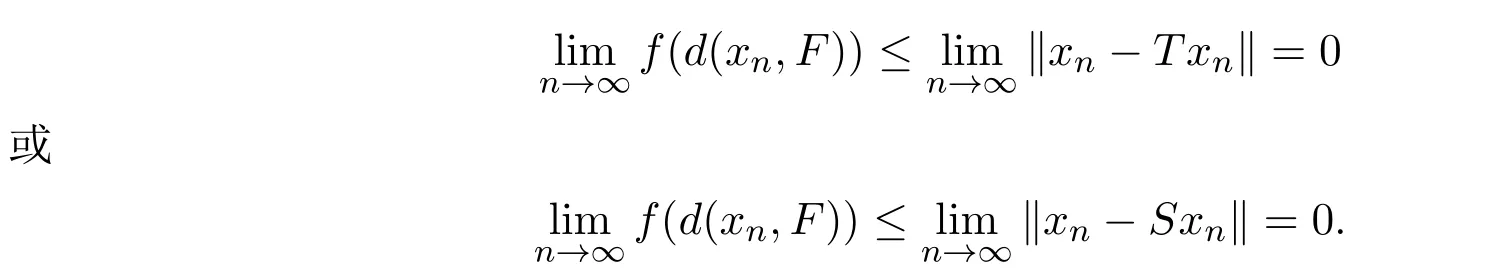
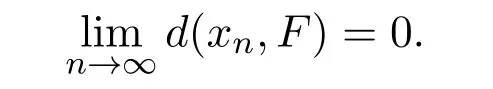
再由定理2.1知{xn}强收敛到S,T的公共不动点.

注记2.1定理2.2将文献[3]中的定理2中的自映射的强收敛定理推广到了非自映射的强收敛定理.

参考文献

[1] Schu J. Iterative construction of fixed point of asymptotically nonexpansive mappings [J]. J. Math. Anal. Appl., 1991,158:407-413.

[2] Goebel K, Kirk W A. A fixed point theorem for asymptotically nonexpansive mapping [J]. Proc. Amer. Math. Soc., 1972,35:171-174.

[3] Hafiz Fukharuddinj, Safeer Hussain Khan. Convergence of iterates with errors of asymptotically quasinonexpansive mappings and applications [J]. J. Math. Anal. Appl., 2007,328:821-829.

[4] Chidume C E, Ofoedu E U, Zegeye H . Strong and weak convergence theorems for asymptotically nonexpansive mappings [J]. J. Math. Anal. Appl., 2003,280:364-374.

[5] Sun Z H. Strong convergence of an implict iteration process for a finite family of asymptotically quasinonexpansive mappings [J]. J. Math. Anal. Appl., 2003,286:351-358.

2010 MSC: 47H09, 47H10, 47J25

[6] Schu J. Weak and strong convergence of fixed points of asymptotically nonexpansive mappings [J]. Bull. Aust. Math. Soc., 1991,43:153-159 .

Convergence theorems for asymptotically quasi-nonexpansive non-self mappings

Shen Dexiong , Guo Weiping
(College of Mathematics and Physics, Suzhou University of Science and Technology, Suzhou 215009, China

Abstract:In this paper ,we introduce a new two-step iterative scheme of two asymptotically quasi-nonexpansive nonself-mappings in real normed linear space and prove strong convergence theorems for the new two-step iterative scheme in Banach spaces. The obtained results in this paper improve and extend some corresponding results.

Key words:Banach space, asymptotically quasi-nonexpansive mapping, common fixed point, strong convergence

作者简介：沈德兄(1991-),硕士生,研究方向：非线性泛函分析.

基金项目：国家自然科学基金(11271282).

收稿日期：2015-04-20.

DOI：10.3969/j.issn.1008-5513.2016.01.014

中图分类号：O177.91

文献标识码：A

文章编号：1008-5513(2016)01-0100-11