模糊值m-凸函数的性质及其共轭问题的研究
廖甲根,杜廷松,2
(1.三峡大学理学院数学系,湖北宜昌 443002 2.武汉科技大学冶金工业过程系统科学湖北省重点实验室,湖北武汉 430081)
模糊值m-凸函数的性质及其共轭问题的研究
廖甲根1,杜廷松1,2
(1.三峡大学理学院数学系,湖北宜昌443002 2.武汉科技大学冶金工业过程系统科学湖北省重点实验室,湖北武汉430081)
摘要:基于m-凸函数提出了一类称为模糊值m-凸函数的新概念.首先,研究了模糊值m-凸函数的若干基本性质;其次,给出了模糊值m-凸函数的共轭函数的概念,并给出了模糊值m-凸函数在一定的条件下的共轭函数是模糊值m-凸函数等相关性质;最后,讨论了两个模糊值m-凸函数的共轭函数与其下卷积的共轭函数之间的相互关系.
关键词:模糊值m-凸函数;共轭函数;下卷积
1 引言
自1972年文献[1]首次提出模糊集的概念以来,其理论研究已有了很大的进展,并得到广泛的应用.而模糊凸分析,作为模糊优化理论研究的基础,已成为模糊数学的重要分支.例如,文献[2]给出了基于模糊数空间的一种新的序关系下的可微凸模糊数值函数、拟凸模糊数值函数的刻划定理,并讨论了它们的相互关系.文献[3]讨论了模糊映射的一致凸性及其有关性质,给出了模糊映射为一致凸的几个判别准则,并得到了可微一致凸模糊映射在某一点达到最小值的充分条件.另外,在文献[4]所建立的拓扑向量空间及引进的序关系下,文献[5]引入了反模糊数的概念,建立了反模糊数空间,并讨论了有关基本性质,文献[6]提出了生成函数的概念,证明了由一类凸集生成的函数是模糊值凸函数,并利用上图的性质,建立了模糊值凸函数的下卷积、右乘等概念.
最近,模糊映射的共轭问题在模糊规划中越来越受重视.文献[7]给出了模糊值凸函数的共轭函数的概念,并给出了模糊值凸函数的共轭函数是模糊值凸函数等相关性质.而对于广义模糊凸函数,很多学者也做出了研究.比如,文献[8]在下半连续的条件下,给出了一个模糊集是预不变凸模糊集的充分条件,并将模糊凸集的相关性质在模糊不变凸集上作了相应的推广.文献[9]提出了新的半E-预不变凸模糊映射和拟半E-预不变凸模糊映射的概念,讨论了各类广义E-凸模糊映射之间的关系,并给出了这类新的广义凸模糊映射的一些性质及解集特征,得出了相应的最优性条件并将其应用在模糊规划中.
笔者受文献[4]所引入的序关系以及文献[10]中提出的m-凸函数的概念的启发,提出了一类模糊值m-凸函数的新概念.再结合文献[6-7,11-12]中关于对模糊凸函数的性质和共轭函数及下卷集研究的思想,讨论了模糊值m-凸函数基本性质和共轭问题,证明了其共轭映射在一定的条件下也是模糊值m-凸函数,并研究了模糊值m-凸函数的共轭函数与其下卷积之间的关系.
2 预备知识
实数集R上的一个模糊集u : R→[0,1]称为模糊数,如果u是正规的,凸的,上半连续的,且支集是紧集.用F0表示R上的所有模糊数构成的空间,称其为模糊数空间.
本文所讨论的模糊数值函数是指从n维欧氏空间Rn中的一个非空子集S到模糊数空间F0的映射,即f : S→F0.由模糊数的参数表达式,模糊数值函数表示为
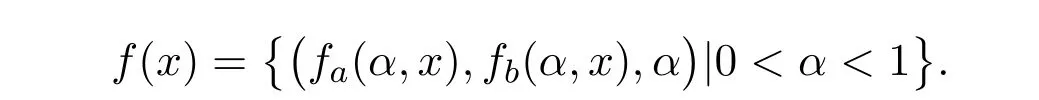
为了方便讨论,对于模糊数

记
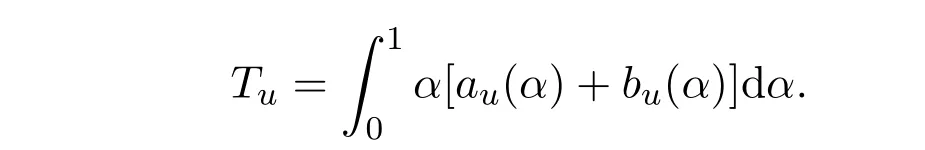
对于模糊数值函数
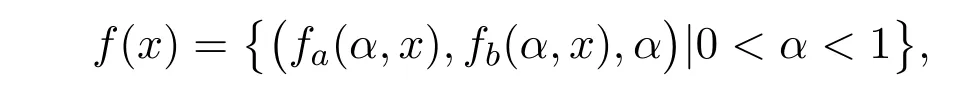
记
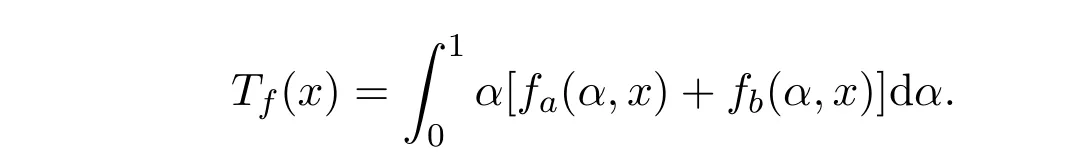
定义2.1[4]对于u ={(au(α),bu(α),α)|0<α<1}∈F0和
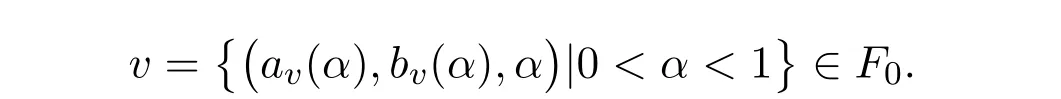
(1)如果Tu≤Tv,则称u≼v; (2)如果Tu= Tv,则称u = v;
对于u,v∈F0,λ>0,易证Tu+v= Tu+ Tv, Tλu=λTu.
定义2.2[12]设E是F0中的一个子集, M(m)∈F0称为E的上确界,如果M(m)满足下列条件:
(1)对任何u∈E,都有u≼M(m≼u),即M(m)为E的上(下)界;
(2)对E的每一个上界M0(m0),都有M≼M0(m0≼m).
定义2.3[10]函数f : [0,b]→R被称为m-凸函数,则对任意的x,y∈[0,b],λ∈[0,1]以及固定常数m∈(0,1],函数f满足
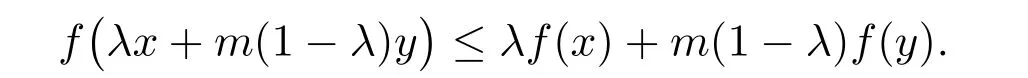
3 基本性质
结合定义2.3,下面给出m-凸集以及模糊值m-凸函数的概念.
定义3.1设y∈S⊆Rn,如果存在固定常数m∈(0,1],使得对任意x∈S,λ∈[0,1], 有λx+m(1−λ)y∈S,则称S关于y是m-凸的.若对任意的y∈S,有λx+m(1−λ)y∈S,则称S是一个m-凸集.
定义3.2设S为Rn中的非空m-凸集, m是(0,1]上的固定常数, f : S→F0为模糊值函数,如果对任意的x,y∈S,及λ∈[0,1],有

则称f为S上的模糊值m-凸函数.
由于模糊值m-凸函数f(x)可表示为{(fa(α,x),fb(α,x),α)|0<α<1},所以根据文献[5]中的定理1.7,易得fa(α,x)和fb(α,x)是m-凸函数.
定义3.3设E为Rn×F0中的一个非空子集,则称函数

为由E生成的模糊值函数,其定义域为

定理3.1设S是Rn上的m-凸集, f : S→F0是模糊值函数,则f是模糊值m-凸函数的充要条件是:∀x,y∈S,∀u,v∈F0及λ∈[0,1],当Tf(x)≤Tu, Tf(y)≤Tv时,有
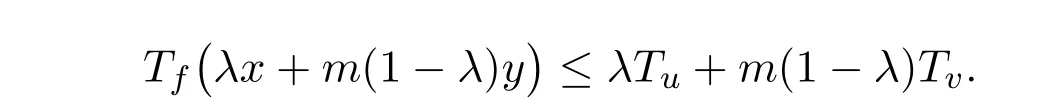
证明必要性.设f是凸模糊值m-凸函数,则有
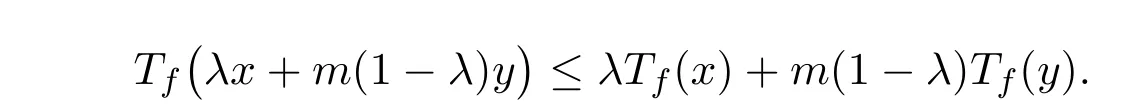
所以当Tf(x)≤Tu, Tf(y)≤Tv时,有
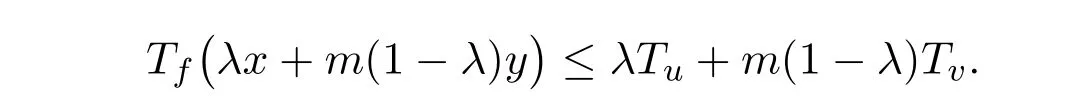
充分性.设x,y∈S,对任意的0<ε<1,取
有
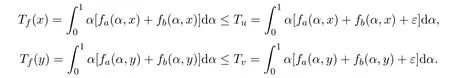
于是
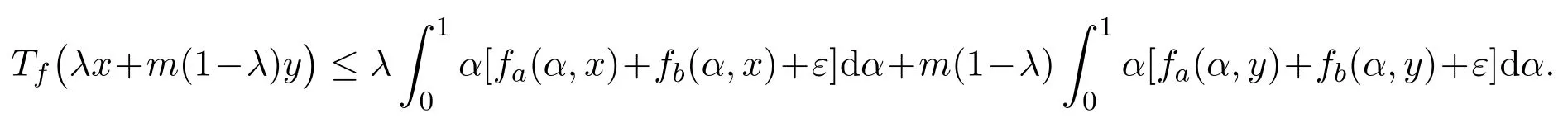
令ε→0+,可得
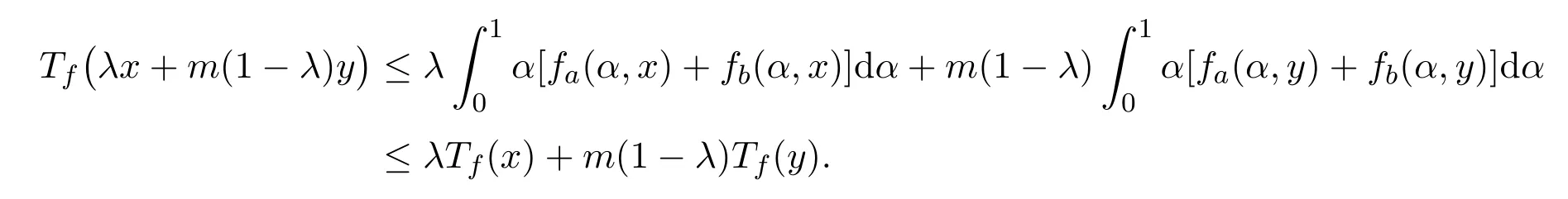
因此, f是凸模糊值m-凸函数.
下面给出关于模糊值m-凸函数f与其epi(f)的关系, epi(f)定义如下
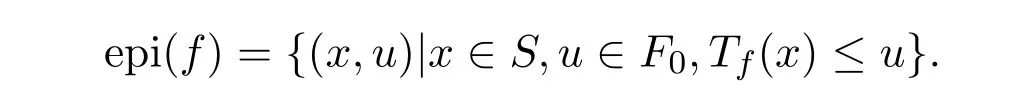
定理3.2设f : S→F0是模糊值函数,则f是模糊值m-凸函数的充要条件是epi(f) 是Rn×F0上的m-凸集.
证明充分性.设epi(f)是Rn×F0上的m-凸集,则对任意的
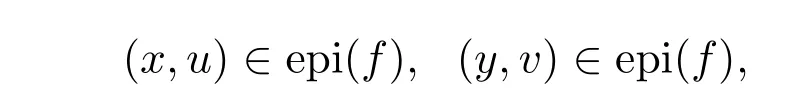
有Tf(x)≤Tu, Tf(y)≤Tv,且
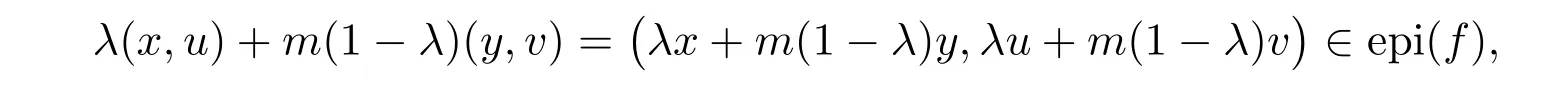
即
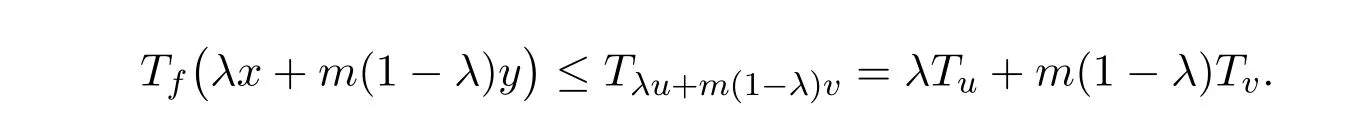
必要性.对任意的x,y∈S,有(x,f(x)),(y,f(y))∈epi(f).由于f是一个模糊值m-凸函数,则
所以
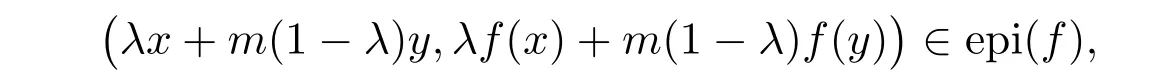
即epi(f)是Rn×F0上的m-凸集.
定理3.3设E为Rn×F0中的一个非空m-凸集,则由E生成的模糊值函数f是S = {x|存在u∈F0,使得(x,u)∈E,x∈Rn}上的模糊值m-凸函数,并且epi(f)⊂E.
证明对x,y∈S及λ∈[0,1],则有
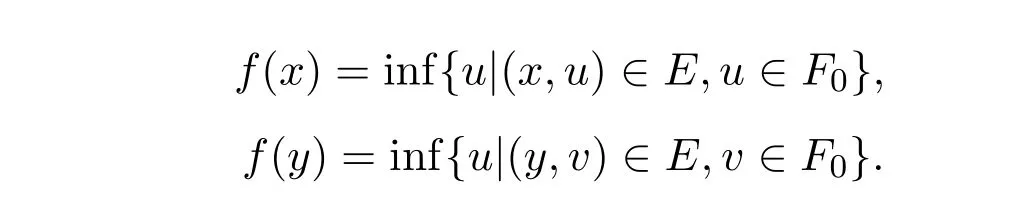
所以有f(x)≼u, f(y)≼v,即Tf(x)≤Tu, Tf(y)≤Tv.又由E的m-凸性,有
现场试验流程如图6所示,本次试验设计处理量为100 m3/d,水处理设备保持24 h稳定运行,累计试验20天。试验过程中,根据出水水质情况,每隔8~10 h对两级过滤器反洗一次。按照回注水指标要求,主要对处理流程进、出水油含量、悬浮物含量、粒径中值3个指标进行检测,水质检测方法及标准参照SY/T 5329-2012《碎屑岩油藏注水水质推荐指标》。
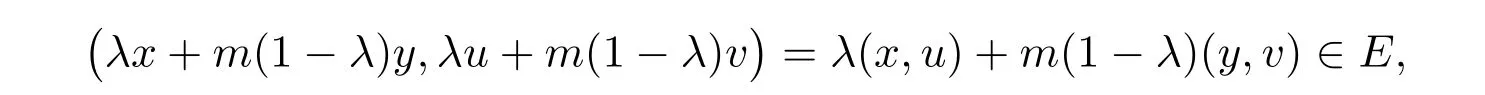
从而
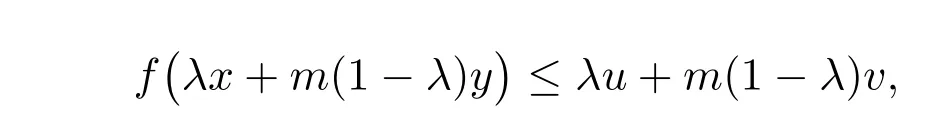
于是有
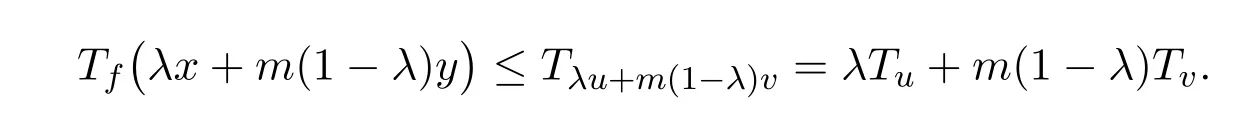
根据定理3.1,对任意的x,y∈S,当Tf(x)≤Tu, Tf(y)≤Tv时, f是S上的模糊值m-凸函数.
又由f(x) = inf{u|(x,u)∈E,u∈F0},则∀u∈{u|(x,u)∈E,u∈F0},有f(x)≼u, Tf(x)≤Tu,所以epi(f)⊂E.
定义3.4设f, g是m-凸集S上的两个模糊值m-凸函数,则称
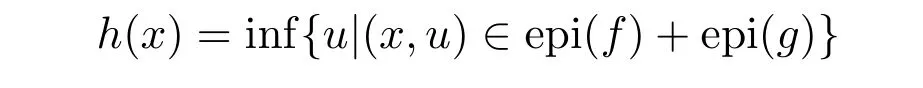
为f和g的下卷积,记为f⊗g.
由引理1.2[6]和定理3.3易推出f和g的下卷积f⊗g是S上的模糊值m-凸函数.
4 主要结果
定义4.1设f : S→F0为一个模糊值m-凸函数,令
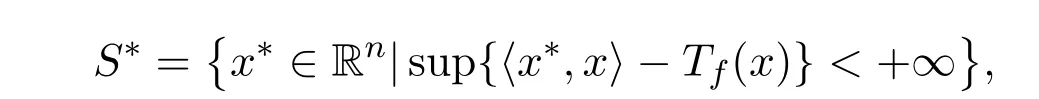
则称定义在S∗上的模糊值函数
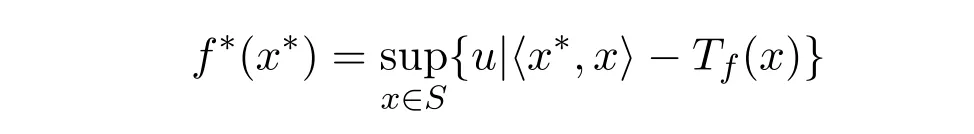
为f的共轭函数.
定理4.1模糊值m-凸函数f(x)在Tf(x)≥0情况下,其共轭函数f∗(x∗)也是模糊值m-凸函数.
证明设f : S→F0为一个模糊值m-凸函数,先证明
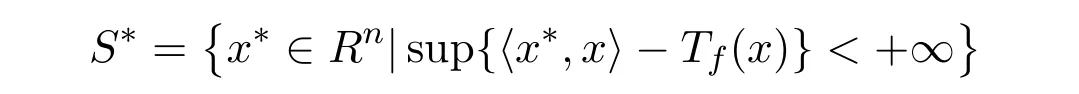
为m-凸集.任取a∗, b∗∈S∗则∀x∈S,有
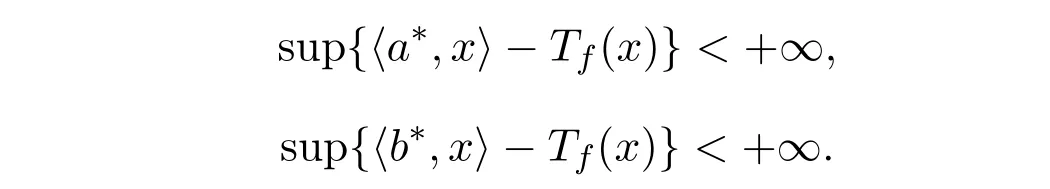
又∀λ∈[0,1],有
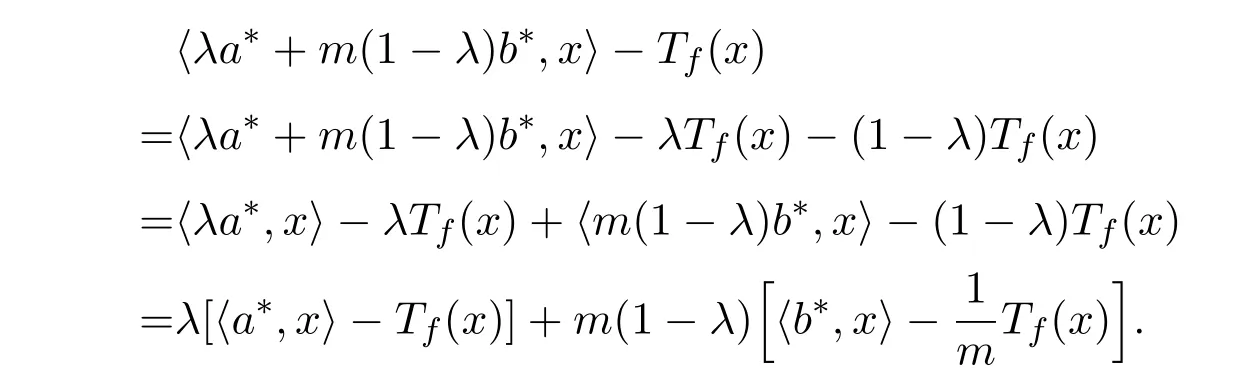
所以
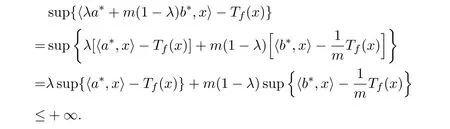
从而λa∗+ m(1−λ)b∗∈S∗,即S∗是一个m-凸集.下面证明f∗(x∗)是模糊值m-凸函数.任取x∗, y∗∈S∗,则有
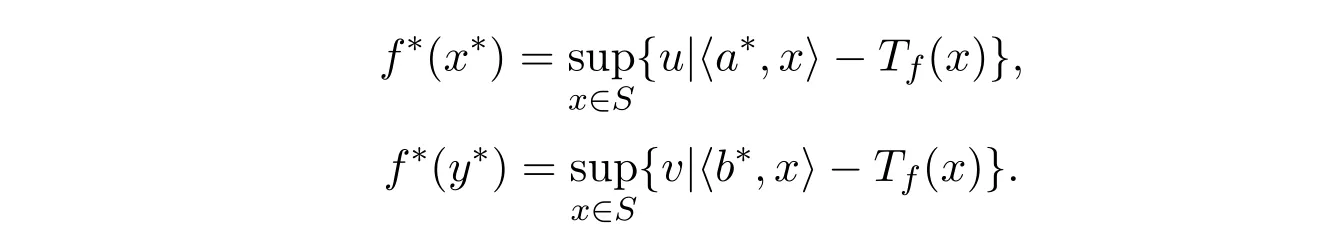
所以
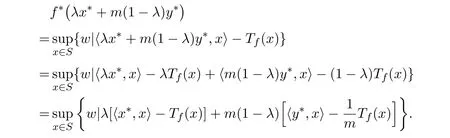
由于Tf(x)≥0,且m是(0,1]的固定常数,则
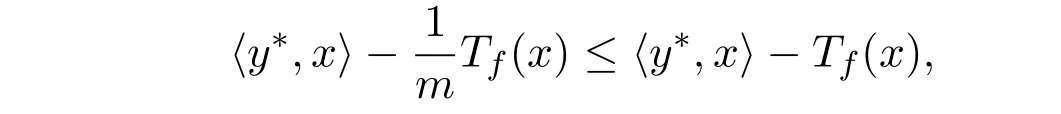
从而可得
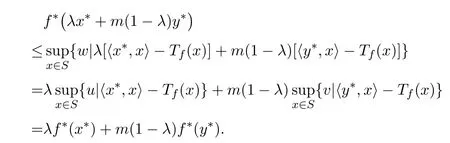
即
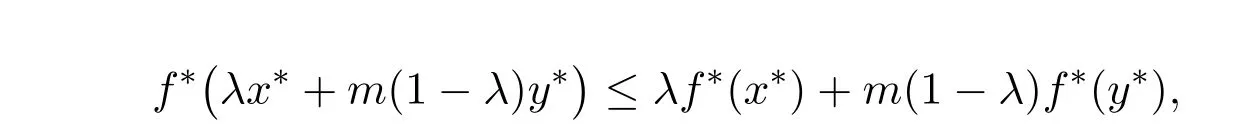
所以f∗是S∗上的模糊值m-凸函数.
定理4.2设f : S→F0和g : S→F0都是模糊值m-凸函数,则
(1)∀x∈S,若f(x)≼g(x),则f∗(x∗)≽g∗(x∗);
(2) (cf)∗(x∗) = cf∗(c−1x∗) (c>0).
证明(1)∀x∈S,若f(x)≼g(x),即Tf(x)≤Tg(x),所以对∀x∗∈S∗,有
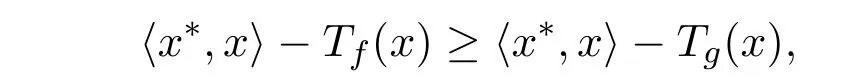
从而
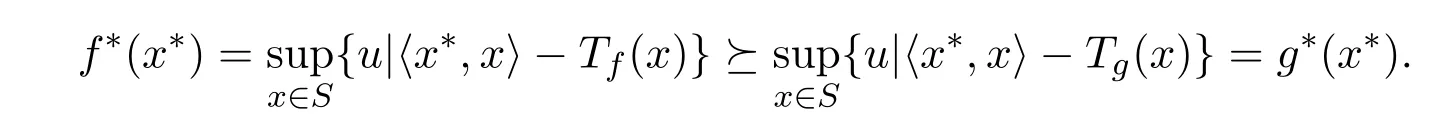
(2)当c>0时,则cf : S→F0也是一个模糊值m-凸函数.所以
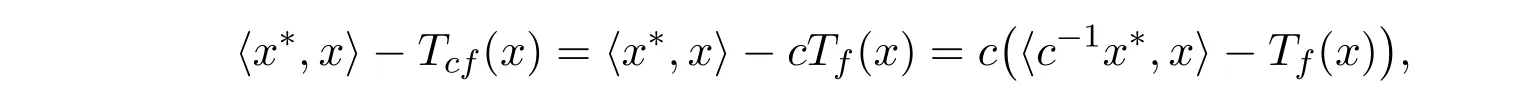
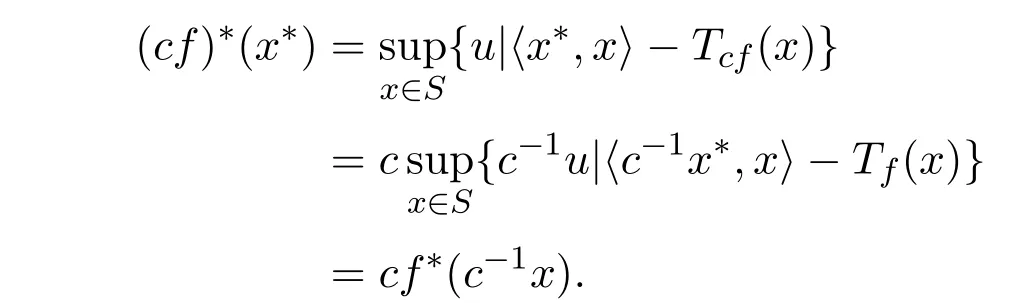
根据定理4.2的证明过程, f∗(x∗)和g∗(x∗)的大小关系与m无关,所以有如下推论.
推论4.1设f : S→F0和g : S→F0分别是模糊值m1-凸函数和模糊值m2-凸函数, ∀x∈S,若f(x)≼g(x),则f∗(x∗)≽g∗(x∗).
定理4.3设f : S→F0是模糊值m-凸函数, f∗(x∗)为f(x)的共扼映射.由f(x)可以表示为
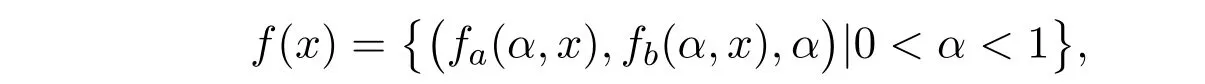
则
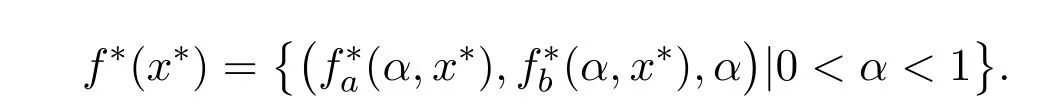
证明根据文献[5]中定理2.3的证明,又由于fa(α,x)和fb(α,x)是m-凸函数,所以f(x)的共扼映射可表示为
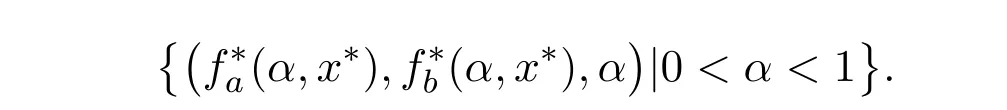
定理4.4设f,g : Rn→F0是两个模糊值m-凸函数, f∗,g∗分别为其共轭函数,则有
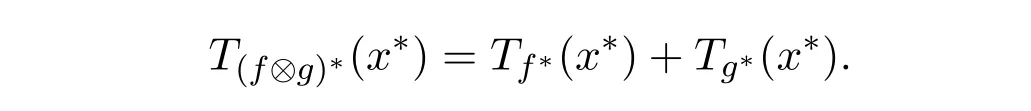
证明由于f和g的下卷积f⊗g也是模糊值m-凸函数,根据定理2.1[7],有
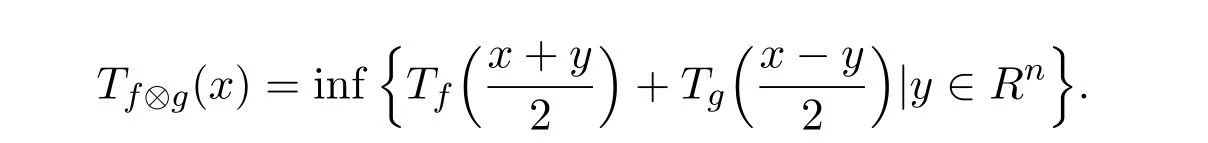
从而
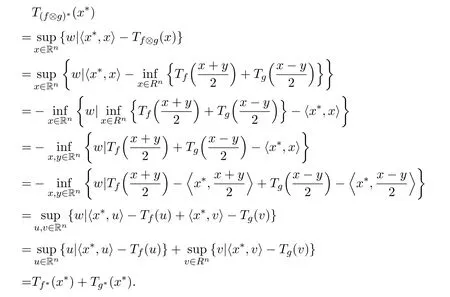
根据定理4.3,可以得出下面推论.
推论4.2设f,g : Rn→F0是分别是模糊值m1-凸函数和模糊值m2-凸函数, f∗,g∗分别为其共轭函数,则有
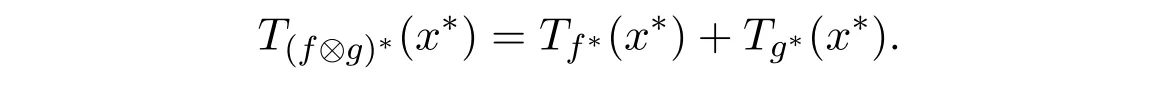
参考文献
[1] Chang S S L, Zadeh L A. On fuzzy mappings and control [J]. IEEE Trans. Syst. Man. Cybern., 1972,2:30-34.
[2]李红霞,巩增泰.模糊数值函数的凸性与可导性[J].西北师范大学学报, 2007,43(5):1-6.
[3]包玉娥,吴梅花.一致凸模糊映射及其有关性质[J].纯粹数学与应用数学, 2009,25(4):725-730.
[4] Goetschel-Voxman W. Elementary fuzzy calculus [J]. Fuzzy Sets and Systems, 1986,18:31-34.
[5]张成,袁学海.凸模糊映射的共轭映射[J].数学研究与评论, 2007,4:839-844.
[6]赵博,包玉娥,彭晓芹.一类模糊值凸函数的若干运算性质[J].模糊系统与数学, 2012,26(5):167-171.
[7]包玉娥,赵博,彭晓芹.关于模糊值凸函数的共轭问题的研究[J].纯粹数学与应用数学, 2013,29(4):331-337.
[8]张萍,黄虎,王早.预不变凸模糊集的一些性质[J].纯粹数学与应用数学, 2006,22(3):355-359.
[9]刘婷婷. E-凸模糊映射及其应用[D].重庆:重庆师范大学, 2014:18-27.
[10] Dragomir S S, Toader G H. Some inequalities for m-convex functions [J]. Studia Univ. Babes-Bolyai Math., 1993,38(1):21-28.
[11] Nanda S. On Fuzzy Integrals [J]. Fuzzy Sets and Systems, 1989,32:95-101.
[12] Yan Hong, Xu Jiuping. A class of convex fuzzy mappings [J]. Fuzzy Sets and Systems, 2002,129:47-56.
2010 MSC: 03E72
On characterization and conjugate problem involving fuzzy-valued m-convex functions
Liao Jiagen1, Du Tingsong1,2
(1. College of Science, China Three Gorges University, Yichang 443002, China 2. Hubei Province Key Laboratory of System Science in Metallurgical Process, Wuhan University of Science and Technology, Wuhan 430081, China)
Abstract:In this paper, we introduced a new class of generalized fuzzy-valued convex functions which called fuzzy-valued m-convex functions by modulating the m-convex functions. First, we studied some basic properties of the fuzzy-valued m-convex functions. Then we presented the conception of the conjugate function for fuzzyvalued m-convex functions and proved some related properties which the conjugate function of fuzzy-valued m-convex functions is also fuzzy-valued m-convex function under certain conditions. Finally we discuss the relationship between the conjugate functions and inf-convolution of two fuzzy-valued m-convex functions.
Key words:fuzzy-valued m-convex function, conjugate function, inf-convolution
通讯作者:杜廷松(1969-),硕士,教授,研究方向:凸分析及最优化理论与算法.
作者简介:廖甲根(1991-),硕士生,研究方向:凸性理论及其应用,模糊分析.
基金项目:国家自然科学基金(61374028);湖北省自然科学基金(2013CFA131);三峡大学培优基金(2015PY072).
收稿日期:2015-09-25.
DOI:10.3969/j.issn.1008-5513.2016.01.012
中图分类号:O159.2
文献标识码:A
文章编号:1008-5513(2016)01-0084-09

