具有线性微分算子的分数阶微分方程积分边值问题
李萌萌,贾梅,苏小凤
(上海理工大学理学院,上海 200093)
具有线性微分算子的分数阶微分方程积分边值问题
李萌萌,贾梅,苏小凤
(上海理工大学理学院,上海200093)
摘要:研究一类具有分数阶线性微分算子的非线性微分方程积分边值问题解的存在性与唯一性.利用Schauder不动点定理及压缩映射原理,建立并证明了边值问题解的存在性定理和唯一性定理,并给出两个例子以说明所得结论.
关键词:分数阶线性微分算子;积分边值问题; Riemann-Liouville分数阶导数;不动点定理
1 引言
由于分数阶微积分在科学研究和工程技术等领域具有广泛的应用,近年来分数阶微分方程的理论研究取得了一系列研究成果[1-4].边值问题是微分方程理论研究的重要课题,许多学者对分数阶微分方程边值问题解的存在性与唯一性进行了大量研究[512].在对具有Riemann-Liouville导数分数阶微分方程边值问题的研究中,较多是假设未知函数在左端点的值为零, 即x(0) = 0的情况,例如参考文献[7-10].本文在文献[7]基础上,在不假设x(0) = 0情况下,利用Schauder不动点定理和压缩映射原理,研究了如下一类具有分数阶线性微分算子的非线性微分方程积分边值问题:

的解的存在性及唯一性,其中
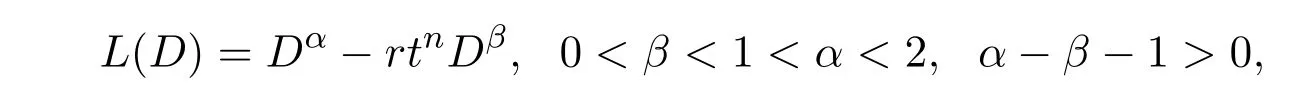
n为非负整数, r∈R, Dα和Dβ均为标准的Riemann-Liouville分数阶导数, f : [0,1]×R→R满足L1-Carathe´odory条件, gi∈C[0,1], i = 1,2.
函数f : [0,1]×R→R称为满足L1-Carathe´odory条件,如果
(1)对任意的x∈R,函数f(·,x) : [0,1]→R是可测的;
(2)对几乎处处的t∈[0,1],函数f(t,·) : R→R是连续的;
(3)对任意γ>0,存在ϕγ∈L1[0,1],使得当|x|≤γ时,对几乎处处t∈[0,1] 有|f(t,tα−2x)|≤ϕγ(t).
2 预备知识
有关Riemann-Liouville分数阶导数和积分定义可参见参考文献[1-2].
引理2.1[2]设α>0, 0≤γ<1,γ≤α,则分数阶积分算子Iα: C0γ[0,1]→C[0,1].
引理2.2[5]若α>0, 0<β<1,β≤α, I1−βx(t)|t=0= 0, n为非负整数,则
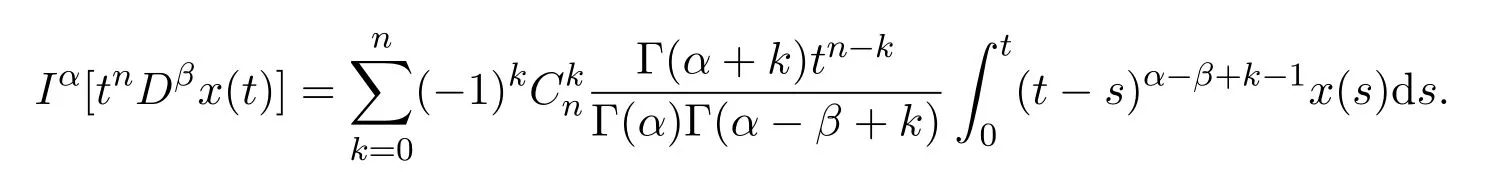
引理2.3对任意的h∈L1[0,1],边值问题
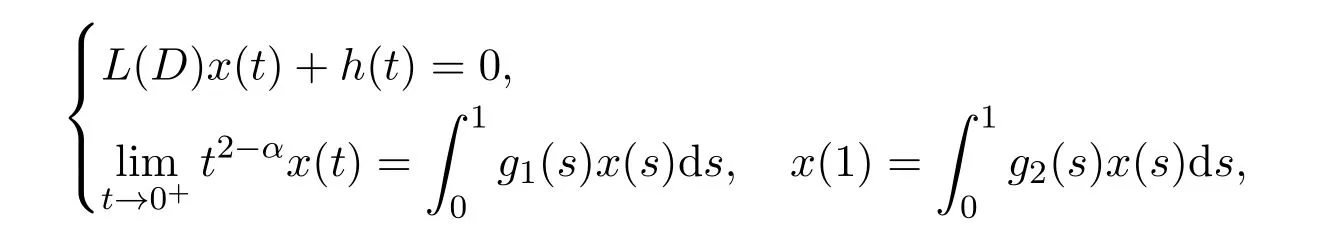
在X中等价于下面的积分方程:
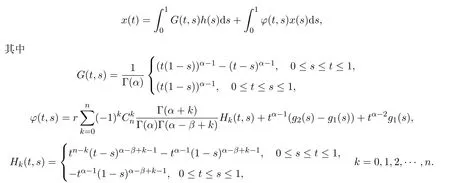
证明因为α−β−1>0,所以根据引理2.1可得,对任意x∈X, I1−βx(t)|t=0= 0.
由引理2.2可以得到
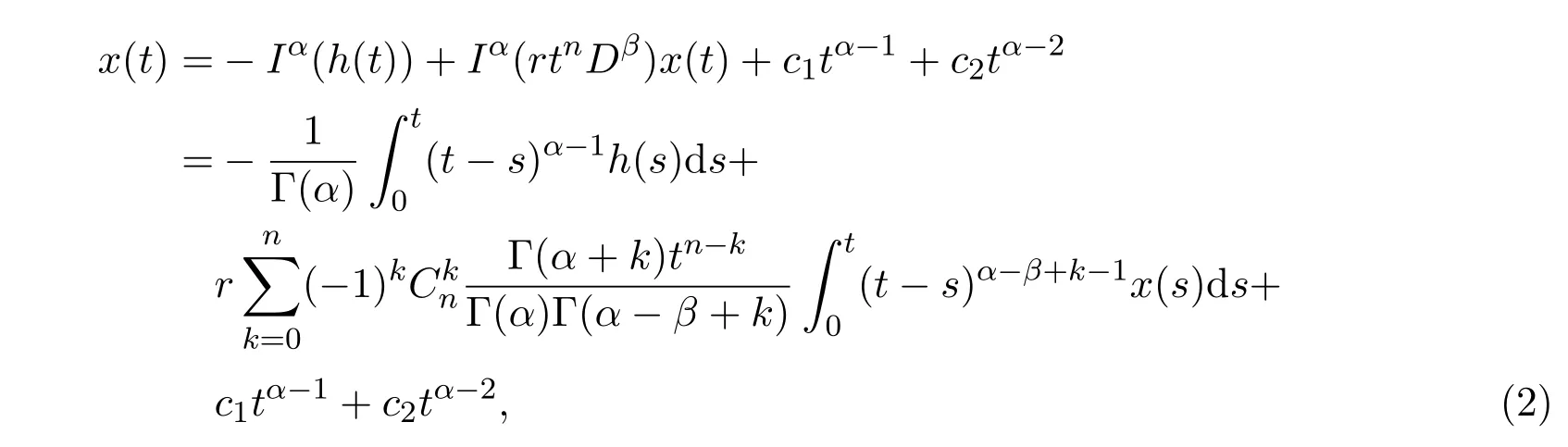
其中c1,c2∈R.将边界条件代入上式,解之得

因此,将c1和c2代入(2)式,可得
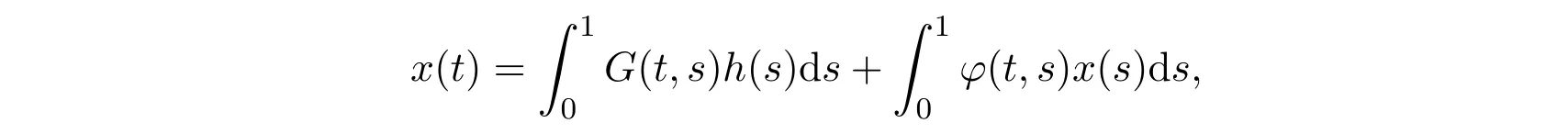
其中G(t,s), Hk(t,s),φ(t,s)即为上面形式.
由引理2.3、函数G(t,s)和Hk(t,s),k = 0,1,2,···,n的表达式易得下面引理2.4、引理2.5和引理2.6.
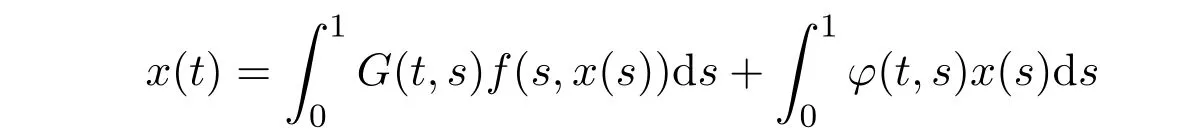
的解.
引理2.5函数G(t,s)满足:
(1) G(t,s)∈C([0,1]×[0,1]),且对于任意t,s∈(0,1)有G(t,s)>0;
(2)当t,s∈[0,1]时,
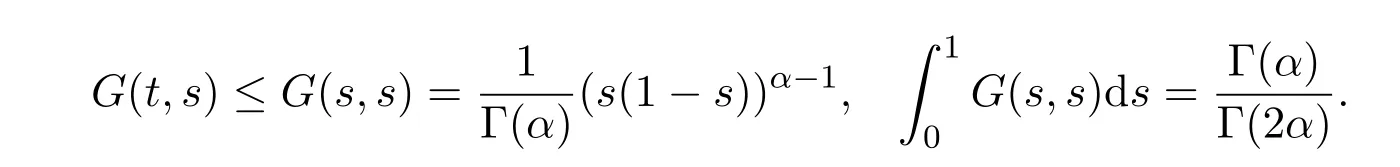
引理2.6对k = 0,1,2,···,n,函数Hk(t,s)满足:
(1) Hk(t,s)∈C([0,1]×[0,1]);
(2)对于任意的t,s∈[0,1],有|Hk(t,s)|≤tα−1(1−s)α−β+k−1.
定义算子T : X→X,
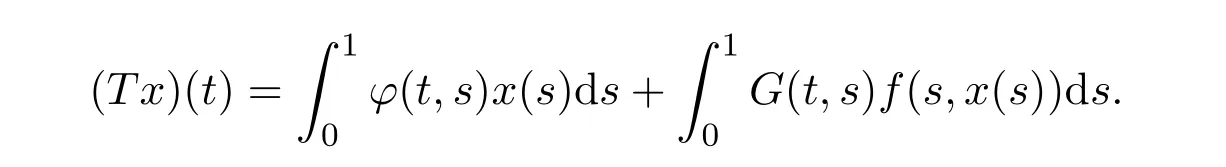
引理2.7算子T : X→X是全连续的.
证明设{xn}⊂X, x∈X,满足当n→∞时, ||xn−x||→0,故存在γ1>0,使得||xn||≤γ1, ||x||≤γ1,即对任意的t∈[0,1], |t2−αxn(t)|≤γ1, |t2−αx(t)|≤γ1,因此对几乎处处s∈[0,1],有
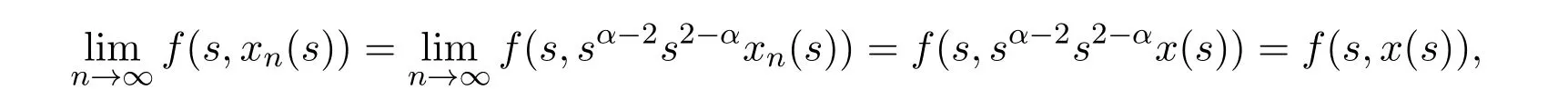
并且存在ϕγ1∈L1[0,1],当s∈[0,1]时, |f(s,xn(s))| = |f(s,sα−2s2−αxn(s))|≤ϕγ1(s).
由Lebesgue控制收敛定理得
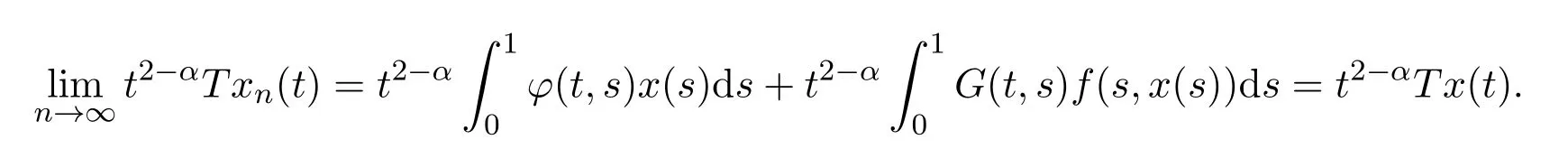
所以, ||Txn−Tx||→0, (n→∞),故T : X→X是连续算子.
设Ω⊂X是任意一个有界集,则存在γ2>0,使得当x∈Ω时,有||x||≤γ2,即存在ϕγ2∈L1[0,1],对任意的x∈Ω,有

所以T(Ω)是一致有界的.
另外,对任意的x∈Ω,因为Hk(t,s)∈C([0,1]×[0,1]), gi∈C[0,1], i = 1,2,所以t2−αφ(t,s)∈C([0,1]×[0,1]),故t2−αφ(t,s)一致连续.又G(t,s)∈C([0,1]×[0,1]),故G(t,s)一致连续.因此易得对任意的ε>0,存在δ>0,对任意的t1,t2∈[0,1],当|t1−t2|<δ时,有所以T(Ω)是等度连续的,由Arzela-Ascoli定理知, T : X→X是相对紧的.
综上可得T : X→X是全连续的.
3 解的存在性及唯一性
记
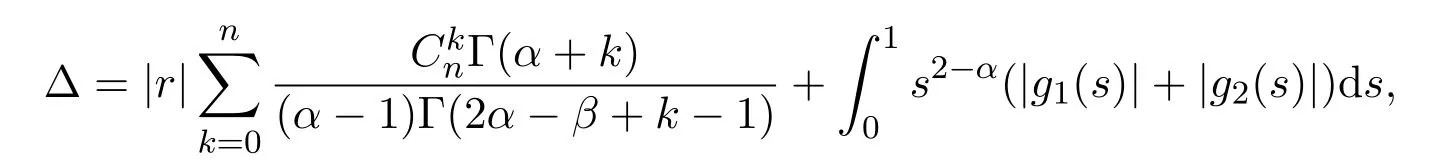
则有∆≥0.
假设: (H) 0≤∆<1.
(H1)存在非负函数p(t)∈L1[0,1], q(x)在R上连续,使得|f(t,x)|≤p(t) + q(x),且
(H2)存在非负函数t2α−3a(t)∈L1[0,1], b(t)∈L1[0,1],常数σ>0,使得对任意的t∈[0,1] 及x∈R,有|f(t,x)|≤a(t)|x|σ+ b(t).
(H3)存在函数l(t)>0, t2α−3l(t)∈L1[0,1],使得当t∈[0,1], x1,x2∈R时,

定理3.1假设条件(H), (H1)成立,且A = 0,则边值问题(1)在X中至少存在一个解.
证明取

由(H1)知,存在d1>0,使得当|x|>d1时,
取
则D为X中非空有界闭凸集.
对任意的x∈D,有||x||≤d0.因此当t∈(0,1]时,

故

所以T : D→D.
又由引理2.7知T全连续,故由Schauder不动点定理, T在D中至少存在一个不动点,即边值问题(1)在X中至少存在一个解.
由(H1)知,存在d1>0,使得当|x|≥d1时, 0≤q(x)≤(A+ε)|x|.令对任意的x∈R,有0≤q(x)≤N + (A +ε)|x|.
取

令D = {x|x∈X,||x||≤d0},则D为X中非空有界闭凸集.
与定理3.1证明类似可证||Tx||≤d0,所以T : D→D.
又由引理2.7知T全连续,故由Schauder不动点定理, T在D中至少存在一个不动点,即边值问题(1)在X中至少存在一个解.
定理3.3假设条件(H), (H2)成立,且0<σ<1,则边值问题(1)在X中至少存在一个解.

选取

令D = {x|x∈X,||x||≤r1},则D为X中非空有界闭凸集.∀x∈D,有与定理3.1证明类似可证||Tx||≤r1,即T(D)⊂D.又由引理2.7知T全连续,故由Schauder不动点定理, T在D中至少存在一个不动点,即边值问题(1)在X中至少存在一个解.
定理3.4假设条件(H), (H2)成立,且
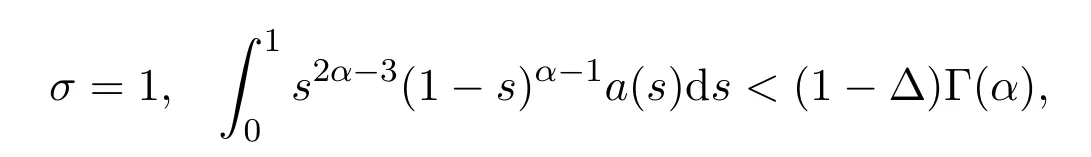
则边值问题(1)在X中至少存在一个解.
证明取
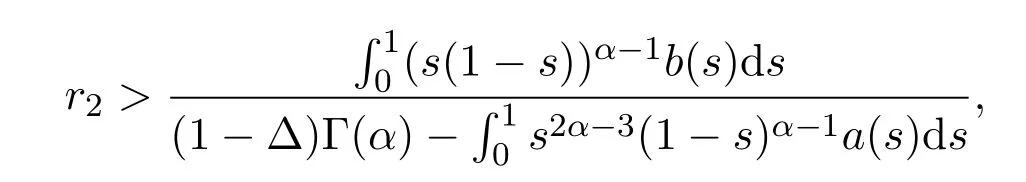
则有r2>0.
令D = {x|x∈X,||x||≤r2},则D为X中非空有界闭凸集.对任意的x∈D,易得||Tx||≤r2,即T(D)⊂D.又由引理2.7知T全连续,故由Schauder不动点定理, T在D中至少存在一个不动点,即边值问题(1)在X中至少存在一个解.
定理3.5假设条件(H3)成立,且

则边值问题(1)在X中存在唯一的解.
证明对任意的x,y∈X, t∈[0,1],

所以,
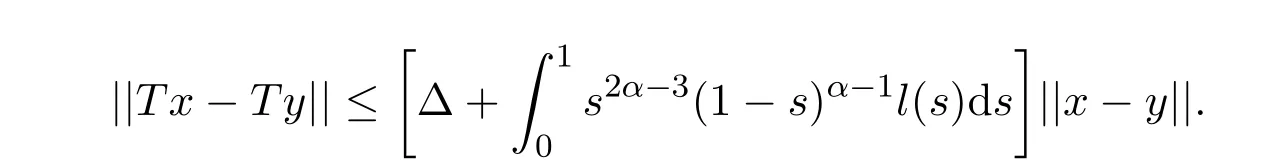
由于

故T : X→X是压缩映射,利用压缩映射原理可得, T在X中有唯一不动点,即边值问题(1) 在X中存在唯一的解.
4 应用举例
例4.1考虑边值问题

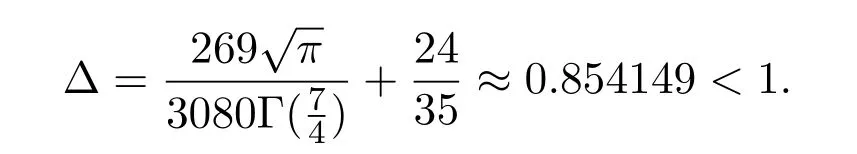
例4.2考虑边值问题

其中
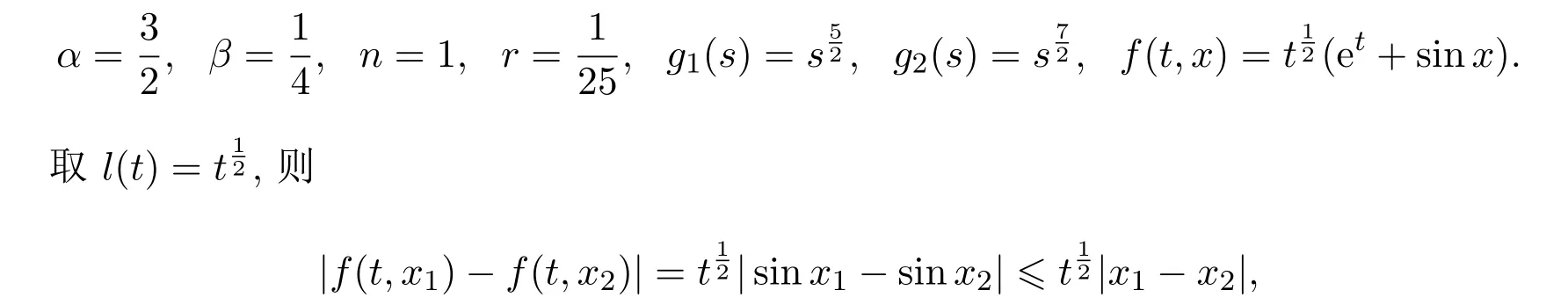
且
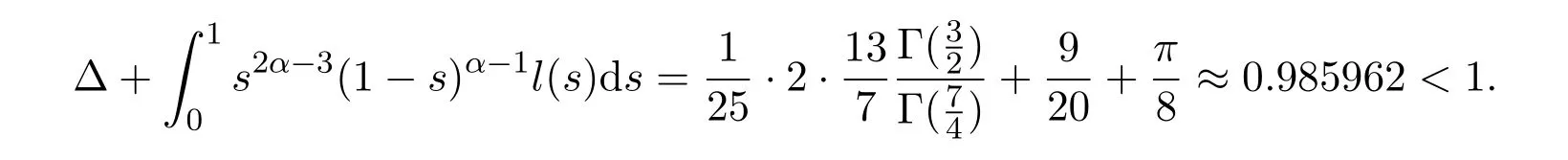
故由定理3.5可得,边值问题(4)存在唯一解.
参考文献
[1] Podlubny I. Fractional Differential Equations [M]. New York: Academic Press, 1999.
[2] Kilbas A A, Srivastava H M, Trujillo J J. Theory and Applications of Fractional Differential Equations [M]. Amsterdam: Elsevier Science Ltd, 2006.
[3] Miller K S, Ross B. An Introduction to the Fractional Calculus and Fractional Differential Equations [M]. New York: Wiley, 1993.
[4]白占兵.分数阶微分方程边值问题理论及应用[M].北京:中国科学技术出版社, 2012.
[5] Babakhani A. Existence and uniqueness of solution for class of fractional order differential equations on an unbounded domain [J]. Advances in Difference Equations, 2012,2012,41:1-8.
[6]刘帅,贾梅,秦小娜,等.带积分边值条件的分数阶微分方程解的存在性和唯一性[J].上海理工大学学报, 2014,36(5):409-415.
[7]吴贵云,刘锡平,杨浩.具有微分算子的分数阶微分方程边值问题解的存在性与唯一性[J].上海理工大学学报, 2015,37(3):205-209.
[8] Liu Xiping, Wu Guiyun. Existence of positive solutions for integral boundary value problem of fractional differential equations [J]. Journal of Shanghai Normal University, 2014,43(5):496-505.
[9] Jiang Daqing, Yuan Chengjun. The positive properties of the Green function for Dirichlet-type boundary value problems of nonlinear fractional differential equations and its application [J]. Nonlinear Analysis, 2010,72(2):710-719.
[10] Cabada A, Hamdi Z. Nonlinear fractional differential equations with integral boundary value conditions [J]. Applied Mathematics and Computation, 2014,228(1):251-257.
[11]张海斌,贾梅,陈强.一类半无穷区间上分数阶非线性微分方程边值问题多个正解的存在性[J].吉林大学学报(理学版), 2014,52(6):1145-1150.
[12]桂旺生,刘利斌.分数阶微分方程m点边值共振问题解的存在性[J].纯粹数学与应用数学, 2015,31(1):1-11.
2010 MSC: 34B15, 26A33
The integral boundary value problem for fractional differential equations with linear differential operator
Li Mengmeng , Jia Mei , Su xiaofeng
(College of Science, University of Shanghai for Science and Technology, Shanghai 200093, China)
Abstract:In this paper, we study the existence and uniqueness of solutions for a class of integral boundary value problem of differential equation with fractional linear differential operator. By using Schauder fixed point theorem and Banach contraction principle, the theorems of the existence and the uniqueness of solutions for the boundary value problem are obtained and proved. And we give two examples to illustrate the results.
Key words:fractional linear differential operator, integral boundary value problem, Riemann-Liouville fractional derivative,fixed point theorem
通讯作者:贾梅(1963-),硕士,副教授,研究方向:常微分方程理论与应用.
作者简介:李萌萌(1990-),硕士生,研究方向:常微分方程理论与应用.
基金项目:国家自然科学基金(11171220);沪江基金(B14005).
收稿日期:2015-08-31.
DOI:10.3969/j.issn.1008-5513.2016.01.011
中图分类号:0175.8
文献标识码:A
文章编号:1008-5513(2016)01-0075-09

