关于预可解子范畴的同调维数

郭娇霞,杨晓燕

(西北师范大学数学与统计学院,甘肃兰州　730070)



关于预可解子范畴的同调维数

郭娇霞,杨晓燕

(西北师范大学数学与统计学院,甘肃兰州730070)

摘要：引入了关于阿贝尔范畴中预可解子范畴的同调维数,讨论了这些同调维数的一些性质.并进一步给出了R模范畴中的X-Gorenstein投射维数和X-Gorenstein内射维数的定义及运用.

关键词：预可解子范畴;同调维数;生成子

1　引言

在古典同调理论中,同调维数是重要且基础的不变量,并且一些确定的模的子范畴都定义了相关的模的同调维数.例如:模的平坦、内射范畴都分别定义了相关的平坦、内射维数.当平坦模,内射模推广到Gorenstein平坦模和Gorenstein内射模时,又有了对应的Gorenstein同调维数理论[1-6].文献[7]研究了同一范畴的不同子范畴所定义的同调维数之间的关系及一些性质.受到这些工作的启发,本文继续研究了这些维数的一些性质.

第二部分,引入了阿贝尔范畴中的预可解子范畴的同调维数,给出了这些同调维数的一些性质.第三部分,讨论了R模范畴中的X-Gorenstein投射维数和X-Gorenstein内射维数.

本文中, A是一个阿贝尔范畴并且A的所有子范畴都是满的加法子范畴.

下面首先回顾一些基本的定义.

定义1.1[7]设C为A的子范畴且n≥0.

(1)若存在A中的正合列

其中Ci∈C,则M叫作A的一个n-C-合冲, A叫作M的一个n-C-余合冲.

(2)对A∈A, A的C维数定义为:

记作C-dim A.若不存在整数n,则记C-dim A =∞.

定义1.2设C为A的子范畴.记

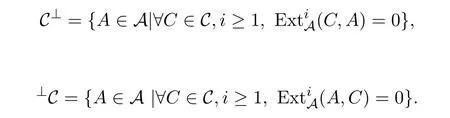
定义1.3[2]设E为A的子范畴. A中的一个序列S :···→S1→S2→S3→···叫作HomA(E,-)-正合的,如果对于任意的E∈E, HomA(E,S)是正合的. A中的满同态f叫作E-真的,如果它是HomA(E,-)-正合的.

定义1.4[6]设C,T都为A的子范畴,且C⊆T .

(1) C叫作T的生成子,若对任意的T∈T ,存在正合列0→T′→C→T→0,其中C∈C; C叫作T的余生成子,若对任意的T∈T ,存在正合列0→T→C→T′→0,其中C∈C.

(2)设E为A的子范畴. C叫作T的一个E-真生成子,若对任意的T∈T ,存在一个HomA(E,-)-正合的正合列0→T′→C→T→0 ,使得C∈C, T′∈T .

定义1.5[9]设E和T为A的子范畴. T叫作A中的E-预可解子范畴,若满足以下条件:

(1) T有一个E-真生成子.

(2) T关于E-真扩张封闭,也就是说,对任意的HomA(E,-)-正合的正合列

若A1,A3∈T ,则A2∈T .

A的一个E-预可解子范畴T叫作E-可解子范畴,若T满足以下条件.

(3) T关于E-真满同态的核封闭,即对任意的HomA(E,-)-正合的正合列

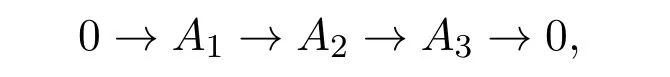
若A2,A3∈T ,则A1∈T .

对偶的,可定义C-余维数, E-预余可解子范畴, E-余真余生成子.

引理1.6设C,T都为A的子范畴, C为T的生成子且C关于直和项封闭.则T∩⊥T⊆C.

2　相对于预可解子范畴的同调维数

在此部分中, E和T都为A的子范畴.

引理2.1设C为A的关于扩张封闭的子范畴.考虑A中的正合列

其中T1,T0∈T .

(1)若T为A的E-预余可解子范畴,且C为T的E-余真余生成子,则存在HomA(E,-)-正合的正合列

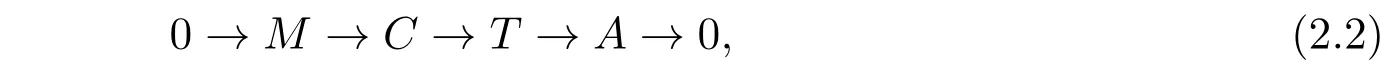
其中T∈T , C∈C.

(2)若T为A的E-预可解子范畴,且C为T的E-真生成子,则存在HomA(E,-)-正合的正合列

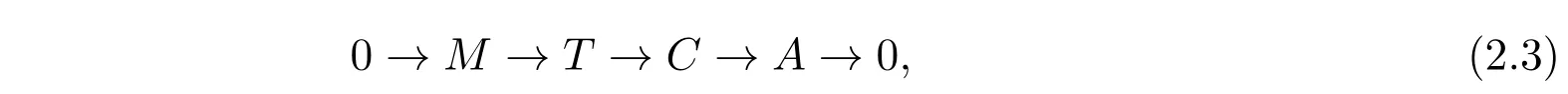
其中T∈T , C∈C.

证明(1)由条件存在正合列

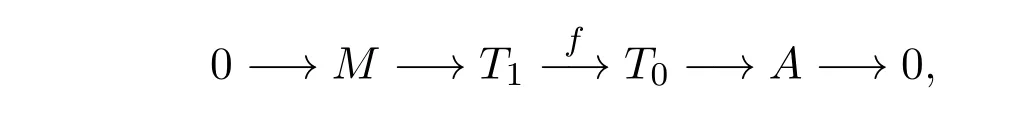
其中T1,T0∈T .因为C为T的余真余生成子,所以存在一个HomA(-,E)-正合的正合列0→T1→C→T′1→0,其中C∈C, T′1∈T .则有以下推出图,如图1所示:

图1　推出图

考虑以下推出图,如图2所示:

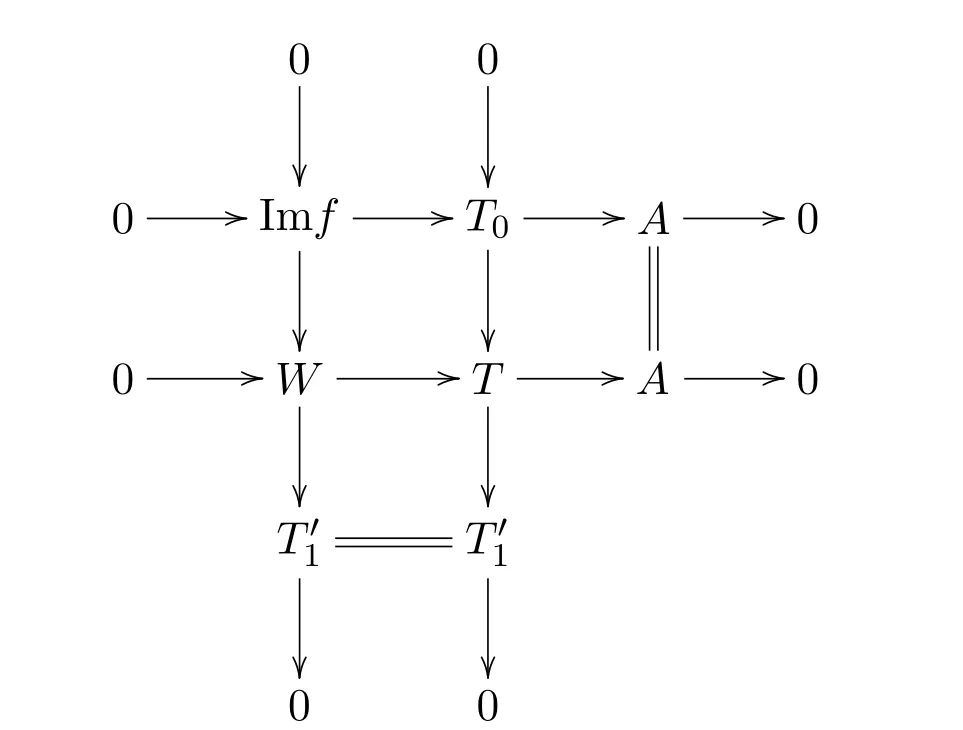
图2　推出图

因为图1中的第二列是HomA(E,-)-正合的,所以由文献[7]中的引理2.4(1),可知图1中的第三列(图2中的第一列)及图2的第二列也是HomA(E,-)-正合的.又因为T0,T′1∈T ,所以T∈T .连接两图的中间行即为所要的(2.2)式.

(2)对偶于以上证明当C为T的真生成子

引理2.2设n≥1.考虑A中的以下正合列

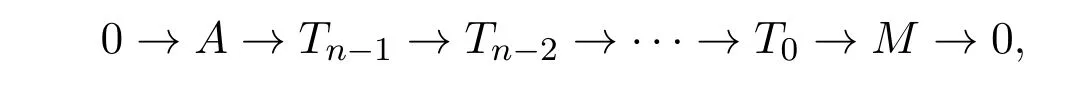
其中Ti∈T .

(1)若T为A的E-预余可解子范畴, C为T的E-余真余生成子,则存在正合列

及HomA(E,-)-正合的正合列0→M→N→T→0,其中Ci∈C,T∈T .

(2)若T为A的E-预可解子范畴, C为T的E-真生成子,则存在正合列

及HomA(E,-)-正合的正合列0→T→B→A→0,其中Ci∈C,T∈T .

证明(1)用数学归纳法.当n = 2时,由引理2.1已证.现假设n≥3.考虑正合列

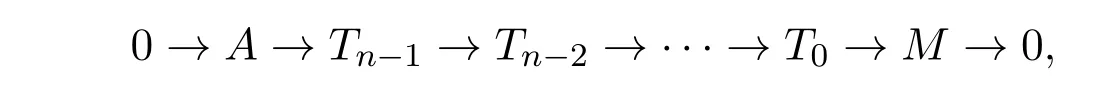
其中Ti∈T .令K = Ker(Tn−3→Tn−4),则由引理2.1知存在正合列

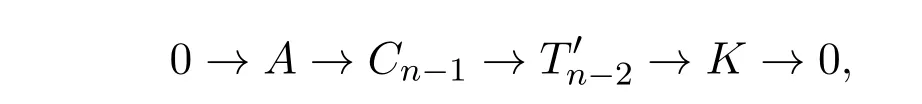
其中Cn−1∈C, T′n−2∈T .令A′= Im(Cn−1→T′n−2),由归纳假设存在正合列

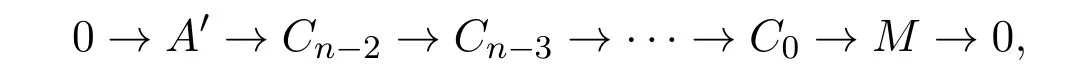
其中Ci∈C.因此得到正合列

其中Ci∈C.

(2)对偶于(1)可得证.

定理2.1设A∈A且n≥1, C为T的E-真生成子与E-余真余生成子.则下列条件等价:

(1) T -dimA≤n.

(2)存在一个正合列

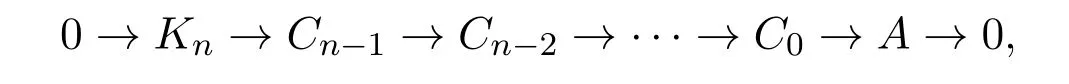
其中Ci∈C,Kn∈T .

(3)对任意非负整数t存在一个正合列

使得Xt∈T ,且对i = 0,···,t−1,t + 1,···,n,Xi∈C.

证明(2)⇒(1),(3)⇒(1),(3)⇒(2)显然. (1)⇒(2)由[9]中的引理3.6已证.

(1)⇒(3)用数学归纳法.当n = 1时存在正合列0→T1→T0→A→0,其中T1,T0∈T .则由引理2.1知,存在正合列0→C1→T′0→A→0及0→T′1→C0→A→0,其中现假设n≥2.则存在正合列

其中Ti∈T ,0≤i≤n.令Q = Ker(T1→T0).则有正合列

于是由引理2.1得正合列0→Q→T′1→C0→A→0.故有正合列

其中T′1∈T ,C0∈C.令N = Ker(C0→A),可知T -dimN≤n−1.则由归纳假设,存在正合列

其中Xt∈T ,Xi∈C,C0∈C,i /= t.

3　 X-Gorenstein投射模和X-Gorenstein内射模

在本节中, R是一个环并且R模范畴中的所有子范畴都是满的加法子范畴.对于R模范畴中的模A,用pdRA,idRA,fdRA分别表示A的投射维数,内射维数,平坦维数. P,I分别表示由投射模和内射模组成的范畴.

设X是一个包含投射模的模类, A为一个R-模. A叫作X-Gorenstein投射的,若存在一个HomR(-,X)-正合的正合列

其中每个层次都为投射的,使得A～= Im(P0→P0).记X-GP为R-模的由X-Gorenstein投射模组成的子范畴. A的X-Gorenstein投射维数定义为:

若不存在整数n,则记X-GpdRA =∞.

命题3.1设A为一个R-模.

(1)若A∈(X-GP)⊥,则pdRA = X-GpdRA.

(2)若pdRA＜∞,则pdRA = X-GpdRA = (⊥P)-dimA.

(3)若X-GpdRA＜∞,则X-GpdRA = (⊥P)-dimA.

(4)若fdRA＜∞,则pdRA = X-GpdRA.

证明(1)显然P是X-GP的P-真生成子与P-余真余生成子.由文献[7]中的引理3.1知X-GP关于扩张封闭.再由文献[9]中的引理3.10(3),令

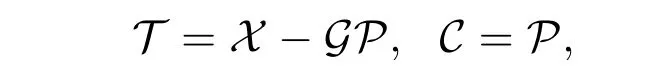
则对A∈(X-GP)⊥,有pdRA = X-GpdRA.

(2)由文献[9]中的命题5.3(1),有pdRA = (⊥P)-dimA,若pdRA＜∞.

(3)已知X-GP关于扩张封闭.设X-GpdRA = n＜∞.则由定理2.1存在一个正合列

其中Pi∈投射模, Gi∈X-GP.对于任意的1≤i≤n−1,令Ki= Im(Pi→Pi−1).假设

显然m≥n.事实上若m＜n,则由文献[9]中的定理3.8(1)知Km∈⊥P,Kn−1∈⊥P.因为存在一个HomR(-,X)-正合的正合列0→Gn→P→G→0,其中P∈投射模, G∈X-GP,

有以下推出图,如图3所示:

图3　推出图

因为图3中的中间行和中间列都是可裂的,所以G′～= Pn−1⊕G∈X-GP,且Kn−1同构于G′的直和项,这表明Kn−1∈X-GP,且X-GpdRA≤n−1.矛盾.

(4)由X-Gorenstein投射模的定义,很容易看到A∈(X-GP)⊥.类似于(1)的证明即可.

设X是一个包含内射模的模类, A为一个R-模. A叫作X-Gorenstein内射的,若存在一个HomR(X,-)-正合的正合列···→I1→I0→I0→I1→···其中每个层次都为内射的,使得A～= Im(I0→I0).记X-GI为R-模的由X-Gorenstein内射模组成的子范畴. A的X-Gorenstein内射维数定义为:

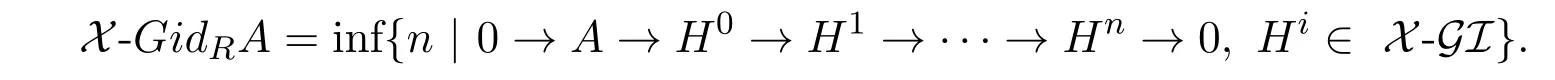
若不存在整数n,则记X-GidRA =∞.

对偶于命题3.1,有以下结论.

命题3.2设A为一个R-模.

(1)若A∈⊥(X-GI),则idRA = X-GidRA.

(2)若idRA＜∞,则idRA = X-GidRA = (I⊥)-codimA.

(3)若X-GidRA＜∞,则X-GidRA = (I⊥)-codimA.

参考文献

[1] Auslander M, Bridger M. Stable Module Theory [M]. American Mathematical Society: Providence Rbode Island, 1969.

[2] Enochs E E, Jenda O M G. Relative Homological Algebra [M]. De Gruyter Expositions in Mathematics. Berlin: Walter de Gruyter, 2000.

[3] Enochs E E, Jenda O M G. Gorenstein injective and projictive module [J]. Math. Z., 1995,220:611-633.

[4] Christensen L W. Gorenstein Dimension [M]. Lect. Notes in Math. 1747. Berlin: Springer-Verlag, 2000.

[5] Christensen L W, Iyengar S. Gorenstein dimension of module over homomorphism [J]. J. pure Appl. Algebra, 2009,208:177-188.

[6] Sather-Wagstaff S, Sharif T, White D. Stablity of Gorenstein categories [J]. J. Lond. Math. Soc., 2008,7:491-606.

[7] Huang Z Y. Proper resolutions and Gorenstein categories [J]. J. Algebra, 2009,393:142-169.

[8] Holm H. Gorenstein homological dimensions [J]. J. pure Appl. Algebra, 2004,189(1):167-193.

[9] Huang Z Y. Homological dimensions relative to preresolving subcategories [J]. Kyoto J. Math., 2014,54:727.

2010 MSC: 16D40

Homological dimensions with respect to preresolving subcategories

Guo Jiaoxia , Yang Xiaoyan
(Department of Mathematics , Northwest Normal University, Lanzhou 730070, China)

Abstract:This paper introduce the homological dimensions with respect to preresolving subcategories of an abelian category, discuss some properties about the homological dimensions. Next give the difinition and ues about the X-Gorenstein projective dimension and X-Gorenstein injective dimension of R-modules.

Key words:preresolving subcategories, homological dimension, generator, elementary method, conjecture

作者简介：郭娇霞(1988-),硕士生,研究方向：同调理论.

基金项目：国家自然科学基金(11361051).

收稿日期：2015-11-12.

DOI：10.3969/j.issn.1008-5513.2016.01.010

中图分类号：O178

文献标识码：A

文章编号：1008-5513(2016)01-0067-08