广义Camassa-Holm方程的几种新结论
伊丽娜,包俊东,套格图桑
(内蒙古师范大学数学科学学院,内蒙古呼和浩特 010022)
广义Camassa-Holm方程的几种新结论
伊丽娜,包俊东,套格图桑
(内蒙古师范大学数学科学学院,内蒙古呼和浩特010022)
摘要:给出一种辅助方程的几种新结论,构造了广义Camassa-Holm方程的多种无穷序列新解.首先,利用首次积分与函数变换,给出了一种辅助方程的新解、B¨acklund变换和解的非线性叠加公式.然后,通过函数变换,把广义Camassa-Holm方程的求解问题转化为非线性常微分方程的求解问题.最后,借助符号计算系统Mathematica,构造了广义Camassa-Holm方程的多种无穷序列新解.
关键词:广义Camassa-Holm方程;辅助方程;首次积分;多种新解
1 引言
1993年, Camassa和Holm在CH方程[1]中首次获得了尖峰孤立子解:
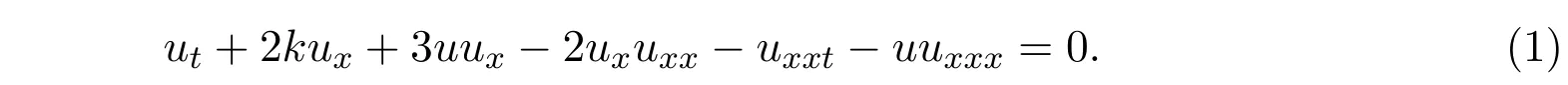
其中k是常数.
在Camassa-Holm方程中,发现尖峰孤立子解后在其他孤立子方程中不仅发现了此类新解,还发现了另外一种新解,即紧孤立子解.文献[2]推导出CH-r方程,并获得了尖峰孤立子解.
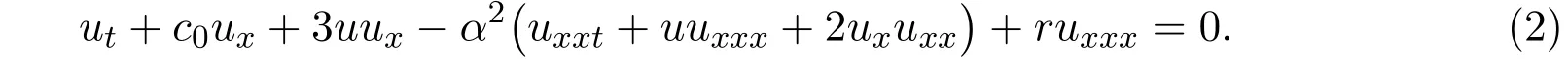
其中c0,α/= 0, r是常数.
文献[3-4]用定性分析理论,研究了Degasperis-Procesi方程(3)的求解问题,获得了尖峰孤立波解和周期尖波解.
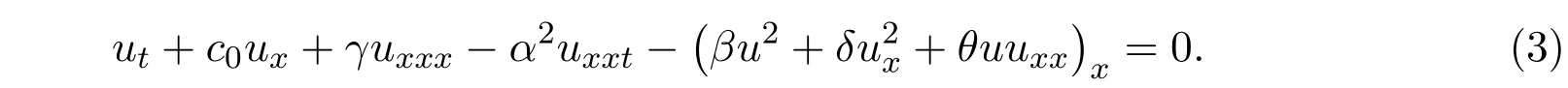
其中α,β,γ,δ,θ和c0均为常数.
文献[5-6]分别研究K(m,n)方程和B(m,n)方程,获得了三角函数型紧孤立子解.文献[7]用试探函数法,研究证明了广义Camassa-Holm方程(4)存在紧孤立子解.并获得了三角函数型紧孤立子解和双曲函数型孤立子解.
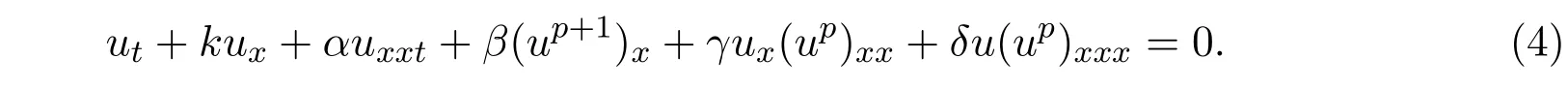
其中k,α,β,γ,δ和p均为任意常数.
当

时,广义Camassa-Holm方程(4)转化为Camassa-Holm方程(1).
广义Camassa-Holm方程(4)具有重要研究价值.本文用一种辅助方程的相关结论,通过几个步骤获得了广义Camassa-Holm方程的由双曲函数、Jacobi椭圆函数、Riemann θ函数、三角函数和有理函数组成的无穷序列新解.首先,利用首次积分与函数变换,给出了一种辅助方程的新解、B¨acklund变换和解的非线性叠加公式.然后,通过函数变换,把广义Camassa-Holm方程的求解问题转化为非线性常微分方程的求解问题.最后,借助符号计算系统Mathematica,构造了广义Camassa-Holm方程的多种无穷序列新解.
2 二阶非线性常微分方程的几种结论
下面给出一种二阶非线性常微分方程的新结论,并构造广义Camassa-Holm方程的无穷序列新解.

其中a,b,c是常数.
2.1二阶非线性常微分方程的首次积分
通过函数变换,可以把二阶非线性常微分方程(5)转化为一阶常微分方程组:
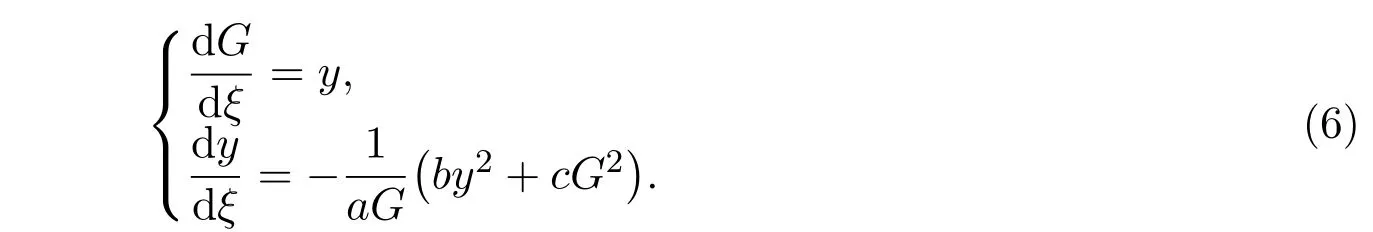
通过函数变换,将一阶常微分方程组(6)转化为下面的一阶常微分方程组:
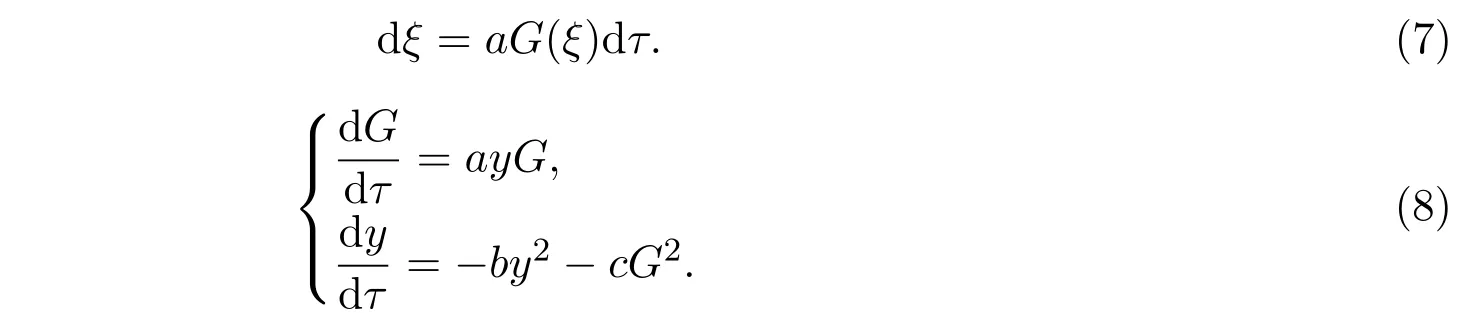
经计算获得了一阶常微分方程组(8)的如下首次积分:

这里m是任意常数.
将(9)式代入常微分方程组(8)的第一方程后得到下列常微分方程:
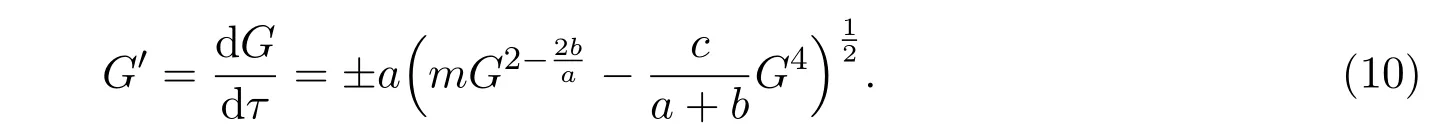
2.2常微分方程(10)的B¨acklund变换
下面分三种情况讨论,获得了常微分方程(10)的新结论.
定理2.1当b = 0时,方程(10)通过函数变换转化为下列Riccati方程:
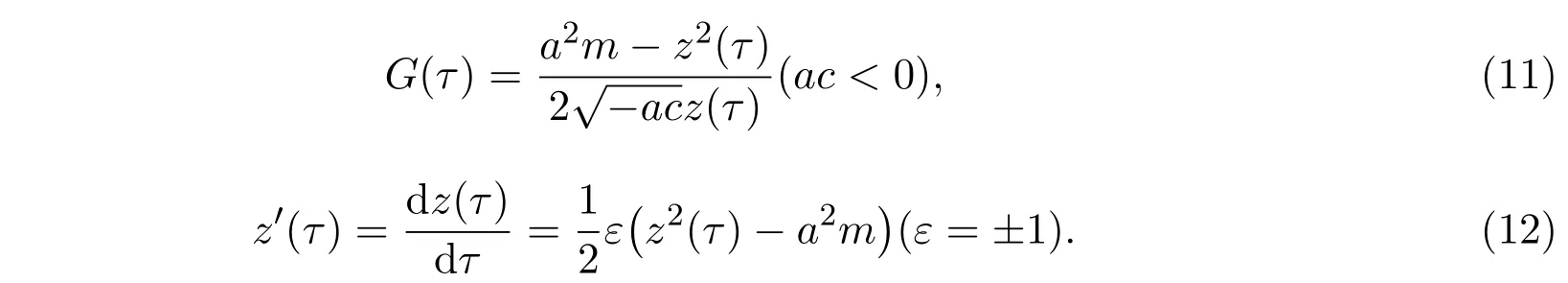
定理2.2当b = 0时,若G(ξ)是常微分方程(10)的非常数解,则下列也是常微分方程(10)的解.
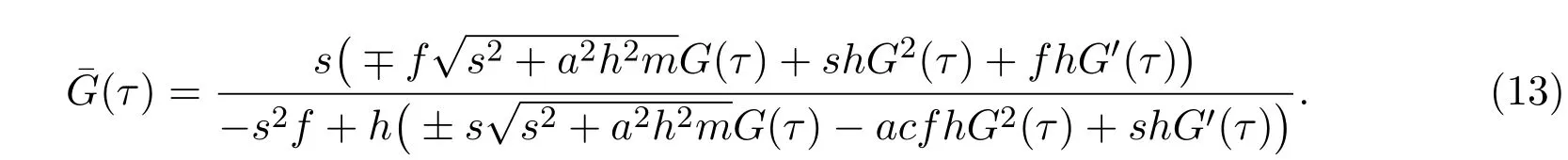
这里f, h, s是不全为零的任意常数.
定理2.3当b = 0时,常微分方程(10)存在下列解.
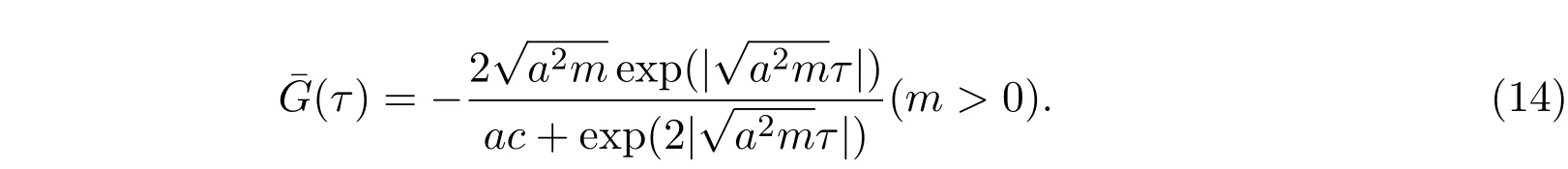
定理2.4当b = a时,若G(τ)是常微分方程(10)的解,则下列也是常微分方程(10)的解.
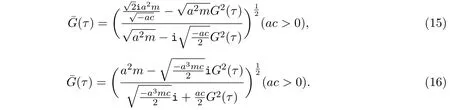
定理2.5当b = a时,常微分方程(10)存在如下解.



当a2m =θ24(0)θ22(0), ac = 2θ24(0)θ22(0),θ44(0) =θ42(0)时,

当a2m =−θ24(0)θ22(0), ac =−2θ24(0)θ22(0),θ44(0) =θ42(0)时,

这里
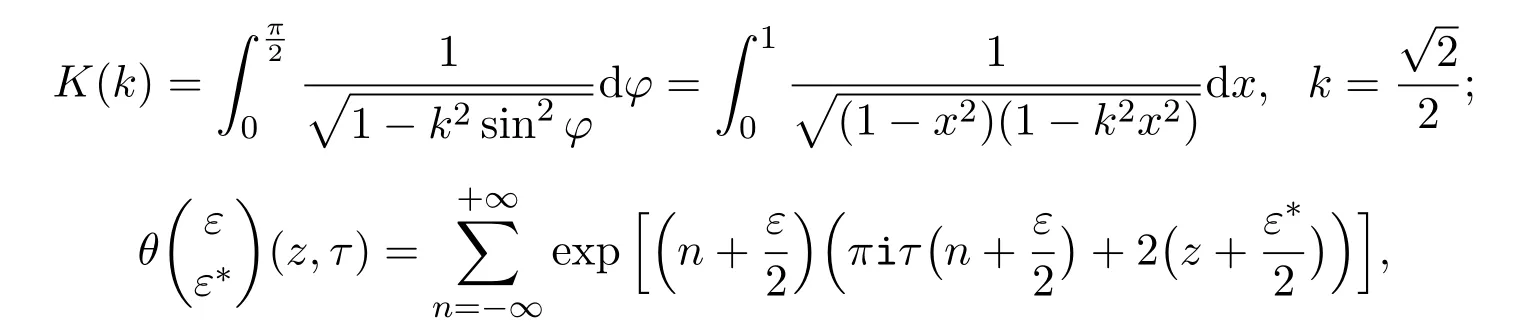
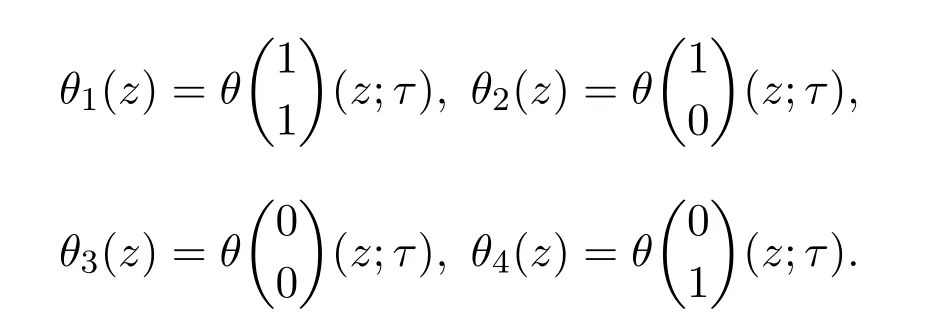
定理2.6当a =−2b时,方程(10)通过下列变换转化为如下Riccati方程:

定理2.7二阶非线性常微分方程(5)通过函数变换,转化为下面的Riccati方程:
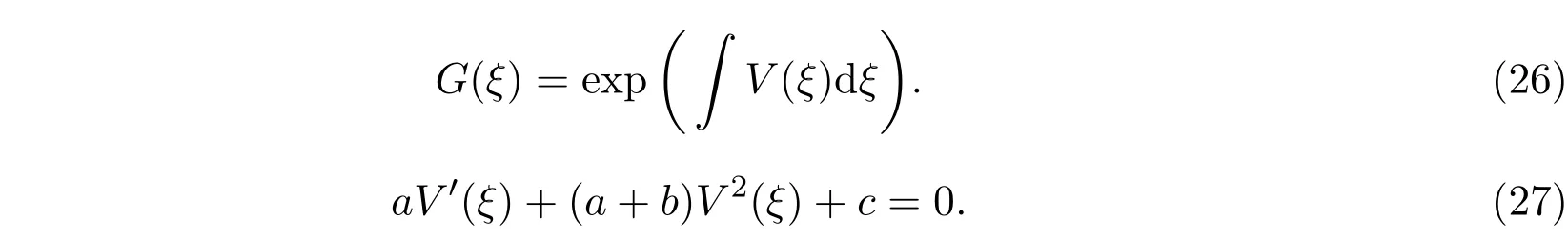
根据文献[9]中给出的有关结论,可以获得Riccati方程(27)的解、B¨acklund变换和解的非线性叠加公式(未列出).因而,通过函数变换(26),获得二阶非线性常微分方程(5)的无穷序列解.
3 广义Camassa-Holm方程的多种新解
将u(x,t) = u(ξ),ξ=µx+ωt(这里µ和ω是待定常数),代入广义Camassa-Holm方程(4)后得到下列非线性常微分方程
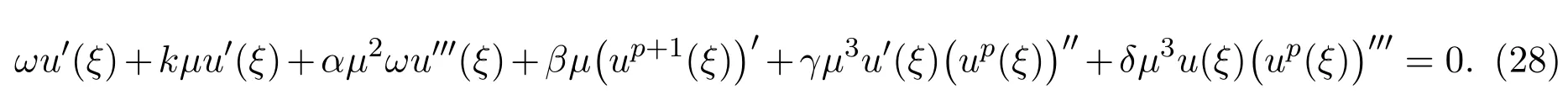
非线性常微分方程(28),通过下列函数变换,转化为如下非线性常微分方程:
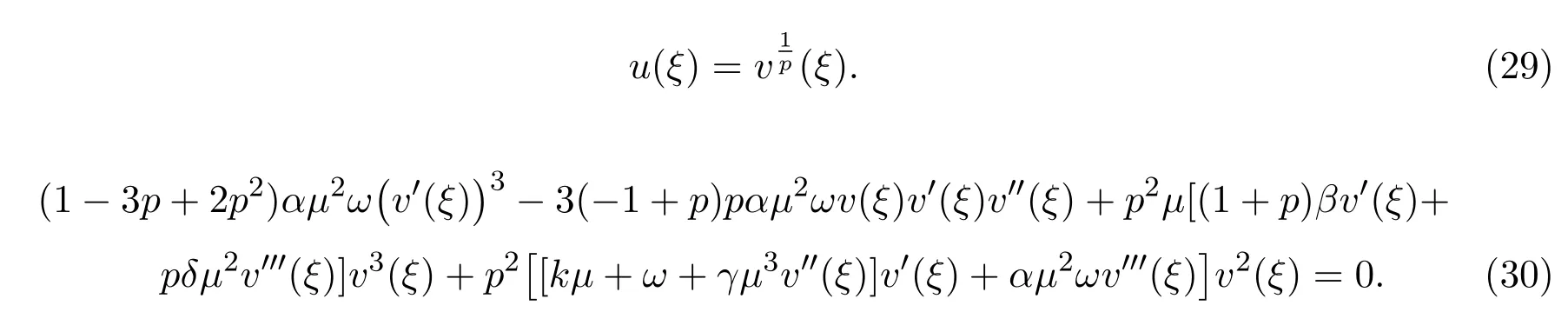
假设非线性常微分方程(30)的形式解为:

这里g0和g1是待定常数.
将(31)式与辅助方程(5)代入非线性常微分方程(30),并令
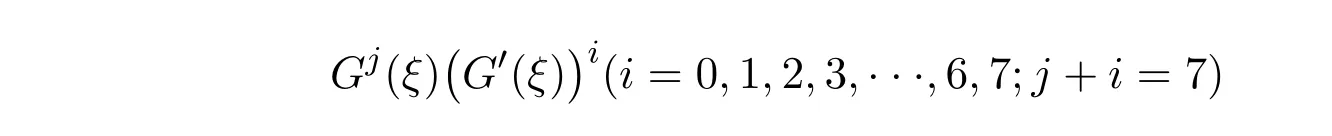
的系数为零后得到一个g0, g1, a, b, c,λ,µ,ω为未知量的非线性代数方程组(未列出).利用符号计算系统Mathematica求出该方程组的如下解:
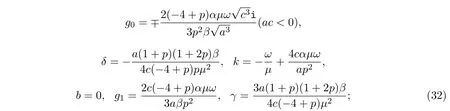

下面用代数方程组的解(32)-(35)和二阶非线性常微分方程(5)的相关结论,构造广义Camassa-Holm方程(4)的多种新解.
3.1广义Camassa-Holm方程的无穷序列类孤子新解
将(31),(32)式代入(29)后得到广义Camassa-Holm方程的如下形式解:
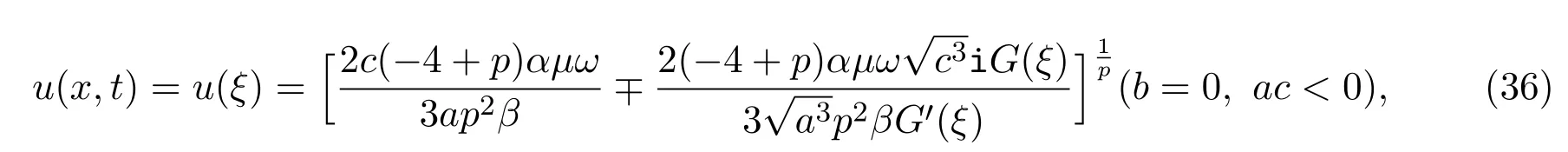
用定理1-定理3的结论,构造广义Camassa-Holm方程的由双曲函数、三角函数和有理函数组成的光滑孤立子解和双曲函数型尖锋孤立子解.
情形1通过下列叠加公式,构造广义Camassa-Holm方程的双曲函数型无穷序列新解.

情形2通过下列叠加公式,构造广义Camassa-Holm方程的三角函数型无穷序列新解.
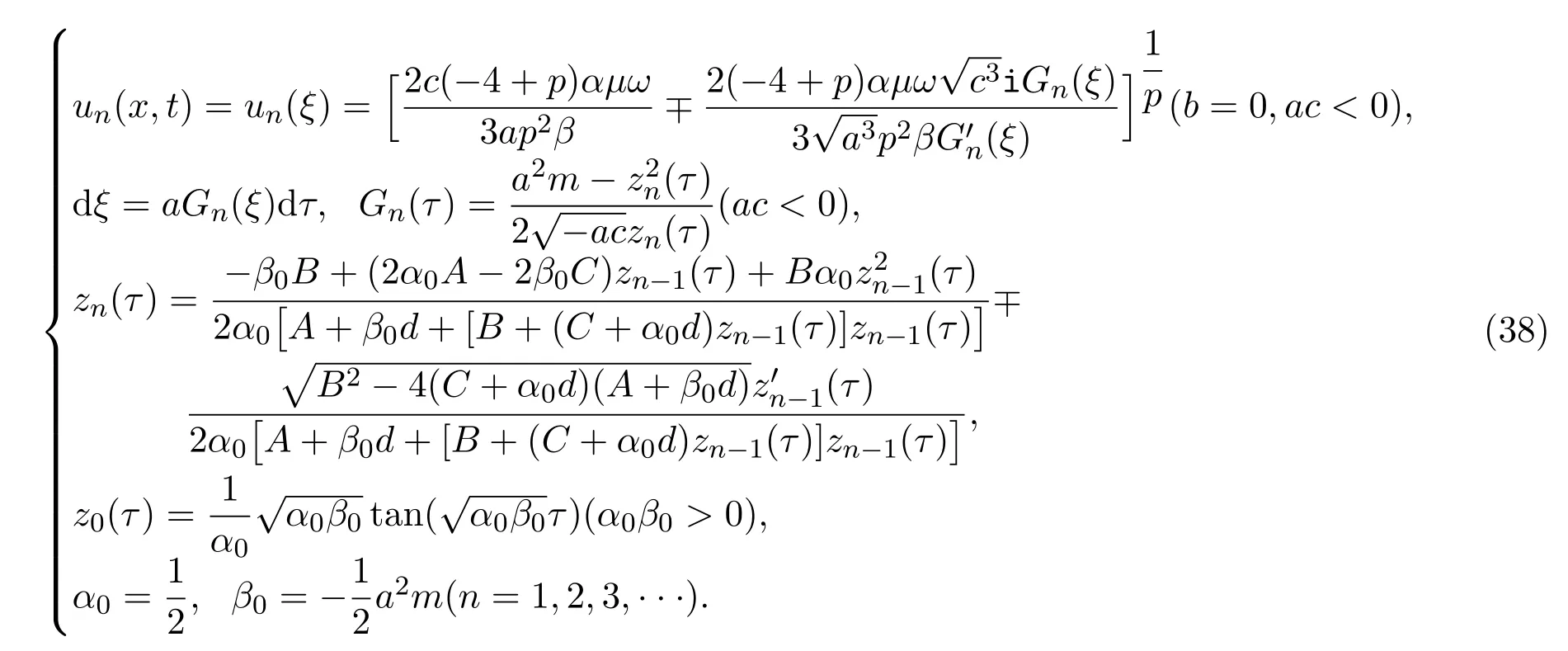
情形3通过下列叠加公式,构造广义Camassa-Holm方程的有理函数型无穷序列新解.

这里A, B, C, d是不全为零的任意常数.
情形4通过下列叠加公式,构造广义Camassa-Holm方程的指数函数型无穷序列尖锋孤立子新解.

这里f, h, s是不全为零的任意常数.
将(31)式, (33)式代入(29)式后得到广义Camassa-Holm方程的如下形式解:
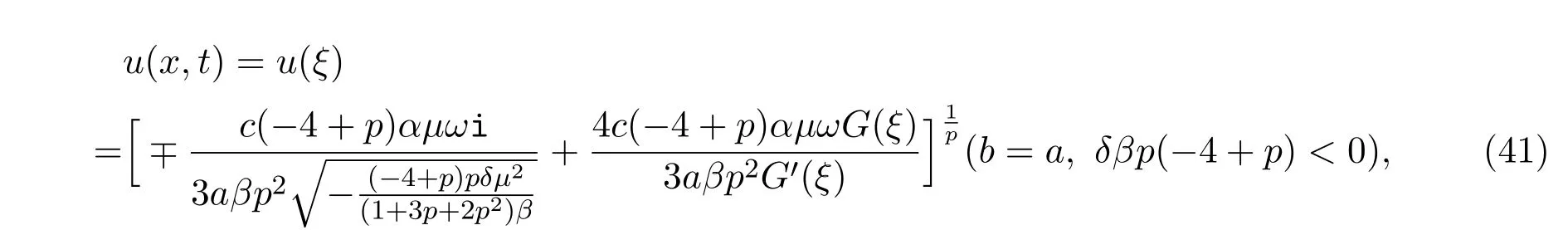
用定理1.4-定理1.5的结论,通过形式解(41),可以获得由Jacobi椭圆函数型紧孤立子解和Riemann θ函数和Jacobi椭圆函数组成的光滑孤立子解.
将(31)式,(34)式代入(29)式,后得到广义Camassa-Holm方程的如下形式解.
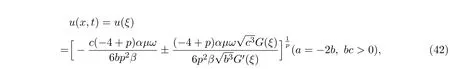
用定理1.6的结论,通过形式解(42),可以得到广义Camassa-Holm方程的有理函数型光滑孤立子解.
3.2广义Camassa-Holm方程的无穷序列孤子新解
将(31)式,(35)式代入(29)式后得到广义Camassa-Holm方程的如下形式解:
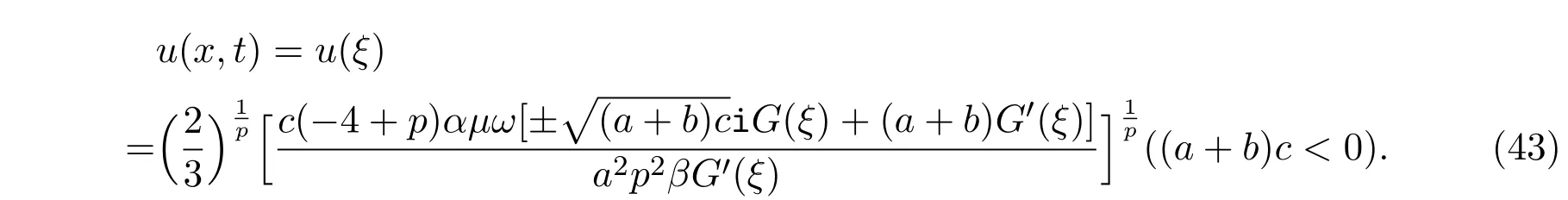
根据文献[9-11]中给出的有关结论,可以获得Riccati方程(27)的解、B¨acklund变换和解的非线性叠加公式(未列出).将获得的无穷序列解代入形式解(43)后得到广义Camassa-Holm方程的由双曲函数、三角函数和有理函数组成的光滑孤立子解(下面列出一个叠加公式).
通过下列叠加公式,可以获得广义Camassa-Holm方程的双曲函数无穷序列新解.
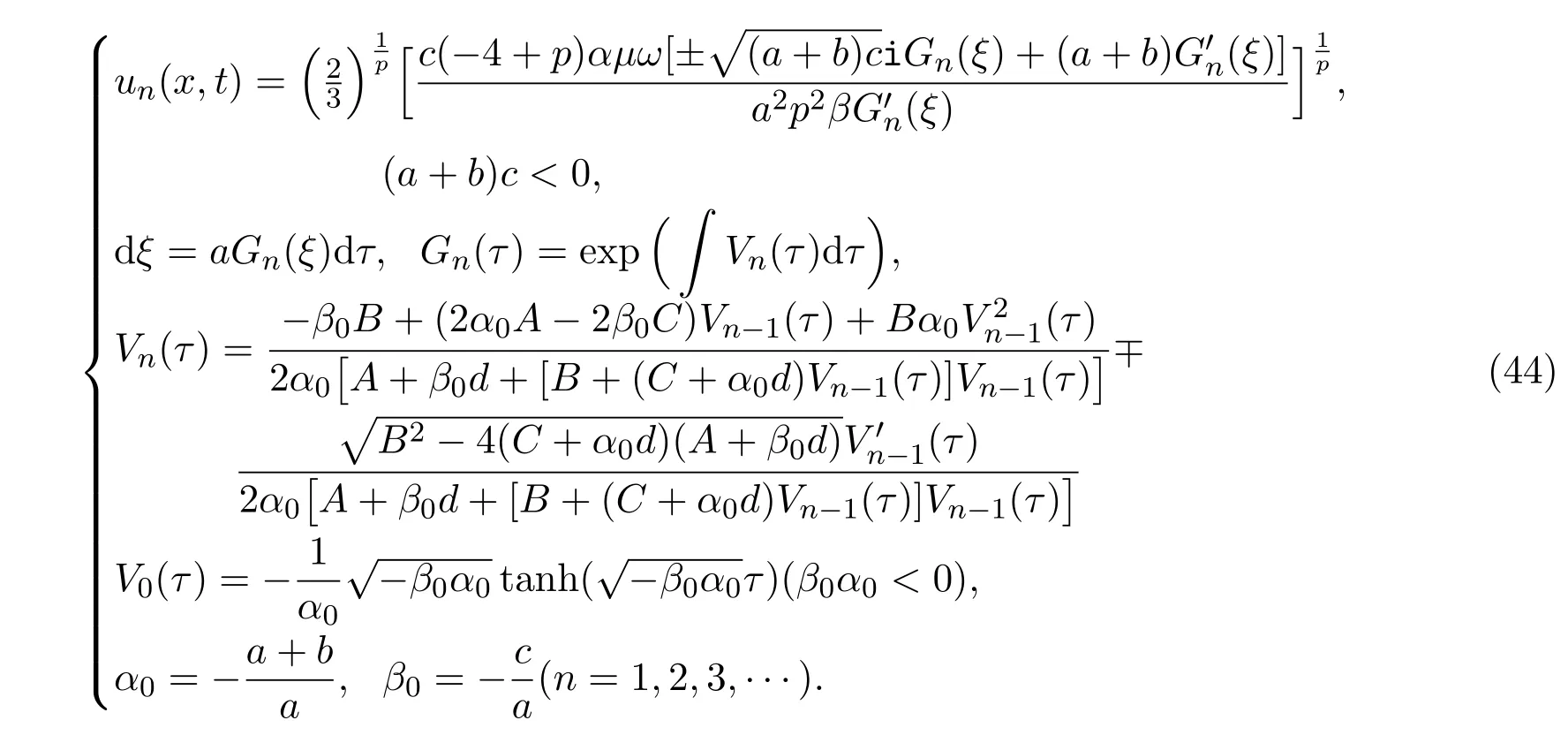
这里A, B, C, d是不全为零的任意常数.
4 结论
文献[7]用试探函数法,构造了广义Camassa-Holm方程的三角函数型紧孤立子解和双曲函数型光滑孤立子新解.本文在文献[8-19]的基础上,给出一种二阶非线性常微分方程的几种新结论.并用这些新结论与符号计算系统Mathematica,构造了广义Camassa-Holm方程的无穷序列类孤子新解.这些解包括由Riemann θ函数、Jacobi椭圆函数、双曲函数、三角函数和有理函数组成的无穷序列光滑孤子新解. Jacobi椭圆函数型紧孤立子新解和双曲函数型尖锋孤立子解.
参考文献
[1] Camassa R, Holm D D. An integrable shallow water equation with peaked solitons [J]. Phys. Rev. Lett., 1993,71(13):1661-1664.
[2] Boyd J P. Peakons and coshoidal waves: travlling wave solutions of the Camassa-Holm equation [J]. Appl. Math. Comput., 1997,81(2/3):173-187.
[3]余丽琴,田立新. Degasperis-Procesi方程的孤立尖波解[J].数学的实践与认识, 2006,36(3):261-266.
[4]余丽琴,田立新.带色散项的Degasperis-Procesi方程的孤立尖波解[J].纯粹数学与应用数学, 2005,21(4):310-316.
[5] Rosenau P, Hyman J M. Compactons:solitons with finite wavelength [J]. Phys. Rev. Lett., 1993,70(5):564-568.
[6] Yan Z Y, Bluman G. New families of solitons with compact support for Boussinesq-like B(m,n) equations with fully nonlinear dispersion [J]. Chaos, Solitons and Fractals, 2002,14:1151-1158.
[7]殷久利,田立新.一类非线性方程的compacton解及其移动compacton解[J].物理学报, 2004,53(9):2821-2827.
[8]王军民.修正的Korteweg de Vries-正弦Gordon方程的Riemann θ函数解[J].物理学报, 2012,61(8):1-5.
[9]套格图桑,白玉梅.非线性发展方程的Riemann theta函数等几种新解[J].物理学报, 2013,62(10):1-9.
[10] Taogetusang, Sirendaoerji, Li S M. Infinite sequence soliton-like exact solutions of the (2+1)-dimensional breaking soliton equation [J]. Commun. Theor. Phys. (Beijing), 2011,55(6):949-954.
[11] Taogetusang, Sirendaoerji, Li S M. New application to Riccati equation [J]. Chin. Phys., 2010,19(8):1-8.
[12] Khaled A, Gepreel, Saleh Omran. Exact solutions for nonlinear partial fractional differential equations [J]. Chin. Phys. B,2012,21(11):1-7.
[13] Md Nur Alam, Md Ali Akbar, Syed Tauseef Mohyud Din. A novel (G′/G)-expansion method and its application to the Boussinesq equation [J]. Chin. Phys. B, 2014,23(2):1-10.
[14] Chen Y, Li B, Zhang H Q. Generalized Riccati equation expansion method and its application to the Bogoyavlenskiis generalized breaking soliton equation [J]. Chin.Phys., 2003,12(9):940-945.
[15] Pan Z H, Ma S H, Fang J P. Instantaneous solitons and fractal solitons for a (2+1)-dimensional nonlinear system [J]. Chin. Phys. B, 2010,19(10):1-6.
[16] Li D S, Zhang H Q. The soliton-like solutions to the (2+1)-dimensional modified dispersive water-wave system [J]. Chin. Phys., 2004,13(7):984-987.
[17]马正义,马松华,杨毅.具有色散系数的(2+1)维非线性Schr¨odinger方程的有理解和空间孤子[J].物理学报, 2012,61(19):1-5.
[18]赵烨,徐茜.一类耦合Benjamin-Bona-Mahony型方程组的新精确解[J].纯粹数学与应用数学, 2015,31(2):12-17.
[19]祁新雷,李金花. (1+1)维Burgers方程新的行波解[J].纯粹数学与应用数学, 2008,24(4):709-712.
2010 MSC: 35Q51, 35Q58
Some kind of new conclusions of the generalized Camassa-Holm equation
Yi Li′na , Bao Jundong , Taogetusang
(The College of Mathematical Science, Inner Mongolia Normal University, Huhhot 010022, China)
Abstract:Some kinds of new conclusions of a kind of auxiliary equation are presented to construct the multiple new infinite sequence solutions of the generalized Camassa-Holm equation. First, with the help of the first integral and the function transformation, the new solutions of a kind of auxiliary equation, B¨acklund transformation and the nonlinear superposition formula of solutions are put forward. Then, by the function transformation, the problem of solving the solutions of the generalized Camassa-Holm equation is changed to the problem of solving the solutions of the nonlinear ordinary differential equation. Finally, with the help of symbols calculation system Mathematica, the multiple new infinite sequence solutions of the generalized Camassa-Holm equation are constructed.
Key words:generalized Camassa-Holm equation, auxiliary equation,first integral, multiple new solutions
作者简介:伊丽娜(1991-),硕士生,研究方向:复杂系统的稳定与控制.
基金项目:国家自然科学基金(11361040);内蒙古自治区高等学校科学研究基金(NJZY12031);内蒙古自治区自然科学基金(2015MS0128).
收稿日期:2015-09-25.
DOI:10.3969/j.issn.1008-5513.2016.01.007
中图分类号:O175.29
文献标识码:A
文章编号:1008-5513(2016)01-0045-10

