基于CP-FODT实时数据处理技术稳健性研究

梁红

(中国人民解放军91550部队，大连116023)

基于CP-FODT实时数据处理技术稳健性研究

梁红

(中国人民解放军91550部队，大连116023)

为改善飞行器实时数据处理中端点附近数据解算精度差、状态预估不准确的问题，提出并证明三次多项式一阶导数定理(CP-FODT)，对基于该定理的一阶导数解算方法的实时数据处理性能进行了研究.通过仿真计算研究了拟合区间长度、测量误差限及采样间隔对于计算结果的影响，对解算误差进行了分析，给出参数选取的基本原则，并采用实测数据对解算效果进行了验证.验证表明该算法对于实时数据处理具有较高的稳健性和可靠性，可提高端点附近数据的解算精度和预测的准确度，并可衍生为插值算法，能够为实时数据处理提供高精度的数据源.

三次多项式;一阶导数;实时数据处理;稳健性

0 引 言

稳健性是实时跟踪算法的重要性能指标，尤其是目标飞行当前位置，即跟踪段落端点附近数据的解算结果是否稳定，对于飞行轨迹的跟踪锁定和预测的准确度具有较大影响.因此，实时数据处理不仅要求算法快速、准确，而且还要具备良好的稳健性，能够适应飞行轨迹复杂多变的情况，以便实现对空间目标的有效监测识别、导航控制、态势估计等.

由于飞行轨迹的大机动特点以及对于数据的拟合模型有限的适应性，实时数据处理算法对于端点附近的数据处理一直是短板，主要问题是一阶导数估计精度不高，稳健性不能满足要求，高精度估计算法由于计算复杂［1］，难以满足实时处理需要.文献［2］和文献［3］对目前的实时数据处理算法进行了归纳和描述，主要是运动建模［4-6］和非线性滤波算法［1，7-10］.多源信息融合处理技术［11］充分应用目标的先验运动信息和各种测量信息对数据进行综合处理［12］.近年来，一些算法的融合和改进，使其性能不断提高［13-14］.这些研究工作为建立处理精度高、稳健性好、计算速度快的实时数据处理改进算法做出了重要贡献.

利用位置测量数据对速度进行估计或利用速度测量数据对加速度进行估计导数解算是实时跟踪测量方法的重叠内容.基于三次多项式的一阶导数定理(CP-FODT)是在差值定理［15］的应用研究过程中推导出来的，在本质上符合差值定理的驻点条件，因此，在用于一阶导数解算时，其准确度明显优于一般算法，尤其是对端点附近数据的解算，也拥有同样好的精度，这在文献［15］已有相关数据支持.

但该算法对于端点附近数据的稳定性研究目前尚未展开，解算结果受各参数的影响情况尚不明晰，算法对于测量误差的敏感程度还没有定量的描述，因此，基于CP-FODT的一阶导数解算方法对于实时数据的处理性能还有待研究.为此，本文基于仿真数据和实测数据，专门对该算法用于实时数据处理的稳健性进行了分析和探讨.

1 三次多项式一阶导数定理

式中，f(ti+1)表示端点的测量值，f(ti－1)表示端点的内邻点的前一点的测量值，A3表示对包括端点及其内邻点的拟合区间进行最小二乘三次多项式拟合的三次项系数，h表示采样间隔.

根据三次多项式一阶导数定理，可计算滤波区间的端点的内邻点的一阶导数.

2 仿真计算与讨论

2.1 算法的正确性验证

由表1的数据可看出，对于由三次多项式函数构造的仿真数据，按照三次多项式一阶导数定理，能够对其一阶导数进行准确解算，误差为0，表明该算法正确.

2.2 算法的基本性能

2.2.1 拟合区间长度对计算结果的影响

计算端点的内邻点(t=49)的一阶导数，结果列入表3.

由表3中的数据可看出，在采样间隔不变的情况下，随着拟合区间长度的缩短，t=49的点的一阶导数的计算误差越来越小，解算结果越来越接近真值.这是因为拟合区间长度越短，三次多项式拟合的准确度就越高，三次项的系数就越准确，一阶导数的解算结果也就越准确.

由表3中的数据还可看出，当拟合区间的长度发生较大变化时，对拟合精度的影响并不是很大，这主要是由数据本身的特点所决定的.这表明，该算法对于端点附近数据的解算具有良好的稳健性.

2.2.2 测量误差限与采样间隔对计算结果的影响

表1 采样间隔为0.5的仿真数据Tab.1 Simulation data(h=0.5)

表2 采样间隔为1的仿真数据Tab.2 Simulation data(h=1)

表3 t=49时的一阶导数解算结果Tab.3 Results of the first order derivative(t=49)

表4 t=45时的一阶导数解算结果Tab.4 Results of the first order derivative(t=45)

表5 t=45时的一阶导数解算结果Tab.5 Results of the first order derivative with differentSandh(t=45)

由表5可知，当A3一定时，一阶导数的解算误差不仅与采样间隔有关，也与测量误差限有关，而且在测量误差限不同时，解算误差对采样间隔的敏感程度也不同，当测量误差为0时，解算误差对采样间隔不敏感，且总体上较小.这说明测量数据越准确，一阶导数的解算结果就越准确.根据一阶导数的计算公式，一阶导数与测量误差限、采样间隔和三次拟合多项式的三次项系数有关，所以，表5中的数据所呈现出的特点是由这3个因素共同决定的.

3 误差分析及参数选取

3.1 误差分析

式中，Δf(ti+1)表示f(ti+1)的测量误差，Δf(ti－1)表示f(ti－1)的测量误差，Δh表示采样间隔误差，ΔA3表示A3的拟合误差.

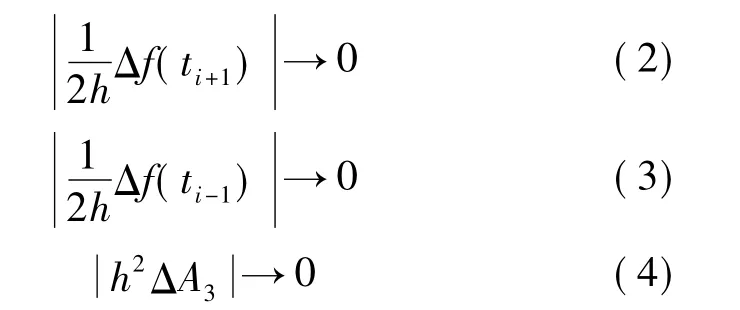
从而使|Δf'(ti)|→0.

3.2 采样间隔h的选取

由式(2)和式(3)可知，h→∞，由式(4)可知，h→0，这2个要求相互矛盾，为了在总体上获得较小的解算误差，折中取Δf(ti+1)、Δf(ti－1)、ΔA3的系数分别为1，使Δf(ti+1)、Δf(ti－1)、ΔA3既不扩大、也不缩小，在总体上保持稳定，则

故取0.5≤h≤1.

从表5中的数据可看出，当0.5≤h≤1时，一阶导数的解算误差虽然不是最小，但总体上的确处于小且相对稳定的状态，表明了上述分析的正确.

3.3 三次项系数A3的选取

从式(2)～(4)可看出，为了使|Δf'(ti)|→0，除了控制h的取值外，尽量减小测量误差和A3的拟合误差也很重要，因此，在计算时，应合理选取拟合区间长度，使A3的值尽可能准确.

4 算法的应用

4.1 实测数据解算

图1 飞行速度解算结果Fig.1 Results of flight velocity

图2 飞行速度解算误差Fig.2 Error of flight velocity

从图2中的速度解算误差来看，基于三次多项式一阶导数定理的一阶导数解算方法对于实测数据有比较好的应用效果，在整体上解算误差较小，在端点附近仍然有比较高的解算精度.

4.2 算法的实时性分析

以5点拟合区间为例，若计算机每计算一步所花费的时间是1 μs，则计算三次项系数所花费的时间约为92 μs，计算1点的一阶导数所花费的时间约为0.1 ms，远低于采样间隔，能够及时地为后续状态估计提供速度或加速度数据源，满足实时数据处理要求.

5 结 论

(1)采用基于三次多项式一阶导数定理的算法进行一阶导数解算时，所采用的数据间隔h和三次项系数A3对解算精度有影响，且当h在0.5和1之间时，解算结果在总体上误差较小.

(2)基于三次多项式一阶导数定理的一阶导数解算方法在实际应用时，首先选取适宜的拟合区间，对其进行最小二乘三次多项式拟合，获得拟合多项式的三 次 项 系 数A3，再 根据 式计算拟合区间中不包括端点的所需解算点的一解导数，然后将拟合区间向后移动，用上述方法继续计算.解算时，采样间隔一般应控制在0.5～1之间.

6 展 望

基于三次多项式一阶导数定理的解算方法是一种新的数据平滑、滤波和预测方法，其基本性能稳健、可靠，受飞行轨迹、拟合区间长度等因素影响较小，是一种高精度的离散数据微分解算方法.将该算法用于实时数据处理时，主要可在3个方面发挥作用:一是可对位置测量数据进行解算，获得拟合区间内不包括端点在内的任一点的速度;二是可对速度测量数据进行解算，获得拟合区间内不包括端点在内的任一点的加速度;三是从计算公式可看出，计算某点的一阶导数时，不需要该点的信息，利用这一特性，可对实时跟踪的失锁数据进行一阶导数插值.利用该算法的一阶导数解算结果，还可进一步利用其它算法进行后续的飞行器运动轨迹状态估计和预测.

基于三次多项式的一阶导数定理是在差值定理的应用研究过程中推导出来的，虽然在一阶导数解算过程中只用到三次多项式，但却能够比普通算法更好地适应更高阶次的数据［15］，如果在实时数据处理中成功应用，那么不仅能够适应飞行轨迹的大机动变化，减少或消除目标跟丢情况，实现对飞行轨迹的预测和有效跟踪，而且无须建立复杂的动力学模型和目标受力的先验信息，实时处理算法可大大简化.因此，在这方面还可做更多的研究，以便其早日进入应用阶段.

［1］SANJEEV A M，SIMON M，NEIL G，et al.A tutorial on particle filters for online nonlinear/non-gaussian bayesial tracking［J］.IEEE Transactions on Signal Processing，2002，50(2):174-188.

［2］刘也.弹道目标实时跟踪的稳健高精度融合滤波方法［D］.长沙:国防科学技术大学，2011.LIU Y.The robust and high accurate fusion filter for trajectory target realtime tracking［D］.Changsha:National University of Defense Technology，2011.

［3］李宏博.高频雷达目标数据处理技术研究［D］.哈尔滨:哈尔滨工业大学，2009.LI H B.Study of target data processing for high frequency radar［D］.Harbin:Harbin Institute of Technology，2009.

［4］LI X R，VESSELIN P J.A survey of maneuvering target tracking—PartⅡ:ballistic target models［C］//Proceedings of SPIE Conference on Signal and Data Processing of Small Targets.Washington D.C.:SPIE，2001:1-23.

［5］GREEN P J，SILVERMAN B W.Nonparametric regression and generalized linear models［M］.London:Chapman and Hall，1994:17-21.

［6］高羽，张建秋，尹建君.机动目标的多项式预测模型及其跟踪算法［J］.航空学报，2009，30(8):1479-1489.GAO Y，ZHANG J Q，YIN J J.Polynomial prediction model and tracking algorithm of maneuver target［J］.Acta aeronautica ET Astronautica Sinica，2009，30(8): 1479-1489.

［7］潘泉，杨峰，叶亮，等.一类非线性滤波器——UKF综述［J］.控制理论与决策，2005，20(5):481-489.PAN Q，YANG F，YE L，et al.Survey of a kind of nonlinear filters—UKF［J］.Controland Decision，2005，20(5):481-489.

［8］柴霖，袁建平，罗建军，等.非线性估计理论的最新进展［J］.宇航学报，2005，26(3):380-384.CHAI L，YUAN J P，LUO J J，et al.New developments in nonlinear systems estimation［J］.Journal of Astronautics，2005，26(3):380-384.

［9］TOR S S.A finite-difference method for linearization in nonlinear estimation algorithms［J］.Automatica，1997，33(11):2053-2058.

［10］MAGNUS N，NIELS K P，OLE R.New developments in state estimation for nonlinear system［J］.Automatica，2000，36(11):1627-1638.

［11］陈科文，张祖平，龙军.多源信息融合关键问题、研究进展与新动向［J］.计算机科学，2013，40(8):6-13.CHEN K W，ZHANG Z P，LONG J.Multisource information fusion:key issues，research progress and new trends［J］.Computer Science，2013，40(8):6-13.

［12］刘也，余安喜，朱炬波，等.弹道目标实时跟踪中的滤波方法综述［J］.宇航学报，2003，34(11):1417-1426.LIU Y，YU A X，ZHU J B，et al.Survey of filter algorithms for ballistic target real-time tracking［J］.Journal of Astronautics，2003，34(11):1417-1426.

［13］吴楠，孟凡坤，周致远.基于样条拟合和双向滤波的助推段弹道估计［J］.飞行器测控学报，2014，33(5): 392-398.WU N，MENG F K，ZHOU Z Y.Trajactory estimation in boost phase based on spline fitting and bidirectional filtering［J］.Journal of Spacecraft TT＆C Technology，2014，33(5):392-398.

［14］王勋.无人机自主跟踪地面运动目标方法与试验研究［D］.长沙:国防科学技术大学，2012.WANG X.An unmanned aerial verial vehicle autonomously tracking ground moving targets:algorithm and experiments［D］.Changsha:National University of Defense Technology，2012.

［15］梁红.利用差值定理降低飞行器速度和加速度拟合的截断误差［J］.飞行器测控学报，2005，24(3):51-54.LIANG H.Using Error Theorem to reduce the truncation error produced in calculating the velocity and acceleration of spacecraft［J］.Journal of Spacecraft TT＆ C Technology，2005，24(3):51-54.

Robustness of an CP-FODT-Based Algorithm for Real-Time Data Processing

LIANG Hong
(People’s Liberation Army Unit 91550，Dalian 116023，China)

To improve the precision in calculation and state prediction of real-time data near the endpoints of measurement sequence，the cubic-polynomial first-order-derivative-theorem(CP-FODT)is put forward and proved，and a new algorithm based on CP-FODT is researched for calculating the first order derivative of real-time data.How the sampling length，measure error bounds and sampling interval affect the results is shown by simulation calculation.The errors are analyzed，and some basic principles of parameter selection are given.Verification of the algorithm is made by measurement，and the results indicate that it is very robust and reliable.Not only can this algorithm improve the precision in calculation and state prediction of real-time data near the endpoints of measurement sequence，but also some interpolation algorithms can derive from it.So，it can provide high accurate data.

cubic polynomial;first-order derivative;real-time data processing;robustness

V557，O29

:A

:1674-1579(2016)02-0043-06

10.3969/j.issn.1674-1579.2016.02.008

梁 红(1971—)，女，高级工程师，研究方向为试验数据处理.

2015-10-28