一种火星进入段在线脱敏轨迹设计方法*
龙 也,刘一武
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
一种火星进入段在线脱敏轨迹设计方法*
龙 也1,2,刘一武1,2
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
为降低轨迹求解难度,提升脱敏制导的适应性,针对火星进入段提出一种在线脱敏轨迹设计方法.首先,采用预测的末端航程偏差和状态敏感度作为性能指标,利用该指标为倾侧角凸函数的特性将最优求解问题转换为简单的动态寻优过程;其次,结合任务要求和估计的进入点状态,通过迭代得到同时满足航程和横程要求的三自由度脱敏轨迹.仿真表明该方法可达到与现有脱敏设计相近的末端状态精度.
鲁棒制导;在线脱敏设计;火星进入段制导;脱敏最优控制
0 引 言
目前,火星进入、下降和着陆过程制导、导航与控制技术的研究聚焦于如何实现0.1 km精确着陆精度[1].其中,进入段是气动环境最恶劣、高度跨度最大,参数变化及不确定性最多的阶段[1],其末端状态精度对实现精确着陆非常关键,研究针对该阶段的高精度鲁棒制导方法具有重要意义.
进入段制导方法主要分为两类:标称轨迹制导和预测校正制导.第一类方法根据特定性能指标离线优化得到标称轨迹,进入过程中采用反馈线性化+PID[2]、滑模[3]等控制律跟踪标称轨迹,对模型不确定性具有一定的鲁棒性,但对进入状态偏差通常较为敏感.基于脱敏最优控制的制导方法[4-6]可较好地解决该问题,它通过在性能指标中添加特定形式的“系统对状态扰动敏感度”罚项,获得具有脱敏特性的标称轨迹,对进入偏差和过程扰动有较好的鲁棒性能,但其敏感度罚项由敏感度传播方程经积分、卷积得到,很难实现轨迹的快速求解.第二类方法采用数值或解析方法对末端状态进行预测,通过校正过程消除预测偏差,从而得到可行轨迹和实时控制指令,对进入状态偏差鲁棒,但迭代求解过程计算量大,需要较高的实时运算能力[7].
本文在现有脱敏设计基础上,综合标称制导实时计算量小及预测校正制导能在线求解可行轨迹的优点,针对三自由度脱敏轨迹的在线设计进行研究.
1 预备知识
1.1 动力学模型
忽略自转影响的三自由度火星进入段动力学方程如下[8]:

式中,r为探测器到火星中心距离,v为速度,γ为航迹倾角,s为待飞航程,θ为经度,λ为纬度,ψ为航迹方位角,g=μ/r2为探测器所处位置的重力加速度,μ为火星引力常数,σ为倾侧角.L和D分别为气动升力和阻力加速度:

式中,ρ为火星大气密度,采用标准指数型大气模型ρ=ρsexp[-(h/hs)],h=r-rM为所处位置高度,rM为火星半径,ρs为火星表面大气密度,hs为火星大气尺度高度,CL和CD分别为气动升力和阻力系数,Sr为探测器参考面积,m为探测器质量.此外,也可采用以下方法计算L、D:

式中,B为弹道系数,Γ为升阻比系数.
受限于探测器本身物理参数极限及开伞安全要求,进入段过程中需考虑最大过载、动压、热流率等约束[9]:

其中,nmax、qmax、等为前述约束的最大容许值,kq、rn、N、M为热流率计算相关系数.
对于标称制导的轨迹设计,轨迹除需满足前述基本过程约束,还需满足以下基本起终端约束:1)轨迹状态初值为标称进入点状态;2)轨迹末端状态包括高度、速度、航程、经纬度(横纵程),与预期值一致.此外,不同制导方法通常采用不同性能指标对满足基本约束的可行轨迹进行评价,优化过程以求解性能最优的轨迹为目标.
1.2 现有脱敏设计
现有脱敏设计采用纵向或三自由度动力学方程,但目标函数中的敏感度罚项均由纵向敏感度传播方程得出[5-6]:

式中,S(t|t0)=x(t)/x(t0)表示系统状态向量x=[rvγs]T的t时刻值对初始值x(t0)的敏感程度,u=cosσ为控制输入,f(x,u)为式(1)~(4)右侧项式.跟踪控制律:

式中,u*(t)和x*(t)分别为t时刻的标称控制量和标称系统状态,K(t)为状态反馈增益阵,η(t)为反馈增益乘子.
按式(15)积分得到轨迹各处的敏感度后,根据不同设计目标[4-5]计算敏感度罚项,进行离线的轨迹优化,即可获得相应脱敏特性的标称轨迹.
2 在线脱敏轨迹设计
现有方法的主要问题在于其末端约束的满足、轨迹敏感度的优化均依赖于单次的全局最优求解过程.作为对照,文献[7]采用幅值关于能量线性的倾侧角剖面对轨迹进行参数化,求解使末端航程预测偏差为0的倾侧角,从而得到可行轨迹和实时指令.衍生的阻力加速度制导方法[10]采用三段线性的阻力加速度剖面,通过调整中间段值满足末端航程约束,通过迭代航程和反转点得到满足末端横程约束的三自由度轨迹.因此,标称剖面的参数化以及末端约束的满足是实现在线设计的关键.
2.1 预测方程与轨迹参数化
预测方程采用类能量变量e=μ/r-v2/2作为独立状态替代时间t,由纵向动力学方程式(1)~(4)和敏感度传播方程式(15)除以=Dv得到:

倾侧角剖面采用文献[7]方法进行参数化,由待优化的当前倾侧角σp0和固定的末端倾侧角 σf确定:
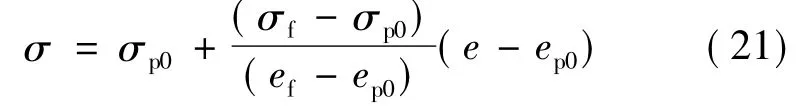
式中,ep0为当前能量值,ef为指定的末端能量值.
任意轨迹规划周期中,系统状态已知且σp0确定时,将式(21)代入式(17)~(20),从ep0积分到ef,即可得到预测的末端航程spf(σp0)及末端敏感度阵S(tpf|tp0),tp0为当前时间,tpf为预测的末端时间.
2.2 性能指标选择及动态寻优转换
规划过程中,算法根据状态约束和性能指标求解出每个规划周期的最优σp0值.其中,性能指标包含末端敏感度罚项,以优化末端对当前状态的敏感度,使轨迹具有末端对轨迹各处扰动不敏感特性.状态约束仅考虑末端航程,包括过载、热流率在内的其它约束通过更改初始倾侧角和标称进入状态处理[7].由于倾侧角剖面仅 σp0可调,航程约束spf(σp0)=0采用罚项形式出现在性能指标中:

式中,λ1≥0为敏感度权重,J1=|spf|为末端航程偏差罚项,J2为末端敏感度罚项:

式中,Si,j(tpf|tp0)为敏感度矩阵 S(tpf|tp0)的第i行第j列个元素,ci≥0,i=1,2,3,4为权重因子,表示对各状态脱敏特性的注重程度.

图1 不同能量值下性能指标J与σp0的关系Fig.1 Relation between performance indexJand σp0corresponding to different energy level
定义归一化能量E=(e-e0)/(ef-e0),e0为估计的进入点能量值,由图1可知,进入过程中,对于E的不同值,J均为σp0的凸函数.因此,规划周期fs较小时,结合倾侧角调整速率限制,可将逐个周期的最优σp0求解问题,转换为如下动态寻优过程:

式中,σp0(N)为上一周期的σp0值,σp0(N+1)为当前σp0寻优结果,为待选性能指标,为最大倾侧角速率.此外,式(24)得到的σp0如为负值则令σp0=0.
由初始倾侧角σ0出发,按式(24)递推即可得到纵向轨迹和倾侧角幅值剖面.敏感度罚项的引入会使末端航程出现偏差,即sf≠0,该问题在后续反转点的迭代求解过程中进行补偿.式(24)结果并非精确的最优解,但fs较小时差异可以忽略.
2.3 反转点求解及末端偏差消除
获得纵向轨迹和倾侧角幅值剖面后,为得到三自由度轨迹,需解决以下问题:1)找到合适的倾侧角反转时间点,消除末端横向偏差.2)补偿敏感度罚项引起的末端航程偏差,并消除纵向偏差.
反转时间点tinv通过牛顿迭代求解,公式为:
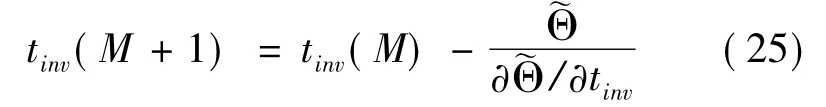
式中,tinv(M)为上一次迭代得到的tinv,tinv初始值可设为tf/2,tf为纵向轨迹的末端时间,为末端横向偏差,偏导通过有限差分方法近似获得.进行迭代时,均保留反转点前的倾侧角幅值剖面,按三自由度模型推演至反转点,并按式(24)对后续轨迹进行三自由度的重规划以更新.重规划过程中,由式(24)求解得到的σp0均取负,并考虑反转过程中倾侧角的调整速率限制.
末端航程偏差的补偿及纵向偏差的消除,均通过在上述迭代过程中更改初始待飞航程s0实现:
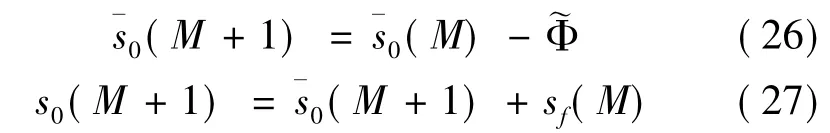
3 仿真分析
3.1 仿真参数
轨迹设计及蒙特卡洛仿真参数见表1~3.
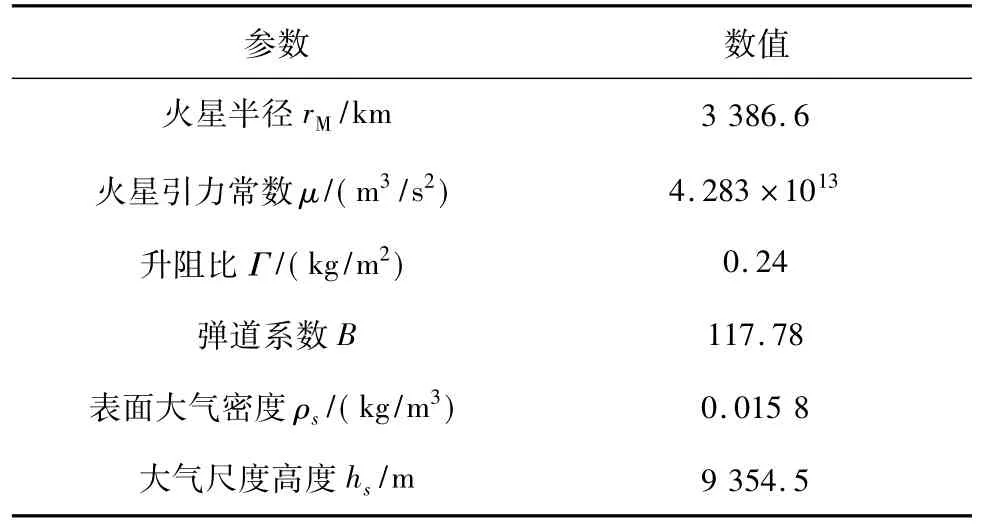
表1 相关物理参数[11]Tab.1 Related physical parameters

表2 过程约束参数[1]Tab.2 Process constraint parameters

表3 标称进入点与理想开伞点参数[11]Tab.3 Nominal entry point and ideal parachute deploy point parameter
此外K=-[0.01 0.005 50 -0.001],σ0=0,=0,σf=70°,c1=0.1,c2=0.3,c3=0,c4=1.

表4 蒙特卡洛仿真参数Tab.4 Monte Carlo simulation parameters
3.2 轨迹设计结果
图2,图3,表5给出不同λ1值下的纵向轨迹设计结果.图4为λ1=0.8时的三自由度轨迹设计结果.表6给出相同计算性能条件下,采用本文与文献[6]方法分别设计三自由度轨迹所耗时长的对照结果.

图2 不同λ1值时所得纵向轨迹的倾侧角幅值剖面Fig.2 Bank angle magnitude profile of designed longitudinal trajectory corresponding to different λ1values
图2表明λ1较小时,倾侧角剖面较长时间内与仅考虑末端航程时所得剖面基本重合,但一定时间后偏离,λ1增大时偏离时间点提前,λ1=0.95时初期阶段即已偏离.图3表明λ1较小时轨迹末端敏感度改善效果不明显,λ1过大时末端敏感度反而上升,λ1=0.8时末端敏感度相对较低,说明相对于现有脱敏设计,本文方法中敏感度权重并非越大越好.表5表明λ1增大时,轨迹末端高度降低,末端航程偏差增大,因此有必要在设计过程中进行补偿.表6表明本文方法设计效率相比文献[6]显著提升,fs= 0.1 s时仅耗时9分钟左右,求解更精细轨迹时(fs=0.025 s)耗时半小时左右.

图3 不同λ1值时所得纵向轨迹的末端敏感度Fig.3 Terminal sensitivity of designed longitudinal trajectory corresponding to different λ1values

表5 不同λ1值时所得纵向轨迹末端状态Tab.5 Terminal state of designed longitudinal trajectory corresponding to different λ1values

图4 λ1=0.8时所得三自由度轨迹的倾侧角幅值剖面Fig.4 Bank angle magnitude profile of designed three degree of freedom trajectory corresponding to λ1=0.8

表6 三自由度轨迹设计效率对比Tab.6 Efficiency comparison of three degree of freedom trajectory design
3.3 蒙特卡洛仿真
图5为按文献[6]方法离线设计的脱敏轨迹的蒙特卡洛仿真结果,图6为λ1=0.8时,本文方法在线设计的脱敏轨迹的蒙特卡洛仿真结果.

图5 离线设计的三自由度脱敏轨迹蒙特卡洛测试结果[7]Fig.5 Monte Carlo test results of offline designed 3DOF desensitized trajectory
综合图5~6及表7可知,蒙特卡洛测试中,除横向偏差有一定程度增加外,本文方法与现有脱敏设计的末端状态精度接近.

图6 在线设计的三自由度脱敏轨迹蒙特卡洛测试结果Fig.6 Monte Carlo test results of online designed 3DOF desensitized trajectory

表7 不同方法末端状态偏差范围对照Tab.7 Terminal state deviation scope comparison corresponding to different methods
4 结 论
现有脱敏设计需离线求解标称轨迹,且耗时较长.本文提出一种在线设计方法,可根据任务要求及估计的进入点在线快速设计三自由度脱敏轨迹.仿真表明该方法具有较高的末端状态精度,但所得轨迹末端高度偏低,有待进一步改进.
[1]BRAUN R D,MANNING R M.Mars exploration entry,descent and landing challenges[J].Journal of Spacecraft and Rockets,2007,44(2):310-323.
[2]TU K Y,MUNIR M S,MEASE K D,Bayard D S.Drag-based predictive tracking guidance for Mars precision landing[J].Journal of Guidance,Control,and Dynamics,2000,23(4):620-628.
[3]DAI J,XIA Y.Mars atmospheric entry guidance for reference trajectory tracking[J].Aerospace Science and Technology,2015,45:335-345.
[4]SHEN H J,HANS S,RICHARD W P.Desensitizing the pin-point landing trajectory on Mars[C]//AIAA/ AAS Astrodynamics Specialist Conference and Exhibit.Washington D.C:AIAA,2008.
[5]LI S,PENG Y M.Mars entry trajectory optimization using DOC and DCNLP[J].Advances in Space Research,2011,47(3):440-452.
[6]龙也,刘一武.火星进入段纵向脱敏局限性分析与三自由度脱敏设计[J].宇航学报,2015,36(8): 861-868.LONG Y,LIU Y W.Limitation analysis of longitudinal desensitize method for Mars entry phase and three degree of freedom desensitize design[J].Journal of Astronautics,2015,36(8):861-868.
[7]LU P.Predictor-corrector entry guidance for low-lifting vehicles[J].Journal of Guidance,Control,and Dynamics,2008,31(4):1068-1075.
[8]MANRIQUE J B.Advances in spacecraft atmospheric entry guidance[D].Irvine:University of California,Irvine,2010.
[9]JOEL B,KENNETH D M.Reachable and controllable sets for planetary entry and landing[J].Journal of Guidance,Control,and Dynamics,2010,33(3):641-654.
[10]SARAF A,LEAVITT J A,Chen D T,et al.Design and evaluation of an acceleration guidance algorithm for entry[J].Journal of Spacecraft and Rockets,2004,41(6): 986-996.
[11]LI S,PENG Y M.Command generator tracker based direct model reference adaptive tracking guidance for Mars atmospheric entry[J].Advances in Space Re-search,2012,49(1):49-63.
An Online Desensitized Trajectory Design Method for Mars Entry Guidance
LONG Ye1,2,LIU Yiwu1,2
(1.Beijing Institute of Control Engineering,Beijing 100190,China;2.Science and Technology on Space Intelligent Control Laboratory,Beijing 100190,China)
To reduce the difficulties in trajectory optimization and improve the adaptability of desensitization guidance,a novel online desensitized trajectory design method is proposed for Mars entry.The weighted value of predicted terminal sail error and state sensitivity are adopted as performance indexes,which are actually convex functions of bank angle.Taking use of this property,the original optimization problem is converted into a simple dynamic optimizing process.Then,according to the mission requirement and estimated entry state,a three-degree-of-freedom desensitized trajectory that simultaneously satisfies the requirement for range and cross range can be found via iteration process.Numerical simulations show that the terminal state accuracy of the proposed method is close to the existing desensitization design.
robust guidance;online desensitization design;mars entry guidance;desensitized optimal control
V448.2
:A
:1674-1579(2016)02-0020-06
10.3969/j.issn.1674-1579.2016.02.004
龙 也(1990—),男,博士研究生,研究方向为航天器制导导航与控制;刘一武(1968—),男,研究员,研究方向为航天器制导导航与控制.
*国家自然科学基金资助项目(61403030).
2015-11-29

