基于向量对方法的柔性空间机械臂建模与仿真

林 倩，袁 军

(北京控制工程研究所，北京100090)

基于向量对方法的柔性空间机械臂建模与仿真

林 倩，袁 军

(北京控制工程研究所，北京100090)

针对柔性自由漂浮基座空间机械臂系统建模的过程中存在的形式复杂计算量大等问题，本文采用向量对方法，以自由漂浮基座双连杆柔性机械臂为研究对象，以单个体的动力学方程为基础，分别列出相邻两个体之间的约束方程，利用拉格朗日乘子法组装构成系统的动力学方程.这种方法在建模时需要的信息较少，易于推导，得到的方程十分规范化，更加有利于柔性空间机械臂控制系统的设计.最后文章通过仿真验证了模型的正确性.

柔性空间机械臂;动力学建模;向量对方法;刚柔耦合

0 引 言

空间机械臂是一类典型的飞行器操作系统，它可以在太空中对卫星等航天器进行维修装配等在轨服务，极大地延长了卫星的使用寿命，避免了重新发射一颗卫星以及回收旧卫星所带来的巨大消费［1-2］.因此，空间机械臂的研究具有非常重要的工程实际意义.空间机械臂具有质量轻，结构长，刚度低，结构阻尼弱等特点使自由漂浮空间机械臂系统成为了一种典型的刚柔耦合多体系统.用一般的方法建立动力学模型推导过程十分复杂，计算量大，得到的动力学方程不利于求解和控制系统的设计.因此本文根据系统的结构特点，采用一种更加方便有效易于推导的建模方法，为进一步的柔性空间机械臂控制系统的设计提供更有利的模型，并且通过仿真验证了模型的正确性.

对带柔性附件卫星的动力学研究已经历经了很长的时间，Kane等［3］在1987年提出了建立连接在移动基上的悬臂梁的动力学模型的方法.文献［4］将柔性影响视为加在刚体运动上的一个确定的扰动项，这样柔性运动可以以类似重力柯氏力以及向心力形式被处理.文献［5］研究了航天器大范围刚体运动与其挠性附件弹性变形运动的刚柔耦合动力学，并且对航天器的姿态控制方法和挠性附件的振动控制也进行了研究.对于多体系统，每个物体之间存在着一定的位置关系.本文研究只有一条通路的链式结构的自由漂浮基座空间机械臂系统，一般有两种描述向量关系的方法.一种是向量链的方法，这种方法求得的动力学方程是一种耦合型的动力学方程，包含全部广义坐标，可以方便提供控制系统设计所需的设计模型，缺点是求解时十分复杂，运算量很大.另一种方法是向量对的方法，这种方法得到的方程比较规范化，需要的信息较少，并且可以提高计算效率，满足实时仿真的需要［6］.在以往的针对柔性自由漂浮空间机械臂建模研究中，大多采用向量链的方法来描述系统中的向量关系，得到的方程十分复杂，不利于求解和仿真，更不利于控制系统的设计，因此本文采用向量对方法，利用第二类拉格朗日方程和拉格朗日乘子法建立多柔性体系统的动力学方程.

1 柔性臂杆弹性位移的描述

由假设模态法可以将柔性臂杆的弹性变形表示为［7］:

其中，Φ(x)=[φ1(x) φ2(x) … φn(x) ]T为假设模态，q(t)=[q1q2…qn]T，qi(t)为相应的广义坐标.

利用Lagrange方程可以求出广义坐标满足的微分方程

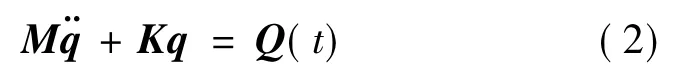
式(3)的解可以设为

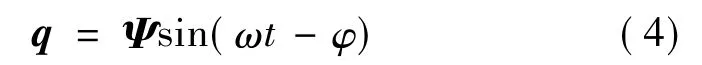
式中，Ψ是振幅向量，ω是振动圆频率，φ是相位角，将式(4)代入式(3)中可得，

由此得到n个特征值 λi和相应的特征向量Ψi，ωi就是原连续系统的n个固有频率的近似值，特征向量Ψi为与λi=对应的固有模态.可以得到归一化模态Ti:

其中，ai为模态质量可以由模态正交性得到，然后利用模态展开的方法将弹性位移uf表示为:

其中，T= [T1T2… Ti…]是由归一化模态Ti组成的模态阵，称为归一化模态阵，τT=(τ1，τ2，…，τn)是模态坐标矢量［6］.

这样，模态坐标矢量可以直接作为广义坐标纳入到系统的动力学模型当中，达到刚柔耦合的目的.

2 柔性空间机械臂系统的动力学建模

2.1 定义坐标系

对于柔性空间机械臂这样具有轻质、高速等特点的空间组合体结构，在进行动力学建模过程中一个重要的问题就是需要考虑结构的弹性变形与系统的大范围运动之间的耦合.本文采用混合坐标法和广义坐标来描述物体在空间中的位形.如图1所示:OXYZ为惯性坐标系，用以描述所有物体的刚性运动以及物体间的约束，其余坐标系均与本体固联，随着本体转动而转动.

图1 物理模型Fig.1 Model of the system

2.2 柔性臂杆Bi的动力学方程

柔性体i上任意一点Qi在惯性系中的位置矢量为:

其中，Ri是柔性体i的自身物体系的原点在惯性系中的位置矢量，ui是Qi点在物体系i中的位置矢量，是物体系i到惯性系的变换矩阵.由于柔性体质点间具有相对运动，因此存在弹性变形，设Qi点处的弹性变形矢量为，为不存在弹性变形时Qi点在物体系i中的位置矢量，则由图1的右侧图形可以得出

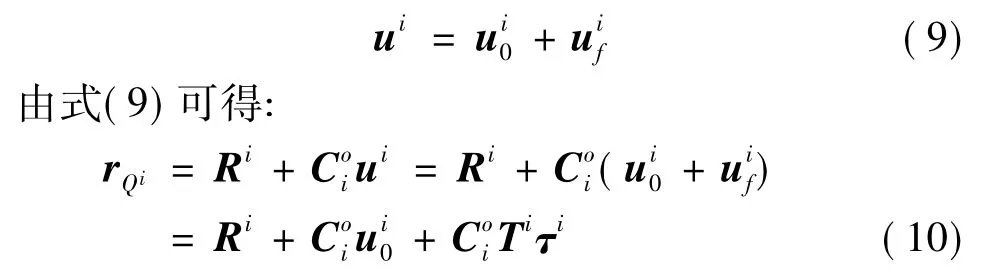
式(10)对时间求导可以得出柔性体i上任意一点Qi的速度矢量

令

在点Qi处取一体元，则物体i的动能表达式为

其中，ρi和Vi分别是点Qi所在体元的质量密度和体积，由于广义坐标与时间相关，式(18)可以写成

柔性体i在采用模态坐标表达弹性位移后，应变能可以用模态坐标表示为以下形式:

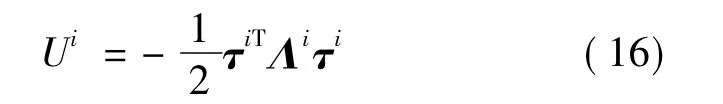
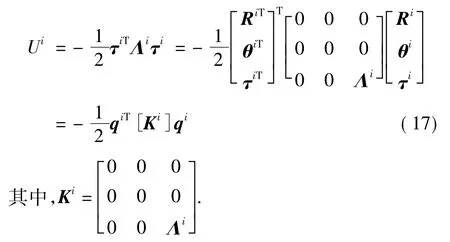
由上式可以得出作用在柔性体i上的总的广义力矢量:

再根据物体i的动能，代入Lagrange方程，得:

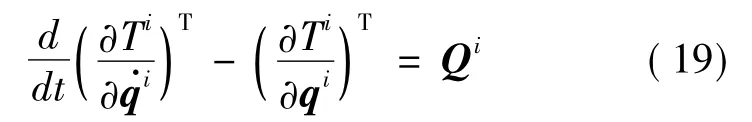
则柔性体i的动力学方程可表示为:

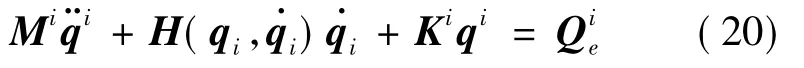
中心刚体A的动力学方程为

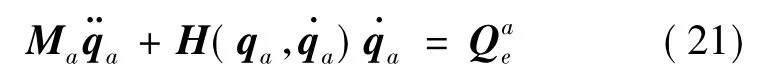
2.3 带有弹性位移的约束方程

本文以自由漂浮基座双连杆柔性空间机械臂为研究对象，只研究两个臂杆的情况.由多体系统的物理模型可知，中心刚体A和柔性臂杆B1之间由转动铰相连接，二者的重合点为点E;柔性臂杆B1和柔性臂杆B2之间由转动铰相连接，二者的重合点为点F，如图2所示.

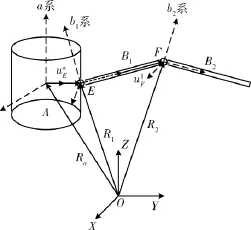
图2 物体间的约束Fig.2 Constraints between objects

将点E视为在物体A上，那么它在惯性系中的位置矢量由上面的推导可知

将点E视为在物体B1上，可以看到此时点E刚好在物体B1的固联坐标系的原点上，但是由于物体B1为柔性体，在原点处也会存在弹性位移，所以它在惯性系中的位置矢量为

式(24)也可以表示成:

即为A、B1之间的约束方程.

同理，将点F视为在物体B2上，点F也恰好在物体B2的固联坐标系的原点上，可知B1、B2之间的约束方程如下:

式(25)、(26)构成了系统的约束方程.

令

则由上面的两个方程组成的方程组可表示为

其中，

利用拉格朗日乘子法，可将约束方程与各个物体动力学方程组合在一起，得到自由漂浮基座柔性空间机械臂的动力学模型.

系统的动力学学方程可表示为:

由上面的推导可以得出，系统的动力学模型为:

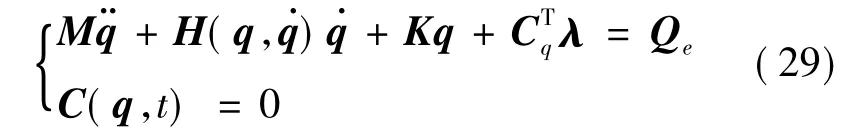
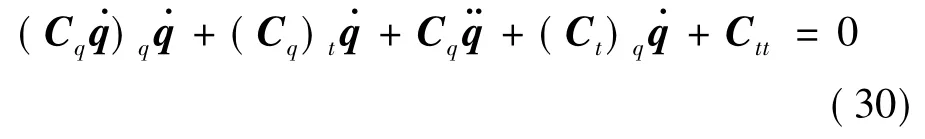
整理可得

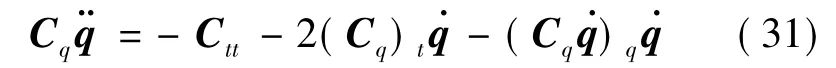
由于约束方程的存在，动力学方程的广义坐标分为独立的和非独立的，其中非独立广义坐标即相关广义坐标的个数等于约束方程的个数.独立坐标的数目等于广义坐标的总数减去相关坐标的个数，即系统的自由度［9］.将系统的独立坐标表示为qi，相关坐标表示为qc，则系统的全部广义坐标可表示为

将动力学方程分块表示:

另外可以得到:

可以得到相关坐标由独立坐标表示:

最终得到动力学模型:

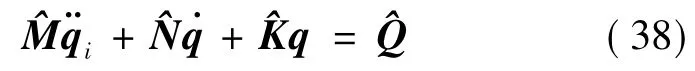
由推导过程和最终的得到的模型可以看出:采用向量对方法与向量链方法相比，需要的信息量较少，并且基于单个物体的动力学方程的基础上，十分易于推导，可避免推导过程中由于计算造成的失误，最终得到的方程十分规范化，更有利于数值仿真和控制系统的设计.

3 数值仿真

在仿真过程中通过假设两个臂杆在同个平面内转动来简化模型，因此进一步假设坐标系OaXaYaZa、Ob1Xb1Yb1Zb1、Ob2Xb2Yb2Zb2中的OaYaZa、Ob1Yb1Zb1、Ob2Yb2Zb23个平面共面，臂杆的转动只会引起卫星绕Xa轴转动.仿真的控制目的是给出期望关节角，通过控制使臂杆的关节角收敛到期望关节角，且激发的振动能得到很好的抑制.因此设计一种带有鲁棒项的PD控制器

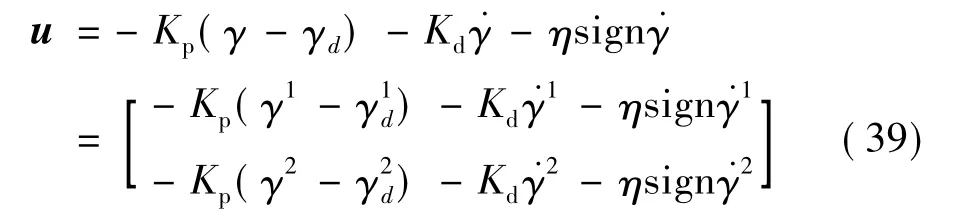
Kp和Kd分别为比例和微分系数，最末项为鲁棒项，用于消除建模误差，取η≥0.

仿真参数如下:卫星质量为300 kg;绕Xa轴转动惯量为800 kg·m2;卫星质心到机械臂与卫星连接处的距离为2 m.

假设两臂杆的各项参数完全相同，机械臂杆的各项参数如下:质量为6.4 kg;长度为4 m;对质心转动惯量为34.132 4 kg·m2;弹性模量为7.6× 1010N/m2;质心位置比为0.5;截面惯量矩为I= 1.26×10－7m4.

为简化计算，取悬臂梁边界问题的容许函数作为柔性臂杆的假设模态

取期望关节角 γd= [ π/3 π/3]T，Kp=300、Kd=1 000、η=0，两臂杆阻尼均设为0.01，得到仿真结果如图3～6所示.

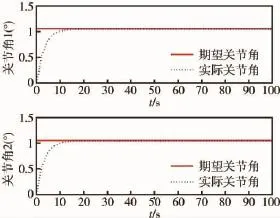
图3 关节角γ1和γ2的变化曲线Fig.3 Joint angelsγ1and γ2curves

图4 关节角γ1和γ2的角速度变化曲线Fig.4 Angular velocity curves of joint angels γ1and γ2

图5 机械臂杆1的一阶和二阶模态和速度曲线Fig.5 Arm 1 two modes and velocity curves

仿真结果表明，两个机械臂杆的关节角可以跟踪并收敛到期望值，角速度快速收敛到零，因此可以很好的实现机械臂的动作控制;由于臂杆的柔性存在，在臂杆进行动作的同时柔性臂杆产生了大幅度的振动，随着臂杆运动的停止，振动幅度也逐渐减小直至稳定，验证了模型的正确性.

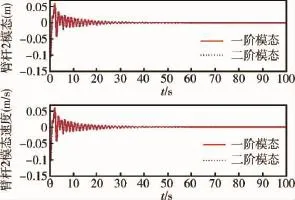
图6 机械臂杆2的一阶和二阶模态和速度曲线Fig.6 Arm2 two modes and velocity curves

4 结 论

文章通过假设模态法和模态展开法结合对柔性机械臂的弹性位移进行了描述，并利用向量对的方法对自由漂浮基座柔性空间机械臂进行了动力学建模，以个体的动力学方程为基础，考虑每两个相邻物体之间的约束方程，利用Lagrange乘子法建立多柔性体系统动力学方程，并通过仿真验证了模型的正确性.利用向量对的方法建立自由漂浮基座柔性空间机械臂的模型，得到的方程十分规范化，基于单个物体的动力学方程的基础上，十分易于推导，可避免推导过程中由于计算造成的失误，并且与普通的向量链方法相比，需要的信息量较少，仿真过程中的运算量较小，可以明显提高计算效率，可为进一步的柔性空间机械臂控制系统的设计提供更有利的模型.

［1］LONG A，RICHARDS M，HASTINGS D E.On-orbit servicing:a new vake proposition for satellite design and operation［J］.Jornal of Spacecraft and Rockets，2007，44(4):904-976.

［2］NASA，On-orbit satellite servicing study project report［R］.Technical Report，NASA，2010.

［3］KANE T R，RYAN R，BANERJEE A K.Dynamics of a cantilever beam attached to a moving base［J］.Journal of Guidance，Control，and Dynamics，1987，10(2): 139-151.

［4］BARUH H，TADIKONDA S S K.Issues in the dynamics and control of flexible robot manipulators［J］.Journal of Guidance，Control，and Dynamics，1989，12 (5):659-671.

［5］蒋建平.大挠性多体结构卫星刚柔耦合动力学研究［D］.长沙:国防科学技术大学，2004.

［6］黄文虎，邵成勋，等.多柔体系统动力学［M］.北京:科学出版社，1996，29-69.

［7］方同，薛璞.振动理论及应用［M］.西安:西北工业大学出版社，2000，270-277.

［8］MEIROVITCH L，HELSON H D.High spinmotion of scatellite containing elastic parts［J］.Spacecraft and Rocket，1996，13:1957-1062.

［9］孙世基，黄承绪.机械系统刚柔耦合动力分析及仿真［M］.北京:人民交通出版社，2000，140-164.

Dynamic Modeling and Simulation of Flexible Space Manipulator Based on Vector Pairs Method

LIN Qian，YUAN Jun
(Beijing Institute of Control Engineering，Beijing 100090，China)

The vector pairs method is adopted for dynamic modeling of a free-floating two-links flexible space manipulator system in this paper.On the basis of each body’s dynamic function，the constraint equations between each two connected objects are derived.These equations are assembled by Lagrange multiplier method and constitute the dynamic equations of the whole system.By using this method，the modeling process requires less information and the functions are easy to deduce.The final dynamic equations are very standardized and more appropriate to design control system.The validity of the dynamic equations derived by the method has been demonstrated by numerical simulations.

flexible space manipulator;dynamic modeling;vector pairs method;coupled rigid-flexible system

V414

:A

:1674-1579(2016)02-0026-06

10.3969/j.issn.1674-1579.2016.02.005

林 倩(1992—)，女，硕士研究生，研究方向为导航制导与控制;袁 军(1965—)，男，研究员，研究方向为导航制导与控制.

2015-11-03