基于动态分析的多面体模型非仿射扩展方法*

王建花，陈朝晖

(北京控制工程研究所，北京100190)

基于动态分析的多面体模型非仿射扩展方法*

王建花，陈朝晖

(北京控制工程研究所，北京100190)

多面体模型只能表示循环中访存数组下标可以用仿射表达式表示的循环，针对这个限制设计一种基于动态分析的方法对多面体模型的表示范围进行扩展.该方法利用程序运行时的动态信息，将循环非仿射表达式中的循环全局参数用定值替换，推测生成非仿射循环的参数定值化版本，使之可以被多面体模型表示.该方法扩展了多面体模型的表示范围，使更多的代码区域可以被并行优化，提高了程序中SCoP的覆盖率，提高了程序运行的加速比.实验证明了该方法的有效性.

并行编译;多面体模型;SCoP;仿射;动态分析

0 引 言

多面体模型优化方法是一种针对嵌套循环进行并行优化的编译技术.多面体模型将程序中的循环映射到数学上的多面体模型中，利用已经非常完备和正确的多面体理论做各种形式的变换，再将其重新映射回程序中的循环.它几乎覆盖了所有传统循环变换方法，并进一步完成一系列比较复杂的循环体优化，给出综合性的代码优化、并行化方案［1］.

程序中可以被多面体模型表示的代码区域称为静态控制体(static control part，SCoP)［2］，多面体模型从程序的控制流图中提取出SCoP，为它构建多面体模型表示，并在多面体模型上进行相应的转换.然而，一些代码区域由于不能满足SCoP的限制条件，从而无法被多面体模型表示优化.其中一个主要的限制条件是SCoP要求循环界限和访存数组下标必须可以用仿射表达式表示.静态分析时，程序中存在一些无法判断的代码情况，为了保证优化的正确性，静态优化技术对其保守估计［3］，不对其表示和优化，大大降低了可优化代码(SCoP)的覆盖率.

对多面体模型表示的进行了扩展非仿射限制，大致可以分为3类:第一类是对非仿射表达式分析，为其提供常规的表示，进而对其优化处理;第二类是将新的代数方法应用于多面体模型，使多面体模型可以表示非仿射表达式;第三类是使用动态分析技术，将在运行时间检测到的动态信息应用于对非仿射表达式的并行化优化.

文献［3］使用第一类方法扩大了多面体的表示范围，为每个非仿射的条件语句提供一个控制预判句.然而这个方法引入了条件变量对控制预判语句的依赖关系，降低了依赖分析的准确性.文献［4］和［5］使用量词消除方法处理代码转换过程和代码生成过程中的乘法参数.然而，该方法需要复杂的建模和转换阶段，可能使程序性能降低.Baghdal等［6］揭示了推测优化技术的巨大潜力，Jimborean等［7-8］将推测并行技术应用到多面体模型上.编译时间时假设循环界和数组下标是仿射的，生成程序静态并行化版本框架.运行时间时，若假设成立，则利用动态信息实例化静态并行版本，反之则回退执行原始的顺序版本.然而，该方法在多面体转换过程中不能改变程序语句的顺序，也不能改变循环的结构，大大限制了多面体的并行转换方式.文献［9］将检查/执行策略应用到多面体模型中，提出了一个循环转换架构.这个架构使用无解释函数(uninterpreted function)表示数组下标，结合程序运行时的具体数值建立函数映射关系.然而该方法仅能对只读的非仿射数组下标处理.

一个嵌套循环中值不被改变的量叫做循环的全局参数，一些循环的全局参数使下标表达式和循环界只能被非仿射表达式表示.本文设计一种基于动态分析的多面体模型扩展方法，获取程序运行时间时的动态信息，得到导致表达式非仿射的循环的全局参数的具体数值，用定值替代对应的参数，生成循环的全局参数定值化的循环版本，这个循环版本消除了由循环的全局参数引起的非仿射表达式，因而可以形成有效的SCoP.相较于其他的多面体模型非仿射扩展方法，本文的方法识别循环中值不变的全局参数，适用于值特定的循环.

1 研究背景

1.1 SCoP

SCoP的特点是函数体中最大的连续语句集，是步长为常数、循环边界和访存数组下标可以用仿射表达式表示的循环嵌套序列.SCoP中不包含带有副作用的函数调用［3］，即只允许纯函数和常量函数的调用.程序中一个典型的SCoP如图1所示.

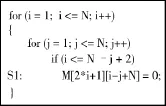
图1 SCoP的一个实例Fig.1 A case of SCoP

1.2 仿射表达式

仿射表达式:Ax+Bn.其中，x表示循环的迭代向量，x=(i1，i2，…，in)T，A，B表示整数向量，A= (x1，x2，…，xn)，B=(xn+1，xn+2，…，xn+k+1)，n表示循环的全局参数向量，n=(n1，n2，…，nk，1)T.例如:对于循环loops(i，j)和参数(m，n)，所有仿射表达式的形式如下:

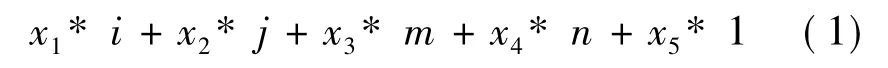
式中，x1，…，x5是整数，形如i*n或者n*m的表达式不允许出现.

2 非仿射的动态扩展方法

2.1 动态优化

动态优化是指分析优化工作要结合程序运行时间时的动态信息进行或者是在程序的运行时间内进行分析优化.在编译时间时，程序中存在一些无法判断是否违反SCoP限制条件的代码区域，为了保证优化的正确性，静态优化技术对其保守估计，不对其进行优化，因此大大降低了可优化代码的覆盖率［3］.在运行时间时，可以获取到程序更多、更准确的信息，因此能对当前区域是否满足SCoP条件做出更准确的判断.很多编译时间时无法判断的代码情况在程序运行中是满足SCoP的限制条件的.因此，在运行时间时检测并记录代码信息，在编译时间时将这些动态信息用于对非仿射的循环界、访存数组下标等代码的并行优化，可以使更多的循环体被优化.

GCC(GNU compiler collection)实现动态优化的方式是在程序第一次运行的编译时间时进行程序插桩，运行时间时插桩程序执行，记录程序运行时的动态信息并反馈给编译器，这些记录的动态信息被称为profile信息.在对程序进行再次编译时，利用收集的动态profile信息，对程序优化，生成优化后的可执行文件.记录profile信息并利用该信息进行优化的过程被称为profile优化过程.

GCC中的value profile优化方法在程序运行时记录变量的值，并统计它每个值的出现次数，如果一个值出现的次数在总次数的一半以上，那么就判定该值可以进行value profile优化，例如将除法运算的除数替换成为一个定值.总得来说，value profile优化基于某个出现概率大的定值增加了一条执行得更快的路径，代价是增大了代码规模.

本文设计的多面体模型表示范围的扩展方法，是基于GCC中的value profile动态优化框架完成的.

2.2 非仿射问题

许多程序的代码存在如图2所示的情况，循环中的循环界或者访存数组下标存在由循环的全局参数引起的非仿射项，使得循环界或者数组下标只能用非仿射表达式表示.例如，C语言不能定义维度大小未知的多维数组，因此经常会使用一维数组来代替多维数组，通过下标的映射公式实现一维数组到多维数组的映射.然而，这种方式产生了非仿射的数组下标.如图2，在编译时间时静态分析，j*N+i被识别为非仿射表达式，因此该循环不能被多面体模型表示，该代码区域无法被并行优化.而在实际的执行过程中，循环的全局参数N往往是一个给定的常数，这样的话j*N+i就可以被转换成可以被多面体模型表示的仿射表达式.

图2 非仿射的数组下标Fig.2 Non-affine array index

2.3 方法设计

本文设计一种方法，基于GCC的value profile动态优化框架，结合在运行时间时循环全局参数的值的信息对多面体模型的表示范围进行非仿射扩展.如图3所示，本文设计的动态非仿射扩展方法主要分为7个步骤来执行.1)代码分析;程序第一次运行时，在编译时间时分析程序，寻找引起非仿射表达式的循环的全局参数，准备记录该变量的profile信息.2)代码插桩;在编译时间时插入代码以在程序运行时间时收集变量的值和出现次数等profile信息.3)收集profile信息;程序第一次运行的运行时间时，记录变量的profile信息.4)分析N值的信息;程序第二次运行时，在编译时间时对变量的profile信息分析，判断该循环全局参数的值是否在大多数执行情况中是定值.5)生成参数定值化的循环版本;经过步骤(4)的分析，如果变量在大多数情况时取同一定值，则用该定值替换变量，生成对应该值的参数定值化的循环版本，在这个循环版本中，由该循环全局参数引起的非仿射情况被去除.6)多面体模型并行优化;GCC编译器中的多面体模型框架识别优化代码区域的SCoP，并对SCoP进行并行优化.由于参数定值化的循环版本去除了原循环中的非仿射表达式，若该循环同时满足SCoP的其他限制条件，则此循环版本可被多面体模型表示优化.7)运行优化程序;经过优化的程序在运行时，即时判断正在运行的函数中循环的全局参数的值是否与编译生成的参数定值化的循环版本匹配，若匹配，则运行优化(并行)版本;若不匹配，则运行原串行版本.

图3 非仿射扩展的执行流程Fig.3 Implementation of the non-affine extensions

本文主要实现第(1)和第(5)步骤，其他几个步骤在value profile框架中已经实现.步骤(1)是对程序进行分析，寻找程序中需要进行value profile的变量，步骤(5)就是对程序进行SCoP的动态非仿射扩展部分的代码优化.

2.4 代码分析

分析当前函数，提取每条语句中的数据引用，分析每个数据引用的下标，分析过程如图4所示.若当前处理的数组下标中存在非仿射乘法项，则对当前乘法项的两个操作数分析，若操作数中存在循环的全局参数，则将该参数放入profile容器中，以待进行后续的处理.

图4 寻找profile值的执行流程Fig.4 Implementation of profiling

2.5 生成优化版本

程序第二次编译时间时对循环进行转换，生成参数定值化的循环版本.它复制当前循环，将进行了profile优化的循环的全局参数替代为定值，生成新的循环版本.并生成条件语句以在程序运行时间时判定执行哪个循环版本.

图5(a)所示为原程序，图5(b)所示为优化后的程序.其中bb1end是指新生成的条件语句，判断在运行时间时真实的循环全局参数的值是否与优化的循环版本中的值匹配，loop_specific_version是指将循环的全局参数用定值替换后的循环版本.

图5 代码转换Fig.5 Code transformation

完成代码转换后，对当前函数的控制流程图进行修改，分离原来的bb块，向流程图中添加新的边.控制流程图的修改过程如图6所示.

3 实 验

3.1 实验指标

实验将通过对比优化前后GCC-4.8.3编译器识别出的SCoP的数目和程序运行的加速比来验证本文方法的有效性.

图6 修改函数流程图Fig.6 Modification of the CFG

(1)如果识别出的SCoP数目变多，就说明本文的方法可以有效地扩展多面体模型的表示范围.

(2)加速比是测试程序的基准运行时间与使用多面体模型编译后程序运行时间的比值.基准时间是指不对程序使用多面体模型优化编译所得程序的运行时间.如果加速比提升，就说明本文的方法可以有效地提高程序的运行速度.

3.2 实验内容

本实验使用GCC-4.8.3编译，使用PolyBench (the Poyhedral Benchmark suite)测试集进行实验，该测试集被广泛应用于多面体模型优化方法的测试中.在处理器为4核，主频为1.8 GHz，内存为1 GB，操作系统为Linux的虚拟机上运行所有的测试集.

分别在GCC-4.8.3和使用本文设计的多面体非仿射扩展方法优化后的GCC-4.8.3上运行该标准测试程序集合，对比实验指标，对实验结果进行分析.每个程序共运行四次，

图7为每次运行的编译选项.图7(a)所示选项为编译器编译程序时，仅使用-O2选项编译，编译所得程序的运行时间作为基准时间;图7(b)所示为使用未经过优化的编译器使用多面体模型编译程序时的选项;图7(c)、(d)为优化后的编译器编译程序时两次运行的选项.其中，-fgraphite选项表示用多面体模型对循环优化，-floop-parallelize-all-ftree-parallelize-loops=4选项表示将可并行化的循环分为4个线程执行.程序第一次运行时，增加-fprofile-generate选项，用以分析程序，找到需要profile的变量，并在程序运行时输出变量的profile信息;程序第二次运行时，增加选项-fprofile-use，利用收集的动态profile信息使用本文设计的方法对程序进行优化.

图7 编译参数Fig.7 Program parameters

3.3 实验结果及分析

对GCC-4.8.3的多面体进行非仿射扩展，优化前后识别出的SCoP数目进行对比，结果如图8所示.可以看出，对于大多数程序，用本文方法优化后的编译器可以识别出更多的SCoP，即有更多的代码区域可以被多面体模型表示.由此说明了本文的方法可以有效地扩展多面体模型的表示范围.

图8 优化前后编译器识别出的SCoP数目比较Fig.8 Comparison of the number of recognized SCoPs

图9显示了编译器在多面体优化前后编译各个测试程序的加速比对比.从图中可见，由于优化后的编译器可以识别出更多的SCoP，多面体可以表示和优化更多的代码区域，在特定的情况下加速比也有了相应的提高.可以看到，程序bicg，gemm，mvt，trisolv适用于本文设计的多面体扩展方法，将这些表达式中的循环参数用定值替换后，可以被多面体模型表示优化，加速比有了明显的提升，gemm的加速比达到了5.7倍，这是因为将循环参数替换为定值后，不仅可以使并行优化应用到更多的代码区域上，同时也可以使一些其他优化有更好的应用.而2mm、3mm等程序，虽然该扩展方法可以识别出更多的SCoP，然而由于这些程序代码中自身存在的依赖关系使得这些程序代码无法被转换成并行代码并行执行，因此加速比并没有提升.对于symm等程序，优化后的编译器可以识别出更多的SCoP，然而它们的加速比却下降了，这并不是由于本文设计的方法增加了选择执行哪个程序版本的路径引起的，因为选择路径的时间耗费非常少，可以忽略不计.这种情况产生的原因是，进行了循环参数定值化转换的循环版本的运行速度确实比原循环版本运行速度慢.

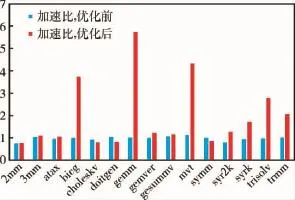
图9 优化前后测试程序执行时间加速比Fig.9 Comparison of the number of speedup

4 结 论

针对代码区域存在由循环参数引起的非仿射的循环界和访存数组下标时不能被并行优化的情况，本文基于动态分析设计了一种针对多面体模型非仿射问题的扩展方法.在程序的运行时间时收集循环参数的动态信息，在编译优化时对这些动态信息进行分析，如果满足条件，则将该循环参数替换为定值，生成非仿射循环的参数定值化的循环版本.通过实验验证，本方法扩展了多面体模型的表示范围，使更多的代码区域可以被优化.本文的方法识别循环中重复出现的循环参数，适用于由循环参数引起的非仿射表达式的情况.

［1］李川，陈朝晖.基于多面体模型的数据依赖分析方法［J］.空间控制技术与应用，2015，41(5):43-47.LI C，CHEN Z H.Data-dependence analysis method based on polyhedral model［J］.Aerospace Control and Application，2015，41(5):43-47.

［2］POP S，COHEN A，BASTOUL C，et al.GRAPHITE: Polyhedral analyses and optimizations for GCC［C］// Proceedings of the 2006 GCC Developers Summit.Ottawa;GCC，2006:179-197

［3］BENABDERRAHMANE M W，P L N，COHEN A，et al.The polyhedral model is more widely applicable than you think［J］.Lecture Notes in Computer Science，2010:283-303.

［4］GRÖßLINGER A.The challenges of non-linear parameters and variables in automatic loop parallelisation［D］.University of Passau，Department of Informatics and Mathematics，2009.

［5］GRÖßLINGER A.Extending the polyhedron model to inequality systems with non-linear parameters using quantifier elimination［D］.University of Passau，Department of Informatics and Mathematics，2003.

［6］BAGHDADI R，COHEN A，BASTOUL C，et al.The potential of synergistic static，dynamic and speculative loop nestoptimizationsforautomatic parallelization［C］//Workshop on Parallel Execution of Sequential Programs on Multi-core Architectures(PESPMA'10)，2010.

［7］JIMBOREAN A，L M，et al.VMAD:an advanced dynamic program analysis＆ instrumentation framework［C］//CC-21st International Conference on Compiler Construction.2012:220-237.

［8］ALEXANDRA J，F D J，JUAN M M C.Dynamic and speculative polyhedral parallelization using compilergenerated skeletons［J］.Springer Science，2013，42 (4):529-545.

［9］ANAND V，M S，MARY H.Non-affine extensions to polyhedral code generation［C］//ACM CGO:Orlando，FL，2014.

A Non-Affine Extension Method of Polyhedral Model Based on Dynamic Analysis

WANG Jianhua，CHEN Zhaohui
(Beijing Institute of Control Engineering，Beijing 100190，China)

The polyhedral model is now only applied in code regions with affine expressions in arrays’indexes.A method is presented that extending polyhedral model to non-affine expression.With the information acknowledged in runtime，non-affine expressions can be transformed to affine expressions，which are led by parameters that do not change in the loop nest.Then a specialized version of the original loop is generated，which makes polyhedral techniques applicable.This method enables the polyhedral model to be applicable in more code regions.More SCoPs in the code regions are recognized and higher speedup is achieved，therefore the performance of the program is improved.The validity and efficiency of the presented method are demonstrated by a series of experiments.

parallel compiling;polyhedral model;SCoP;affine;dynamic analysis

TP31

:A

:1674-1579(2016)02-0057-06

10.3969/j.issn.1674-1579.2016.02.011

王建花(1989—)，女，硕士研究生，研究方向为并行计算;陈朝晖(1969—)，男，研究员，硕士生导师，研究方向为航天嵌入式软件技术.

*国家基础科研资助项目(JCKY2016203B006)

2015-10-21