挠性支承对飞轮隔振系统性能的影响分析*

陈 辰，王 虹，武登云，樊亚洪，关 新

(北京控制工程研究所，北京100190)

挠性支承对飞轮隔振系统性能的影响分析*

陈 辰，王 虹，武登云，樊亚洪，关 新

(北京控制工程研究所，北京100190)

飞轮的高速转子在运转过程中会激发微幅多频振动，对航天器的高精度姿态稳定控制产生不利影响.本文基于飞轮隔振系统结构，建立其动力学模型，并通过实验验证该被动隔振装置的固有模态.对增加挠性支承的飞轮隔振系统的数学模型，通过仿真分析隔振装置在挠性支承条件下对飞轮扰动的抑制效果，实验测试了不同挠性支承条件对飞轮隔振系统微振动特性的影响.结果表明，隔振装置在悬臂挠性支承条件下依然具有优异的隔振性能，挠性支承刚度的适当减弱有利于飞轮隔振系统抑制扰动;挠性支承刚度会降低飞轮隔振系统的二阶结构固有振动频率，但基本不影响其涡动特性.

挠性支承;飞轮;被动隔振;微振动

0 引 言

飞轮是高精度高稳定度航天器上常用的姿态控制执行机构［1］.但由于转子静动不平衡、机械轴承的非理想特性、驱动电机扰动以及挠性结构共振等一系列因素，飞轮工作时会出现持续、大量且频带分布很广的微幅多频振动，通常称为微振动.国内外研究表明，以飞轮为代表的高速旋转惯性执行机构是卫星姿态稳定和精度保持的最大干扰源［2-3］.因此，飞轮微振动抑制成为航天器实现高精度姿态控制的迫切需求.在隔振技术的研究中，隔振方法包括被动隔振、主动隔振和主被动混合隔振.主动隔振装置结构通常较为复杂，由此带来的可靠性问题在一些特殊场合限制了主动隔振系统的应用.而被动隔振方法具有设备简单、易实现、高频隔振效果好等优点，特别是对于可靠性要求较高的场合，被动隔振往往是首选［4］.例如，在哈勃望远镜的飞轮上安装的被动隔振装置，对18～20 Hz的振动起到了优异的隔振效果［5-6］.国内高校和科研机构在飞轮隔振领域也取得了一定的成果，如粘弹性筒形阻尼器，压电式作动器［5］、多杆隔振平台［6］等，但总体而言，基本仍处于结构方案和研究方法探索阶段.飞轮一般通过支架安装在航天器主结构上，支架的动力学特性对飞轮系统的振动响应具有重要影响.

本文针对飞轮微振动问题，基于一种调峰错频隔振原理的被动隔振装置，建立飞轮隔振系统的动力学模型和有限元模型，通过仿真分析和实验验证其固有特性.通过对比三种不同刚度的T形悬臂挠性支架支承飞轮隔振系统微振动特性，分析挠性支承对飞轮隔振系统性能的影响.

1 飞轮隔振系统动力学建模

1.1 动力学方程

飞轮隔振装置，如图1所示单向隔振器由外壳、阻尼器、上端盖、运动导杆及柔性铰、微调弹簧、下端盖及柔性铰构成.

图1 挠性支承飞轮隔振系统结构示意图Fig.1 The structure sketch map of flywheel-isolator system with a flexible bracket

为避免系统共振，隔振装置的固有频率一般在10～20 Hz.隔振装置的阻尼比越小，对高频扰动的衰减性能越好，但共振峰值越高.在固有频率范围内，需要在共振峰放大倍数与高频衰减性能之间进行合理折衷.该隔振装置的固有频率在15 Hz左右，阻尼比为0.1.

选取描述飞轮运动的广义坐标

式中，ux、uy、uz分别为飞轮质心的平动位移量，θα、θβ、θγ为飞轮的3个转角.

假设隔振装置刚度中心C与飞轮质心重合，见图1，作用在飞轮质心处的扰振载荷可表示为fC=［fxfyfzMxMyMz］T，根据拉格朗日方程［7］，可以推导出安装隔振装置后飞轮运动的动力学方程为

质量阵M的表达式为

mw为飞轮的质量，Iwx、Iwz为飞轮的转动惯量，Iry为飞轮转子的转动惯量.

隔振装置对其刚度中心C表现出的刚度阵是一个对角矩阵.刚度阵KCC的表达式为

隔振装置对其刚度中心C的阻尼阵假定为与刚度矩阵具有相同的对角形式.阻尼阵CCC的表达式为

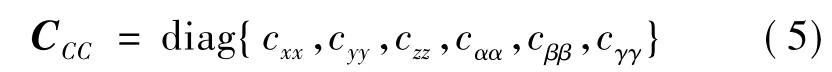
陀螺阵G的表达式为

Iry为飞轮转子的转动惯量，Ω为飞轮转子的转速.

1.2 固有频率实验验证

飞轮系统基本参数见表1，计算得到隔振装置的固有频率如表2所示.

通过表2中的仿真计算结果可知，系统固有频率在9.8～18.8 Hz范围内.对隔振装置采用锤击法获得飞轮隔振装置的传递特性如图2所示.测试结果见表2，实测系统固有频率在11～18.3 Hz范围内，实验结果同仿真结果的误差最大不超过13.7%，验证了系统的固有频率.

表1 飞轮系统基本参数Tab.1 Parameters of the flywheel

表2 飞轮隔振系统各阶频率仿真计算及实验测试结果Tab.2 Resonant frequencies based on the calculation and experiment results of flywheel-isolator system

图2 飞轮隔振系统传递函数实测曲线Fig.2 Transfer function curves of flywheel-isolator system

2 挠性支承飞轮隔振系统扰振动力学建模

2.1 动力学建模

如图1所示，飞轮主要由轮体、角接触球轴承、电机和壳体组成.当飞轮隔振系统与挠性支承固接后，如图1所示的系统会受到来自转子部分的扰动而产生微振动.本文针对图1挠性支承飞轮隔振系统轴向微振动进行建模仿真.

由△(-γ)等效变换方法［8］可以简化计算飞轮内部的轴向刚度.根据挠性支承飞轮隔振系统轴向受力情况，可以将系统简化为如图3所示的轴向质量-弹簧阻尼等效模型.m1为挠性支承和与其固接的隔振装置下平台质量;m2为隔振装置上平台和与其固接的轮体基座、高速主轴、内加载套筒及角接触球轴承的质量;m3为外加载套筒，轴承安装壳和轮体等转子部分的质量.Ky1、Ky2、Ky3分别为挠性支承、隔振装置及飞轮内部各组件的等效刚度，其中，Ky1与图1中的挠性支承悬臂厚度(b)成正比.Cy1、Cy2、Cy3分别为阻尼项.

针对图3建立挠性支承飞轮隔振系统轴向动力学模型如下:

图3 挠性支承飞轮隔振系统轴向等效简化模型Fig.3 Simplified mode of the flywheel-isolator system with a flexible bracket

作为仿真结果对比，对挠性支承飞轮系统进行动力学建模，其模型如下:

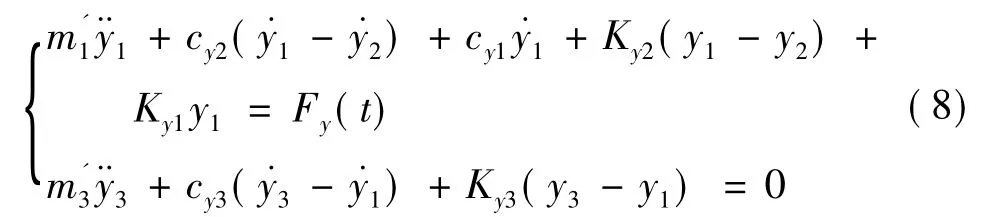
其中:为挠性支承与轮体基座、高速主轴、内加载套筒及角接触球轴承的质量之和;为外加载套筒，轴承安装壳和轮体等转子部分的质量和.Ky1、Ky3分别为挠性支承和飞轮内部各组件的等效刚度.Cy1、Cy3分别为阻尼项.

根据角接触球轴承的结构形式可确定旋转轴承的轴向力波动量为:

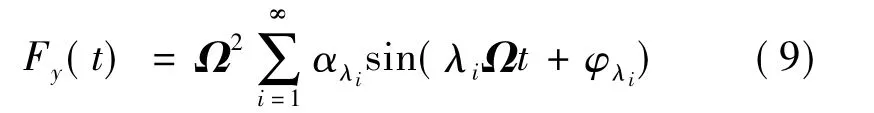
其中，Ω为飞轮转速，αλi为轴承加工相关系数，λi为倍频，φλi为初始相角.由此可计算高速转子质心处的轴向振动位移y2及加装隔振装置前后基座上受到的振动力分别为和

2.2 仿真分析

飞轮系统基本参数见表1，由仿真计算得，Ky1≈2.4×103N/m;经模态实验和轴承的刚度实验等计算［8］可得，Ky2≈50.7 N/m;Ky3≈1.3×107N/m.根据角接触球轴承的结构形式可确定旋转轴承将会激励如下一些倍频成分［8］:保持架旋转频率 λ1= 0.29，滚动体自转频率λ2=1.77，滚动体通过内外圈的频率成分分别为:λ3=3.02，λ4=4.29.通过MATLAB仿真可得12mm挠性支承飞轮系统隔振前、后，其轴向扰振力在5 100 r/min时的频谱图.

通过分析图4可知，85 Hz(f0)为系统工频，加装隔振装置后其振幅大幅减小，振幅衰减率可达90.0%以上.其它频率如20 Hz(0.235f0)，50 Hz (0.588f0)等分别为系统谐振频率，其振幅也均得到了有效抑制.因此，在20～100 Hz的频率范围内该隔振装置应具有良好的隔振效果.

图4 12mm挠性支承飞轮系统隔振前、后Y向扰振力仿真频谱图(5 100 r/min)Fig.4 Simulated spectrum map of axial vibration force of flywheel-isolator system with a 12mm flexible bracket before and after vibration isolation(Y，5 100 r/min)

针对3种不同刚度的挠性支架进行仿真计算，其中，18mm和6mm挠性支承的轴向刚度分别为7.2×103N/m和4.5×102N/m，可得3种挠性支架支承飞轮隔振系统轴向扰振力频谱，见图5所示.

分析图5可知，3种挠性支承飞轮隔振系统的工频均为85 Hz(f0)，而152 Hz(1.79f0)等分别为系统谐振频率.工频为系统主要扰振源，其幅值随挠性支承的挠性增大而减小.其中，6mm挠性支承系统的微振动水平较其它两种挠性支承最低.可见，为了满足飞轮H矢量精度需求，可适当减小挠性支承刚度，以有利于扰振力的抑制.

图5 3种挠性支架支承飞轮隔振系统Y向扰振力仿真频谱图 (5 100 r/min)Fig.5 Simulated spectrum map of axial vibration force of flywheel-isolator system with three kinds of flexible brackets(Y，5 100 r/min)

3 挠性支承飞轮隔振系统实验测试

3.1 实验装置

本实验主要针对挠性支承飞轮隔振系统进行微振动测试，验证仿真结果，分析挠性支承对飞轮隔振系统的影响.

图6为挠性支承飞轮微振动实验测试系统示意图.

图6 挠性支架支承飞轮微振动实验测试系统示意图Fig.6 Scheme of flywheel with a flexible bracket micro-vibration test system

在飞轮坐标系中，Y向为测力台水平长度方向，即飞轮角动量H矢量方向，Z向为测力台水平宽度方向，X向为垂直于测力台台面方向，定义见图6.测试时，控制飞轮转速由0升高至5 100 r/min，持续监测.本文以Y向振动力为代表进行分析.

加装隔振装置后，挠性支承飞轮隔振系统如图7所示，挠性支承通过螺钉固接于测力台，实验中持续监测飞轮升速过程(0→5 100 r/min)的微振动情况.

图7 挠性支承飞轮隔振系统原理样机实物图Fig.7 Physical map of flywheel-isolator system with a flexible bracket

3.2 隔振性能测试

隔振前、后飞轮微振动轴向扰振力频谱如图8所示，通过对比仿真图4可知，仿真图中扰振力曲线与实测曲线基本吻合各扰振力幅值均大幅衰减，其中，系统工频振幅衰减率可达98.0%.

图8 12mm挠性支架支承飞轮隔振前后升速过程Y向扰振力实测频谱图(5 100 r/min)Fig.8 Tested spectrum map of axial vibration force of flywheel with 12mm flexible bracket before and after vibration isolation(Y，5 100 r/min)

3.3 挠性支承影响分析

考查不同刚度挠性支承对飞轮隔振系统的影响，图9给出3种挠性支架支承飞轮隔振系统轴向扰振力频谱图.可以看出，挠性支承刚度适当减弱有利于飞轮隔振系统抑制扰动.通过对比仿真频谱图5可知，等效简化模型仿真结果基本覆盖了实测图中表现出来的主要扰振成分.为了能较为全面分析挠性支承对飞轮隔振系统的影响，还需要对扰振力三维瀑布图进行分析.

图9 3种挠性支架支承飞轮隔振系统Y向扰振力实测频谱图(5 100 r/min)Fig.9 Tested spectrum map of axial vibration force of flywheel-isolator system with three kinds of flexible brackets(Y，5 100 r/min)

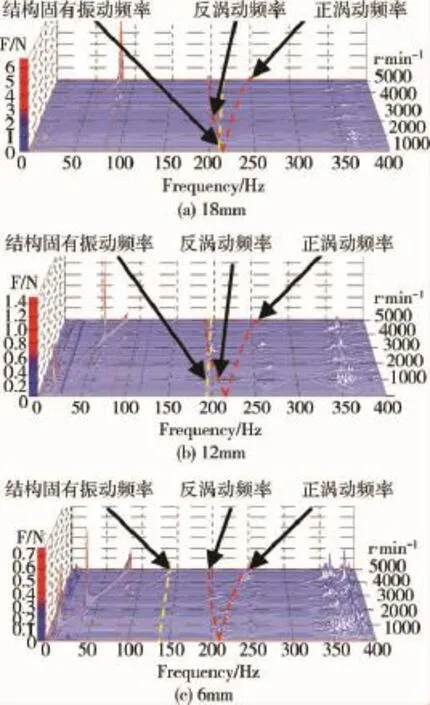
图10 3种挠性支架支承飞轮隔振系统升速过程Y向扰振力瀑布图(0→5 100 r/min)Fig.10 Waterfalls of axial vibration force of flywheel-isolator system with three kinds of flexible brackets(Y，0→5 100 r/min)

图10给出3种挠性支架支承飞轮隔振系统升速过程Y向扰振力三维瀑布图(0～400 Hz).对于挠性支承飞轮隔振系统，其共振频率均在15 Hz左右，系统二阶结构固有振动频率随挠性支承刚度减小而降低，分别为212 Hz(18mm)、196 Hz(12mm)、140 Hz(6mm)，正、反涡动起始频率均为215 Hz，说明挠性支承刚度影响飞轮隔振系统的结构固有振动频率，但基本不影响其涡动特性.这是因为隔振装置的刚度远低于挠性支承，因此正、反涡动频率主要由转子系统和隔振装置的刚度特性决定.

4 结 论

挠性支承条件下飞轮隔振装置具有优异的隔振效果.隔振后系统扰振力振幅显著下降，系统工频成功避开正、反涡动频率，不存在两者的共振放大.挠性支承飞轮隔振系统的隔振性能和微振动特性主要由挠性支承、隔振装置和飞轮组成的振动系统的共振特性决定.适当减弱挠性支承刚度有利于飞轮隔振系统抑制扰动.为取得最佳隔振效果，在设计时须考虑三者共振后的振动特性调整挠性支承的刚度，使整个系统的固有频率尽量避开原有的正、反涡动频率，从而尽可能降低系统的微振动水平.

［1］HYDE TT，HA K Q，JOHNSTON J D，et al.Integrated modeling activities for the James Webb Space Telescope:optical jitter analysis［C］//Proceedings of SPIE Vol.5487.Bellingham，WA:SPIE，2004:588-599.

［2］ELIAS L M，MILLER D W.A coupled disturbance analysis method using dynamic mass measurement techniques［C］//AIAA-2002—1252，Denver，Co.:43rd AIAA/ASME/ASCE/AHS/ASC Structures，Dynamics and Materials Conference.Washington DC:AIAA，2002.

［3］MASTERSON R A，Miller D W.Development and validation of empirical and analytical reaction wheel disturbance models［D］.Cambridge:Department of Mechanical Engineering，Massachusetts Institute of Technology，1999.

［4］郑钢铁.空间飞行器隔振与振动抑制研究进展［C］.第九届全国振动理论及应用学术会议论文集，2007: 8-5.ZHENG G T.Advances in Spacecraft Vibration Isolation and Attenuation［C］//The 9thNational Conference on Vibration Theory and Application，2007:8-5.

［5］GIAIME J，SAHA P，SHOEMAKER D，et al.A passive vibration isolation stack for LIGO:design，modeling，and testing［J］.Review of scientific instruments，1996，67(1):208-214.

［6］BEALS G A，GRUM R C，DOUGHERTY H J，et al.Hubble Space Telescope precision pointing control system［J］.Journal of Guidance，Control，and Dynamics，1998，11(2):119-123.

［7］关新.高分辨率遥感卫星隔振与姿态控制一体化设计［D］.北京:清华大学，2012.GUAN X.Integrated design of vibration isolation and attitude control for high resolution remote sensing satellites［D］.Beijing:Tsinghua University，2012.

［8］罗睿智，虎刚，王全武.基于△-(γ)等效变换的SGCMG高速转子轴向振动特性分析及验证［J］.空间控制技术与应用，2011，37(2):14-20.LUO R Z，HU G，WANG Q W.Axial vibration analysis and validity of high-speed rotor of cantilever SGCMG based on a triangle-star equivalent transformation［J］.Aerospace Control and Application，2011 37(2):14-20.

Effects of the Flexible Brackets on Flywheel Isolation System

CHEN Chen，WANG Hong，WU Dengyun，FAN Yahong，GUAN Xin
(Beijing Institute of Control Engineering，Beijing 100190，China)

The micro-amplitude and multi-frequency vibrations can make the system unable to meet the requirements for the attitude precision and stability，which are produced by the high-speed rotor operation in flywheels installed on the spacecraft.Based on the structure of flywheel isolation system，a natural property of the isolator is validated.For the flywheel isolation system with a flexible bracket，a mathematical model is established.The effects on the characteristics of flywheel micro-vibration are studied，The research results show that the isolator presents a superior property on vibration isolation.The decrease of stiffness of the flexible bracket can help flywheel isolation system suppress the vibrations.The stiffness of flexible bracket can reduce the second order of the system natural vibration frequency，but almost has no effects on the whirl characteristics.

flexible bracket;flywheel;passive isolation;micro-vibration

V414.3+3

:A

:1674-1579(2016)02-0032-06

10.3969/j.issn.1674-1579.2016.02.006

陈 辰(1987—)，男，硕士研究生，研究方向为航天器惯性执行机构;王 虹(1981—)，女，工程师，研究方向为空间惯性执行机构的微振动分析和抑制技术;武登云(1974—)，男，研究员，研究方向为惯性执行机构设计;樊亚洪(1973—)，男，高级工程师，研究方向为磁悬浮惯性执行机构控制;关 新(1986—)，男，高级工程师，研究方向为航天器动力学与控制.

*国家自然科学基金资助项目(51405015和61503015).

2015-09-28