例谈教学设计有效性的实施
■广东省深圳市观澜中学 万 忠
例谈教学设计有效性的实施
■广东省深圳市观澜中学万忠
众所周知,数学课堂教学的有效性与很多方面有着密切的关系,诸如:教师对知识的理解、对学生学情的认知、对所教知识的设计、对学生参与的指导等.新课程教学理念一直致力于课堂教学更需要有效性、高效性,将学习的方式方法进行传授、知识形成过程的理解作为教学的第一原则,而非传统一味的通过训练理解概念、理解数学.那么教学设计的有效性更关注哪些方面呢?按照人教版主编章建跃博士的见解:数学教学设计是一门学问,翻看教材,我们发现数学知识更多的是以形式化的方式存在,这些知识只是一种呈现,并没有让学生直接可以通俗易懂地理解.因此,教学设计的作用恰是在于将冰冷的数学知识转化为可阅读、可理解、可吸收的方式进行学习,这就是教学设计的有效性.
笔者以为,这些描述恰恰对为什么要做好教学设计合理性给予了说明.那么有效性具体落实到课堂教学中去,这种设计是如何实施的呢?主要还是从三点去落实这种设计:第一,教学设计是否尊崇新课程教学的理念,通俗的说,即从做中学,现阶段一线教学的我们也发现,完全放手让学生探究是一种理想化的教学方式,并不切合中学教学的实际,但是在教师设计下的合理探究、启发讲授是将传统教学的方式向前推进了一大步,是可取的、是符合新课程理念的;第二,最近发展区的设计原则,无论是知识难易程度如何,教师设计的准则依旧紧紧围绕最近发展区理论,特殊到一般、感性到理性、具体到抽象都是这一原则的一种具体表象;第三,设计需要贯穿数学思想方法,数学知识是一种静止的、独立的存在,但是教师的教学设计不能使其单一的存在,而需要将其背后隐藏的数学思想方法挖掘出来、展示出来,如代数问题是否有图形化的思考角度、图形问题的缺陷是否有代数统一的方式方法给以回应等.笔者结合“基本不等式”第一课时的设计来谈谈如何去实施落实上述方面,与大家交流.
一、引入的设计
引入是中学数学新知教学必备的环节,引入可以是具体的、抽象的,这需要教师做设计时充分考虑学生的学情,一般程度越好的学生引入可以更为抽象、形式化,反之则以感性的、非形式化更好.以基本不等式第一课时为例,引入设计见下表.

具体化的情境引入 抽象化的一般介绍问题:老王绕一面墙围一块菜地,现有篱笆100米,问:围长、宽各多少时种菜效益可以最大?重要不等式:一般地,如果a,b∈R,那么a2+b2≥2ab(当且仅当a=b时等号成立).(请学生简单地证明)意图:来源自生活情境的设计,更有其研究的价值,学生更能体会基本不等式无处不在的生活价值,这种设计更受学生欢迎.意图:从形式化的角度来说,基本不等式是非常简捷的式子,教师可以直接引入,但是这一数学式的意义何在?有何用处?学生比较茫然.说明:通过引入的简单对比,我们发现,中学数学新知教学一般都是可以追溯到数学的生活情境,这种简单的生活情境看似容易,却在向学生暗示为什么要学基本不等式?学数学之用在哪里?这些没有具体化的情境是难以向中学生渗透的,因此教学设计引入还是建议要有生活的味道.
二、深化的认识
设计意图:由不等式a2+b2≥2ab通过代换得到基本不等式,反映出a、b的任意性.
三、证明的设计
基本不等式的证明并不是本课的难点,但是基于正确性的认识,必须给出证明环节.教师在这一环节中,恰如其分地将最近发展区理论设计到教学中,以合理的证明思路、学生能够思考的环节步步设计,并将证明的常用方式方法给以呈现:
(1)用分析法证明:
显然,④是成立的.当且仅当a=b时,④中的等号成立.
(2)用综合法证明:
设计意图:初步了解分析法证明不等式的一般思路和步骤,培养学生严谨的数学态度和分析问题的一般方法.
四、思想的渗透
1.圆的模型
如图1,AB是圆O的直径,点C是AB上一点,AC=a,BC=b.过点C作垂直于AB的弦DE,连接AD,BD.根据射影定理可得由于Rt△COD中直角边CD<斜边OD,于是有,当且仅当点C与圆心O重合,即a=b时等号成立.
2.“风车”模型
(当且仅当a=b时,等号成立)

图2
设计意图:从不同的侧面理解不等式的实质,进一步加强数形结合的意识,提升思维的灵活性.
五、练习与小结
1.练习的设计
设计意图:借助课堂练习熟悉基本不等式,利用不等式的证明来培养学生严谨的理性精神和数学习惯.
2.小结的设计
(1)重要不等式:若a,b∈R,则a2+b2≥2ab(当且仅当a=b时,等号成立).
(2)基本不等式:若a,b∈R+,则(当且仅当a=b时,等号成立)
(3)注意两个不等式的联系与区别,以及它们的几何解释(数形结合思想).
设计意图:总结梳理本节课所学的内容,使学生形成系统的认识,培养学生的归纳总结能力.
六、思考的设计
(1)如图3,点C是AB上一点,设AC=a,BC=b,CD⊥AB交圆O上半圆于点D,过点C作CE⊥OD于点E,请你利用DC≥DE写出一个含有a、b的不等式,说明何时等号成立.

图3
(2)如图4,点C是AB上一点,设AC=a,BC=b,OF⊥AB交圆O上半圆于点F,请你利用FC≥OF写出一个含有a、b的不等式,说明何时等号成立.

图4
设计意图:借助课后作业了解另外两个不等式的几何解释,加强数形结合的意识,提升数学的兴趣和思维的灵活性.
综上,从上述“基本不等式”第一课时设计来看,笔者在证明环节给予了学生动手的尝试,这种尝试证明是在教师设计好分析法和综合法的步骤下填空进行,是一种有效的可操作.另一方面来说,对于学生从理解基本不等式到进行简单的运用,这种基于最近发展区的解决思维逻辑,时时刻刻体现在教师对于本课的设计之中.
从教师对于本课的思想方法体现在了数形结合思想,基本不等式是代数知识,教师将这种代数知识以几何方式充分地展示了,结合图形的设计教学,在不知不觉中将以形辅数的想法进行了渗透.总之,从数学教学的有效性来看,围绕知识点进行的设计需要从多方面来思考,笔者从三方面进行了一堂课的设计,这些方面在体现教学设计有效性的同时,还存在着多处不足,如:学生的探索是否可以更多?学生的建构合理与否?学生的积极性能否真正被调动?很多的思考还需进一步完善,以本文初步的思考,恳请读者给出更进一步指正.
参考文献:
1.杨玉东,范文贵.高中数学新课程理念与实施[M].海口:海南出版社,2011.
2.柴贤亭.数学教学中的问题设计[J].教学与管理,2012(10).
3.沈恒.浅谈中学数学课堂教学的适度形式化[J].中小学数学,2010(5).F
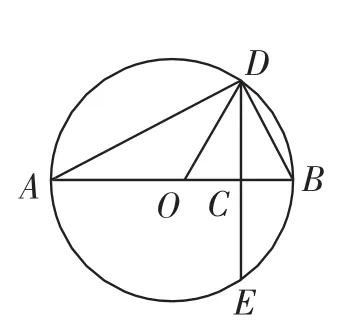
图1

