高中数学教材“推广型”内容的教学策略

■江苏省栟茶中学　缪瑞红



高中数学教材“推广型”内容的教学策略

■江苏省栟茶中学缪瑞红

一、“推广型”内容的教学面临的问题

1.推广的重要性

要认识到推广的重要性问题，就是要回答“数学推广的原因是什么”.在教学过程中，教师需要立足于学生的实际认知能力，并糅合数学发展及逻辑规律，使学生深入意识到推广的重要性.举个例子，在讲述大于360°的角及负角时，就能列出学生在实际生活中常见到的大于360°的角和负角，比如翻单杠时的转体动作、跳水时翻腾的动作、钟表内的指针转动、车轮的转动等形成的各种角度，以期表现出创新推广的必要性和重要性，同时也让学生更好地感受到数学的魅力和价值.

2.推广的策略性

面对推广的策略性问题，就是要回答“怎样更好地做到推广”.综合数学的学习思考、探究研讨的过程，往往应用如图1所示的思维模式.

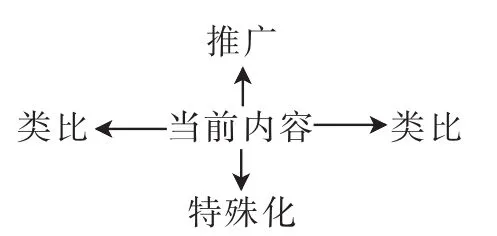
图1

在推广过程中，为了明显展示相联系的概念，可以用类比、归纳、转化及化归等思维方式，能够有效地推动学生进行数学思考，让他们更快速地了解到自己的兴趣所在，并能在学习过程中得到探究方法的道理.比如，在讲解平面几何中的向量方法时，教师可以用这样的“关系图”，如图2所示.

图2

3.推广的应用性

面对此问题时，就是要回答“实施推广后的作用是什么”.教师应该立足于旧概念推广获取新概念的根本上，看重新概念或知识的实践，使推广的意义更好地体现出来.此意义，不单单显示在新知识对旧知识的革新上，更能使学生体验到数学概念的推广会创造更优质繁多的性质.举例来说，我们把勾股定理推广到余弦定理后，就能提出此类问题：在解决三角形问题中，如果∠C是锐角的话，那么可以得出a2+b2＞c2；如果∠C是钝角的话，那么a2+b2＜c2.按这样的方式，不仅使学生充分了解到余弦定理与勾股定理的联系，还可以使学生体验到新概念创造的意义.

二、“推广型”内容的教学的有效策略

1.筹建具备认知冲突的实际情境，展现推广的重要性

通过一定的认知冲突可以激发学生的好奇心理，来吸引学生进行关注和思考.认知冲突是进行数学教学的高效时机.在推广教学的过程中，筹建具备认知冲突的实际情境，可以更好地展现推广的重要性.

（1）使教学情境贴近生活，提高推广的必要性.在处理实践生活和生产实际等相关问题时，实施数学推广一般是最为科学有效的手段.因此教师糅合生产生活的实际实例来筹建教学场景，让新概念的产生更有说服力.

案例1在对“抛物线”这堂课进行讲解时，老师可以先根据抛物线的定义，对同学提出问题，接下来推广其解题技巧.

例1过抛物焦点F的直线与抛物线交于A、B两点，若A、B在抛物线准线上的射影分别为A1、B1，则∠A1FB1的度数是多少？

如图3，抛物线的定义是：在平面内，到一个定点O和一条直线l的距离相等的点的轨迹，叫做抛物线.老师在引导学生对抛物线学习的同时，还可以将其类比推广，A1、B两点之间的连线是否经过点O或∠A1OB1的度数是多少？

图3

（2）让事物之间的关系变得普遍，展示推广必要性.在推广中，一般方法是将变量或物体之间的特殊关系变成普通关系，以此来得到具备普遍意义的概念和公式.在教学过程中，通常先回顾涵盖范围小或概括能力弱的知识，然后以此为前提筹建有认知冲突的教学情境.举例来说，在把函数的图形对称推广到如何判断函数的奇偶性，在认知系统发展的基础上说，应归为“下、上位关系学习”一类，“先行组织者”表示函数奇偶性的判定.在课堂教学中，教师能够设立下面的情境.

案例2教师在进行讲解“函数的奇偶性”一课时，其中书本是这样定义函数的奇偶性：一般地，先设函数y=f（x）的定义域为A，如果对于任意的x∈A，都有f（-x）= f（x），那么称y=f（x）是偶函数；如果对于任意的x∈A，都有f（-x）=-f（x），那么称函数为奇函数.教师可以先要求学生进行自学，结合一些具体形象的函数画出图像，从而总结出奇函数与偶函数的概念.

其实老师可以对函数奇偶性这个概念做进一步的推广，如果对于任意的x∈A，都有f（-x）=f（x），实际上就说明有x就有-x存在，这个其实是相对的，也就是定义域是关于原点对称的.所以，通过对定义的推广，我们能够从三个方面来对函数的性质进行判断：首先，判断定义域，看函数的定义域是否是关于原点对称的；其次，判断f（-x）与f（x）之间的关系；最后，若f（-x）=f（x），则可以判断函数y=f（x）是偶函数，若f（-x）=-f（x），则判断函数y= f（x）为奇函数.

2.对已学的知识进行推广探索，加深理解

教育的方法在逐年地随着思想的进步而改变，例如，新提倡的四个方面——知识体系、技能体系、方法体系和经验体系，就已经很大程度上突破了传统的限制，这些方面上的要求，是对普通教育方法的延伸，要求学生不仅能够掌握知识本身，还要能够学以致用，学会自我思考总结，自我提升，并且要能够将所学的知识应用到实际的生活当中，在应用知识的同时，同样能够温故而知新，有新的感悟和收获.下面将简单的介绍几种分析的常规方法：

（1）类比的方法.在数学学习的学业生涯当中，很多的同学都应该对这种方法有比较深的感悟，即从已知到未知的一种探索，很多的知识都是我们已经学习过的，他们往往具有一定的规律和常规性的思维方法，我们受到启迪，从这些已知的东西和思考的角度去解决未知的问题，往往也是十分容易的.

（2）化归的方法.简单的说便是从一个很小的问题得出结论的基础之上，总结得出类似于这个小问题的解决大问题的方法，首先便需要我们能够大胆地去假设，再运用所学的知识对这些假设的思想和结论进行证明演示，假如我们能够证实这些推论是有效的，则能够下定最终的结论了.数学的海洋中，也需要我们敢于假设，往往能够去开辟出新的天地.

3.结论的实用性，掌握类似的方法

我们通过已知的知识进行转化，能够延伸出许许多多新的结论，而这些结论，也能够被我们当成新的定理运用，但是这些定理往往也会具有自身的约束，因此要求我们在得到新的知识之后，还要进行深入的分析和学习，这样不仅能够加深我们对知识的理解程度，也能够让我们养成深入思考的好习惯.

同时在另一个层面上，也要求了老师必须正确地引导学生进行分析.比如说运用辨析的方法，来加深学生理解问题的深度也是十分必要的.

案例3高中数学课本“基本不等式的证明”一节中，对该知识点进行推广.

在训练中可以培养学生多角度思考问题的能力，从而能够灵活多变，不再是死做题，做死题.教育的目标便是培养应变性的人才，懂得思考和会思考才是我们的最终目的，而不是死记硬背，这也是数学学习与其他科目学习的最本质上的区别所在.

三、结束语

类似于这种教学的方法还有很多，帮助学生更加全面地理解知识的无局限性，多样化和运用的广泛性.从小就培养他们在自己有限的知识体系下，能够独立地探究未知的知识，并且加以证实和探讨.不仅要学会思考，还要懂得应用.同时我们也相信，在探索前进的道路上，能够激发学生对于数学奥秘的探索兴趣，以便于更好地学习.

参考文献：

1.曾荣.高中数学教材“推广型”内容的教学策略［J］.教学与管理，2015（7）.

2.晏玲友.高中“数学文化”内容的教学策略研究［D］.重庆：西南大学，2011.

3.符白陵.高中数学函数的教学策略研究［D］.海口：海南师范大学，2014.F